Giải câu 5 trang 101 sách phát triển năng lực toán 9 tập 1
5. Cho đường tròn tâm O, đường kính AB = 30cm. Dây CD có độ dài 24cm vuông góc với AB tại H (hình 3.8).
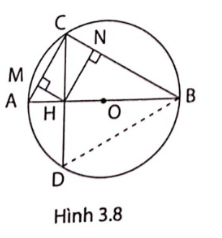
a, Tính độ dài đoạn thẳng HA, HB.
b, Gọi M, N lần lượt là hình chiếu của H trên CA và CB. Tính diện tích tứ giác CMHN.
c, Để tam giác CDB đều thì độ dài dây CD là bao nhiêu? Trình bày lời giải của em.
d, Để tam giác CBA có diện tích lớn nhất thì độ dài dây CD là bao nhiêu? Trình bày lời giải của em.
a, CD vuông góc với AB tại H => HC = HD = $\frac{CD}{2}$ = 12 cm
OB = OC = OA = $\frac{AB}{2}$ = 15 cm
OH = $\sqrt{OC^{2}-CH^{2}}=\sqrt{15^{2}-12^{2}}=9$ (cm)
HA = OA - OH = 15 - 9 = 6 (cm)
HB = OB + OH = 15 + 9 = 24 (cm)
b, CB = $\sqrt{HC^{2}+HB^{2}}=\sqrt{12^{2}+24^{2}}=12\sqrt{5}$ (cm)
AC = $\sqrt{HC^{2}+HA^{2}}=\sqrt{12^{2}+6^{2}}=6\sqrt{5}$ (cm)
Xét tam giác vuông HCB vuông tại H có HN là đường cao => HN.CB = CH.HB
<=> HN.$12\sqrt{5}$ = 12.24 <=> HN = 4,8$\sqrt{5}$
Xét tam giác CHA vuông tại H có HM là đường cao => HM.AC = AH.HC
<=> HM.$6\sqrt{5}$ = 6.12 <=> HM = 2,4$\sqrt{5}$
Xét tam giác ACB có :
- CO là trung tuyến ứng với cạnh AB
- CO = $\frac{AB}{2}$
=> Tam giác ACB vuông tại C (Tính chất đườn trung tuyến của tam giác vuông)
Xét tứ giác CMHN có ba góc vuông là góc $\widehat{HMC}$; $\widehat{HNC}$ và $\widehat{MCN}$
=> CMHN là hình chữ nhật
SCMHN = HM.HN = 4,8$\sqrt{5}$.2,4$\sqrt{5}$ = 57,6 (cm$^{2}$)
c, BCD là tam tam giác đều => BH là trung tuyến của tam giác BCD ứng với cạnh CD và O là giao của ba đường trung tuyến của tam giác ABC
=> OB = $\frac{2}{3}$.HB
Ta có SBCD = $\frac{1}{2}$.HB.CD = $\frac{1}{2}$.CB.DB.sin$60^{0}$
=> HB = CD.sin$60^{0}$
=> OB = $\frac{2}{3}$.CD.sin$60^{0}$
=> CD = $\frac{3OB}{2.sin60^{0}}$ = $\frac{3.15}{2.\frac{\sqrt{3}}{2}}$ = $15\sqrt{3}\approx 26$ (cm)
d, SCAB = $\frac{1}{2}$.CH.AB
AB là cố định để SCAB là lớn nhất thì CH là lớn nhất
CH lớn nhất khi CH = R hay CD = 2R
Vậy để SCAB là lớn nhất thì CD = 2R = 30 (cm)
Giải những bài tập khác
Giải bài tập những môn khác
Môn học lớp 9 KNTT
5 phút giải toán 9 KNTT
5 phút soạn bài văn 9 KNTT
Văn mẫu 9 kết nối tri thức
5 phút giải KHTN 9 KNTT
5 phút giải lịch sử 9 KNTT
5 phút giải địa lí 9 KNTT
5 phút giải hướng nghiệp 9 KNTT
5 phút giải lắp mạng điện 9 KNTT
5 phút giải trồng trọt 9 KNTT
5 phút giải CN thực phẩm 9 KNTT
5 phút giải tin học 9 KNTT
5 phút giải GDCD 9 KNTT
5 phút giải HĐTN 9 KNTT
Môn học lớp 9 CTST
5 phút giải toán 9 CTST
5 phút soạn bài văn 9 CTST
Văn mẫu 9 chân trời sáng tạo
5 phút giải KHTN 9 CTST
5 phút giải lịch sử 9 CTST
5 phút giải địa lí 9 CTST
5 phút giải hướng nghiệp 9 CTST
5 phút giải lắp mạng điện 9 CTST
5 phút giải cắt may 9 CTST
5 phút giải nông nghiệp 9 CTST
5 phút giải tin học 9 CTST
5 phút giải GDCD 9 CTST
5 phút giải HĐTN 9 bản 1 CTST
5 phút giải HĐTN 9 bản 2 CTST
Môn học lớp 9 cánh diều
5 phút giải toán 9 CD
5 phút soạn bài văn 9 CD
Văn mẫu 9 cánh diều
5 phút giải KHTN 9 CD
5 phút giải lịch sử 9 CD
5 phút giải địa lí 9 CD
5 phút giải hướng nghiệp 9 CD
5 phút giải lắp mạng điện 9 CD
5 phút giải trồng trọt 9 CD
5 phút giải CN thực phẩm 9 CD
5 phút giải tin học 9 CD
5 phút giải GDCD 9 CD
5 phút giải HĐTN 9 CD
Trắc nghiệm 9 Kết nối tri thức
Trắc nghiệm 9 Chân trời sáng tạo
Trắc nghiệm 9 Cánh diều
Tài liệu lớp 9
Văn mẫu lớp 9
Đề thi lên 10 Toán
Đề thi môn Hóa 9
Đề thi môn Địa lớp 9
Đề thi môn vật lí 9
Tập bản đồ địa lí 9
Ôn toán 9 lên 10
Ôn Ngữ văn 9 lên 10
Ôn Tiếng Anh 9 lên 10
Đề thi lên 10 chuyên Toán
Chuyên đề ôn tập Hóa 9
Chuyên đề ôn tập Sử lớp 9
Chuyên đề toán 9
Chuyên đề Địa Lý 9
Phát triển năng lực toán 9 tập 1
Bài tập phát triển năng lực toán 9

Bình luận