Bài tập dạng Đường trung tuyến - Đường cao - Đường phân giác của tam giác

Bài tập 1:

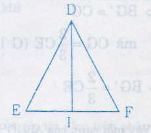
a) $\Delta DEI  = \Delta DFI$ có:

DI là cạnh chung

DE = DF ( $\Delta DEF$ cân)

IE = IF (DI là trung tuyến)

Nên $\Delta DEI  = \Delta DFI$ (c.c.c)

b) I là trung điểm của  EF nên IE = IF = 5cm

$\Delta DEI$ vuông tại I nên $DI^{2} = DE^{2} – EI^{2}$ (định lí pytago)

$\Rightarrow  DI = 12$

Bài tập 2: 

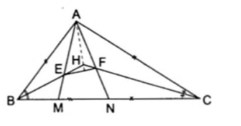
Góc $\widehat{A}$ tù, nên BC lớn hơn AB và AC. Vậy M nằm giữa hai điểm B và C.

Mặt khác, $\Delta ABN$ có BN = BA nên $\Delta ABN $cân tại B.

Vậy BE là tia phân giác $\widehat{B}$, đồng thời cũng là đường cao nên $BE \perp AN$

$\Delta ACM$ có CA = CM nên $\Delta ACM$ cân tại C $\Rightarrow$ CF là tia phân giác $\widehat{C}$ và cũng là đường cao. $\Rightarrow  CF \perp AM$

$\Delta AEF$ có $BE \perp AN$ và $CF \perp AM$

Gọi H là giao điểm của BE và CF nên $AH\perp  EF$ (tính chất ba đường cao trong tam giác)

Bài tập 3: 

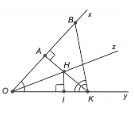
a) Vì H nằm trên đường phân giác của $\widehat{xOy}$ nên H cách đều Ox, Oy nên AH = HI

b) $\Delta AOH$ vuông tại A, nên $AH =\sqrt{5^{2}-3^{2}}=4$

Ta có H là giao điểm của ba đường phân giác của $\Delta OBK$ nên H cách đều ba cạnh của tam giác đó

Vậy khoảng cách từ điểm H đến BK bằng AH = 4 cm