Câu 1: Trong các phương trình sau, cặp phương trình nào tương đương?

• A. x = 1 và x( x - 1 ) = 0

• B. x - 2 = 0 và 2x - 4 = 0

• C. 5x = 0 và 2x - 1 = 0
• D. $x^{2}-4$ = 0 và 2x - 2 = 0

Câu 2: Giá trị của m để phương trình 2x = m + 1 có nghiệm x = - 1 là ?

• A. m = 3.   
• B. m = 1.

• C. m = - 3   

• D. m = 2.

Câu 3: Cho a + 1 ≤ b + 2. So sánh hai số 2a + 2 và 2b + 4 nào dưới đây đúng ?

• A. 2a + 2 > 2b + 4
• B. 2a + 2 < 2b + 4

• C. 2a + 2 ≤ 2b + 4

• D. 2a + 2 ≥ 2b + 4

Câu 4: Một tổ sản xuất theo kế hoạch mỗi ngày phải sản xuất 50 sản phầm. Khi thực hiện tổ đã sản xuất được 57 sản phẩm một ngày. Do đó hoàn thành trước kế hoạch 1 ngày và còn vượt mức 13 sản phẩm. Hỏi theo kế hoạch tổ phải sản xuất bao nhiêu sản phẩm? 

• A. 550                              
• B. 400                         
• C. 600                              

• D. 500

Câu 5: Cho các đoạn thẳng AB = 6cm, CD = 4cm, PQ = 8cm, EF = 10cm, MN = 25mm, RS = 15mm. Hãy chọn phát biểu đúng trong các phát biểu sau?

• A. Đoạn AB và PQ tỉ lệ với hai đoạn thẳng EF vs RS.

• B. Hai đoạn thẳng AB và RS tỉ lệ với hai đoạn thẳng EF và MN.

• C. Hai đoạn thẳng AB và CD tỉ lệ với hai đoạn thẳng PQ và EF
• D. Cả 3 phát biểu đều sai.

Câu 6: Cho a ≥ b. Khẳng định nào sau đây đúng?

• A. 2a - 5 ≤ 2 b - 1)
• B. 2a - 5 ≥ 2(b - 1)

• C. 2a - 5 ≥ 2(b - 3)

• D. 2a - 5 ≤ 2(b - 3)

Câu 7: So sánh m và $m^{2}$ với 0 < m < 1.

• A. $m^{2}$ > m

• B. $m^{2}$ < m

• C. $m^{2}$ ≥ m
• D. $m^{2}$ ≤ m

Câu 8: Chọn câu trả lời đúng: Cho hình bên, biết DE // AC, tìm x:

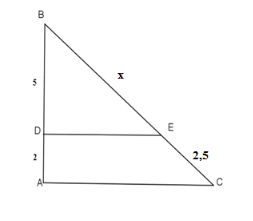
• A. x = 6, 5       

• B. x = 6, 25       

• C. x = 5 
• D. x = 8        

Câu 9: Nghiệm của phương trình $2x(x+1)=x^{2}-1 $ là?

• A. x = - 1.   

• B. x = ± 1.
• C. x = 1.   
• D. x = 0.

Câu 10: Cho tam giác ABC vuông tại A có AB = 6, AC = 8. Tia phân giác góc Bˆ cắt AC tại D. Độ dài AD là:  

• A. 1,5 

• B. 3

• C. 4,5
• D. 4

Câu 11: Tam giác có: ABC, Aˆ=2Bˆ, AC = 16 cm, BC = 20 cm. Tính độ dài cạnh AB.

• A. 18 cm 
• B. 20 cm
• C. 15 cm 

• D. 9 cm

Câu 12: Một người đo chiều cao của cây nhờ 1 cọc chôn xuống đất, cọc cao 2,45 m và đặt xa cây 1,36 m. Sau khi người ấy lùi ra xa cách cọc 0,64 m thì người ấy nhìn thấy đầu cọc và đỉnh cây cùng nằm trên một đường thẳng. Hỏi cây cao bao nhiêu? Biết khoảng cách từ chân đến mắt người ấy là 1,65 m.

• A. 4, 51 m      
• B. 5, 14 m      
• C. 5, 41 m      

• D. 4, 15 m

Câu 13: Cho tam giác ABC có BC = 8cm; BH và CK (H ∈ AB; K ∈ AC) là hai đường trung tuyến kẻ từ B và C (H ∈ AB; K ∈ AC). Tính độ dài đoạn HK.

• A. HK = 2 cm

• B. HK = 4 cm

• C. HK = 6 cm           
• D. HK = 8 cm

Câu 14: Hãy chọn câu đúng. Điều kiện xác định của phương trình $\frac{x}{x-2}-\frac{2x}{x^{2}-1}$ là

• A. x ≠ −1; x ≠ −2
• B. x ≠ 0

• C. x ≠ 2 và x ≠ ±1.            

• D. x ≠ −2; x ≠ 1

Câu 15: Số nguyên lớn nhất thoả mãn bất phương trình $x-\frac{x+5}{2}\leq \frac{x+4}{6}-\frac{x-2}{2}$ là:

• A. -5

• B. 6
• C. -6 
• D. 5

Câu 16: Cho hình hộp chữ nhật ABCD.A'B'C'D' có diện tích đáy SABCD = 24 $cm^{2}$ và có thể tích V = 84 $cm^{3}$. Chiều cao của hình hộp chữ nhật có độ dài là?

• A. h = 4 cm    

• B. h = 3,5 cm 

• C. h = 5 cm   
• D. h = 2 cm 

Câu 17: Hãy chọn câu đúng. Nếu tam giác ABC đồng dạng với tam giác MNP theo tỉ số k thì tam giác MNP đồng dạng với tam giác ABC theo tỉ số:

• A. $\frac{1}{k^{2}}$

• B. $\frac{1}{k}$

• C. $k^{2}$
• D. k

Câu 18: Với điều kiện nào của x thì biểu thức B = $\frac{2x-4}{3-x}$ nhận giá trị không âm.

• A. 2 ≤ x < 3 

• B. x ≥ 2 hoặc x < 3
• C. 2 ≤ x ≤ 3 
• D. 2 < x < 3 

Câu 19: Cho hình lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là hình chữ nhật, AB = 4cm BC = 5cm, chiều cao h = 2,5cm. Diện tích xung quanh của hình lăng trụ đứng là?

• A. Sxq = 22,5 $cm^{2}$

• B. Sxq = 45 $cm^{2}$

• C. Sxq = 30 $cm^{2}$ 
• D. Sxq = 36 $cm^{2}$

Câu 20: Nghiệm của phương trình $\frac{3x-2}{x+7}=\frac{6x+1}{2x+3}$ là?

• A. x = -1

• B. x = $\frac{-1}{56}$

• C. x = 1
• D. x = $\frac{1}{56}$

Câu 21: Một hình lăng trụ đứng có đáy là hình thoi với các đường chéo của đáy bằng 16 cm và 30 cm. Diện tích toàn phần của hình lăng trụ bằng 1840$cm^{2}$. Tính chiều cao của hình lăng trụ.

• A. 15 cm

• B. 20 cm

• C. 30 cm
• D. 25 cm

Câu 22: Bất phương trình $\frac{3x+5}{2}-1\leq \frac{x+2}{3}+x$ có nghiệm là:

• A. Vô nghiệm     
• B. x ≥ 4, 11
• C. Vô số nghiệm

• D. x ≤ −5

Câu 23: Tập nghiệm nào sau đây là tập nghiệm của bất phương trình: x ≤ 2 ?

• A. S = {x| x ≥ 2}.

• B. S = {x| x ≤ 2}.

• C. S = {x| x ≥ - 2}.
• D. S = {x| x < 2}.

Câu 24: Cho lăng trụ đứng có kích thước như hình vẽ.

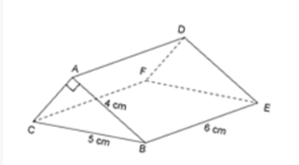
Số nào trong các số sau đây là thể tích của hình lăng trụ đứng đó?

• A. 20 $cm^{3}$

• B. 36 $cm^{3}$

• C. 26 $cm^{3}$
• D. 9 $cm^{3}$

Câu 25: Cho hình chóp tam giác đều S. ABC có tất cả các cạnh bằng 2dm. Tính độ dài đoạn thẳng MN nối trung điểm 2 cạnh đối AB và SC.

• A. MN = $\sqrt{2}$ dm

• B. MN = 2 dm
• C. MN = 4 dm
• D. MN = $\sqrt{8}$ dm

Câu 26: Cho a > b. So sánh 5 - a với 5 - b

• A. 5 - a ≥ 5 - b.
• B. 5 - a > 5 - b.
• C. 5 - a ≤ 5 - b.

• D. 5 - a < 5 - b.

Câu 27: Cho tam giác ABC. Một đường thẳng song song song với BC cắt các cạnh AB và AC theo thứ tự tại D và E. Qua E kẻ đường thẳng song song với CD, cắt AB ở F. Biết AB = 16, AF = 9, độ dài AD là:      

• A. 10 cm 
• B. 15 cm 

• C. 12 cm

• D. 14 cm

Câu 28: Bất phương trình $(x+2)^{2}$ < $x+ x^{2} - 3$ có nghiệm là:

• A. x > $\frac{-7}{3}$
• B. x > $\frac{7}{3}$

• C. x < $\frac{-7}{3}$

• D. x < $\frac{7}{3}$

Câu 29: Cho tam giác ABC. Các điểm D, E, F theo thứ tự là trung điểm của BC, CA, AB. Các điểm A′, B′, C′ theo thứ tự là trung điểm của EF, DF, DE. Chọn câu đúng?

• A. ΔA′B′C′ ∽ ΔABC theo tỉ số k = $\frac{1}{2}$      
• B. ΔEDF ∽ ΔABC theo tỉ số k = $\frac{1}{2}$

• C. ΔA′B′C′ ∽ ΔABC theo tỉ số k = $\frac{1}{4}$

• D. ΔA′B′C′ ∽ ΔEDF theo tỉ số k = $\frac{1}{2}$  

Câu 30: Với x, y bất kì, chọn khẳng định đúng?

• A. $(x+y)^{2}$ ≤ 4xy
• B. $(x+y)^{2}$ > 4xy
• C. $(x+y)^{2}$ < 4xy

• D. $(x+y)^{2}$ ≥ 4xy

Câu 31: Cho hình chóp tam giác đều S. ABC có các mặt là các tam giác đều. Gọi SH là đường cao của hình chóp, HC = $2\sqrt{3} cm$. Tính diện tích xung quanh hình chóp.

• A. $18\sqrt{3} cm^{2}$
• B. $9\sqrt{3} cm^{2}$

• C. $27\sqrt{3} cm^{2}$

• D. 27$cm^{2}$

Câu 32: Tìm x để biểu thức sau có giá trị dương A = $\frac{x+27}{5}-\frac{3x-7}{4}$

• A. x ≤ 13                      
• B. x > 13                 

• C. x < 13

• D. x ≥ 13

Câu 33: Số nguyên lớn nhất thỏa mãn bất phương trình $(x-2)^{2}-x^{2}-8x+3 \geq  0$ là:

• A. x = −2 
• B. x = 0

• C. x = −1      

• D. x ≤ −712

Câu 34: Giá trị của m để phương trình | x - m | = 2 có nghiệm là x = 1 ?

• A. m ∈ { 1 }

• B. m ∈ { - 1;3 }

• C. m ∈ { - 1;0 }
• D. m ∈ { 1;2 }

Câu 35: Tập nghiệm của phương trình $\frac{x+1}{x-1}-\frac{x-1}{x+1}=\frac{4}{x^{2}-1}$ là?

• A. S = { ± 1 }.   
• B. S = { 0;1 }.
• C. S = { 1 }.   

• D. S = { Ø }.

Câu 36: Cho phương trình (1): $\frac{1}{x}+\frac{2}{x-2}=0$ và phương trình (2): $\frac{x-1}{x^{2}-x}+\frac{2x-2}{x^{2}-3x+2}=0$. Khẳng định nào sau đây là sai.

• A. Hai phương trình có cùng điều kiện xác định.

• B. Hai phương trình có cùng số nghiệm
• C. Hai phương trình có cùng tập nghiệm
• D. Hai phương trình tương đương

Câu 37: Cho ΔABC. Tia phân giác góc trong của góc A cắt BC tại D. Cho AB = 6, AC = x, BD = 9, BC = 21. Tính kết quả đúng của độ dài cạnh x ?

• A. x = 14   
• B. x = 12

• C. x = 8   

• D. x = 6

Câu 38: Cho hình chóp tứ giác đều S. ABCD, đáy ABCD là hình vuông có cạnh 3cm, cạnh bên SB bằng 5cm. Tính diện tích xung quanh hình chóp

• A. $3\sqrt{91} cm^{2}$

• B. $6\sqrt{91} cm^{2}$
• C. $\sqrt{91} cm^{2}$
• D. 91 $cm^{2}$

Câu 39: Tính diện tích xung quanh của một hình lăng trụ đứng có đáy là hình ngũ giác đều cạnh 8 cm, biết rằng chiều cao của hình lăng trụ đứng là 5 cm.

• A. 80 $cm^{2}$
• B. 60 $cm^{2}$
• C. 120 $cm^{2}$

• D. 200 $cm^{2}$

Câu 40: Số nghiệm của phương trình $\frac{2x^{2}-x-3}{(2x-3)(x^{2}+x+1)}-\frac{2x^{2}-5x+3}{(2x-3)(x^{2}-x+1)}=\frac{6x-9}{x(2x-3)(x^{4}+x^{2}+1)}$ là:

• A. 0

• B. 1
• C. 2
• D. 3