Trắc nghiệm toán 8 hình học chương 3: Tam giác đồng dạng (P3)
Bài có đáp án. Bộ bài tập trắc nghiệm toán 8 hình học chương 3: Tam giác đồng dạng (P3). Học sinh luyện tập bằng cách chọn đáp án của mình trong từng câu hỏi. Dưới cùng của bài trắc nghiệm, có phần xem kết quả để biết bài làm của mình. Kéo xuống dưới để bắt đầu.
Câu 1: Cho tam giác ABC vuông ở A, đường cao AH. Cho BH = 9cm, HC = 16cm. Tính diện tích của tam giác ABC.
- A. 250 $cm^{2}$
- B. 300 $cm^{2}$
C. 150 $cm^{2}$
- D. 200 $cm^{2}$
Câu 2: Cho ΔABC nhọn, kẻ đường cao BD và CE, vẽ các đường cao DF và EG của ΔADE. Chọn khẳng định đúng?
- A. AD.AE = AB.AF.
B. AD.AE = AB.AG = AC.AF
- C. AD.AE = AC.GA
- D. AD.AE = AB.AF = AC.AG
Câu 3: Tính x trong trường hợp sau:

A. x = 4,5
- B. x = 3
- C. x = 2
- D. Cả 3 đáp án trên đều sai
Câu 4: Cho ΔA′B′C′ đồng dạng với ΔABC có chu vi lần lượt là 50 cm và 60 cm. Diện tích của ΔABC lớn hơn diện tích của ΔA′B′C′ là 33 $cm^{2}$. Tính diện tích tam giác ABC.
- A. 98 $cm^{2}$
- B. 216 $cm^{2}$
- C. 59 $cm^{2}$
D. 108 $cm^{2}$
Câu 5: Cho tam giác MNP vuông ở M và có đường cao MK. Khi đó
- A. ΔKNM ∽ΔMNP ∽ ΔKMP.
- B. $MK^{2} = NK.PK$
- C. Cả A, B đều sai
D. Cả A, B đều đúng
Câu 6: Cho ΔABC có BD là đường phân giác, AB = 8 cm, BC = 10 cm, AC = 6cm. Chọn phát biểu đúng?
A. DA = $\frac{8}{3}$ cm, DC = $\frac{10}{3}$ cm
- B. DA = $\frac{10}{3}$ cm, DC = $\frac{8}{3}$ cm
- C. DA = 4 cm, DC = 2 cm
- D. DA = 3,5 cm, DC = 2,5 cm
Câu 7: Tính các độ dài x, y trong hình bên:
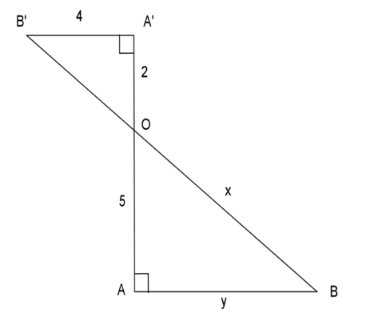
- A. x = $2\sqrt{5}$, y = 10
- B. x = $10\sqrt{5}$, y = 9
- C. x = $6\sqrt{5}$, y = 10
D. x = $5\sqrt{5}$, y = 10
Câu 8: Cho tam giác nhọn ABC có $\widehat{C} = 40^{\circ}$. Vẽ hình bình hành ABCD. Gọi AH, AK theo thứ tự là các đường cao của các tam giác ABC, ACD. Tính số đo $\widehat{AKH}$.
- A. $30^{\circ}$
B. $40^{\circ}$
- C. $45^{\circ}$
- D. $50^{\circ}$
Câu 9: Một tam giác có cạnh nhỏ nhất bằng 8, hai cạnh còn lại bằng x và y(x < y). Một tam giác khác có cạnh lớn nhất bằng 27, hai cạnh còn lại cũng bằng x và y. Tính x và y để hai tam giác đó đồng dạng.
- A. x = 5; y = 10.
- B. x = 6; y = 12
C. x = 12; y = 18
- D. x = 6; y = 18
Câu 10: Cho tam giác ABC có AB = 8cm, AC = 16cm. Điểm D thuộc cạnh AB sao cho BD = 2cm. Điểm E thuộc cạnh AC sao cho CE = 13cm. Chọn câu sai.
- A. $\widehat{ABE} = \widehat{ACD}$
B. AE.CD = AD.BC
- C. AE.CD = AD.BE
- D. AE.AC = AD.AB
Câu 11: Cho hình vẽ:
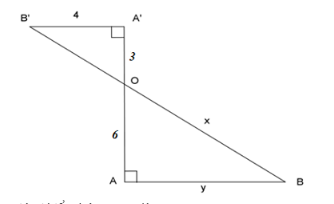
Giá trị biểu thức x − y là:
- A. 5
- B. 3
- C. 4
D. 2
Câu 12: Cho tam giác ABC, phân giác AD. Gọi E, F lần lượt là hình chiếu của B và C lên AD.
Chọn khẳng định không đúng.
- A. AE. CF = AF. BE
B. AE. DF = $ED^{2}$
- C. AE. DF = AF. DE
- D. $\frac{BE}{CF} = \frac{DE}{DF}$
Câu 13: Cho hình bình hành ABCD, điểm F trên cạnh BC. Tia AF cắt BD và DC lần lượt ở E và G. Chọn khẳng định sai.
- A. ΔBFE ∽ ΔDAE
- B. ΔDEG ∽ ΔBEA
C. ΔBFE ∽ ΔDEA
- D. ΔDGE ∽ ΔBAE
Câu 14: Cho hình bình hành ABCD có I là giao điểm của AC và BD. E là một điểm bất kì thuộc BC, qua E kẻ đường thẳng song song với AB và cắt BD, AC, AD tại G, H, F. Chọn kết luận sai?
A. ΔBGE ∽ ΔHGI
- B. ΔGHI ∽ ΔBAI
- C. ΔBGE ∽ ΔDGF
- D. ΔAHF ∽ ΔCHE
Câu 15: Cho ΔABC cân tại A, có BC = 2a, M là trung điểm BC, lấy D, E thuộc AB, AC sao cho $\widehat{DME } = \widehat{ABC}$. Tích BD.CE bằng
- A. 2a
- B. 3a
C. a
- D. 4a
Câu 16: Tìm giá trị của trên hình vẽ
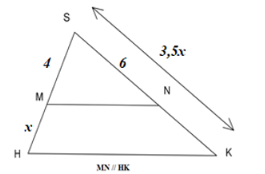
A. x = 3
- B. x = 2, 5
- C. x = 1
- D. x = 3, 5
Câu 17: Cho tam giác ABC, $\widehat{A} = 90^{\circ}$, AB = 15cm, AC = 20cm,đường cao AH (H ∈ BC). Tia phân giác của $\widehat{HAB}$ cắt HB tại D. Tia phân giác của $\widehat{HAC}$ cắt HC tại E. Tính DH?
A. 4cm
- B. 6cm
- C. 9cm
- D. 12cm
Câu 18: Cho ΔABC vuông góc tại A có BC = 5cm, AC = 3cm, EF = 3cm, DE = DF = 2,5cm. Chọn phát biểu đúng?
- A. ΔABC ∼ ΔDEF
B. $\widehat{ABC} = \widehat{EFD}$
- C. $\widehat{ACB }= \widehat{ADF}$
- D. $\widehat{ACB }= \widehat{DEF}$
Câu 19: Cho tam giác ABC, điểm M thuộc cạnh BC sao cho $\frac{MB}{MC} = \frac{1}{2}$. Đường thẳng đi qua M và song song với AC cắt AB ở D. Đường thẳng đi qua M và song song với AB cắt AC ở E. Biết chu vi tam giác ABC bằng 30cm. Chu vi của các tam giác DBM và EMC lần lượt là
- A. 10 cm; 15 cm.
- B. 12 cm; 16 cm.
- C. 20 cm; 10 cm.
D. 10 cm; 20 cm.
Câu 20: ΔDEF∽ΔABC theo tỉ số k1, ΔMNP∽ΔDEF theo tỉ số k2. Vậy ΔABC∽ΔMNP theo tỉ số nào?
A. $\frac{1}{k1.k2}$
- B. $\frac{k2}{k1}$
- C. k1.k2
- D. $\frac{k1}{k2}$

Bình luận