A. HOẠT ĐỘNG KHỞI ĐỘNG

Thực hiện các hoạt động sau

a) Cho tam giác ABC. Có thể lấy điểm D trên BC sao cho $\frac{BD}{AB}$ = $\frac{DC}{AC}$ được không? Dự đoán vị trí điểm D.

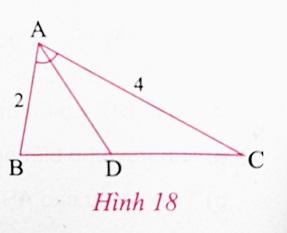
b) Vẽ tam giác ABC thỏa mãn AB = 2cm, AC = 4cm và $\widehat{A}$ = $80^{\circ}$ (h.8).

- Dựng đường phân giác AD của góc A ( bằng thước thẳng và compa).

- Đo độ dài các đoạn thẳng BD và DC rồi so sánh các tỉ số $\frac{AB}{AC}$ = $\frac{DB}{DC}$.

Trả lời:

a) Có thể lấy điểm D trên BC sao cho $\frac{BD}{AB}$ = $\frac{DC}{AC}$. 

Dự đoán: điểm D là giao điểm giữa đường phân giác góc A của tam giác ABC với cạnh BC.

b) Ta đo được BD = 1,2cm, DC = 2,4cm

$\Rightarrow $ $\frac{DB}{DC}$ = $\frac{1,2}{2,4}$ = $\frac{1}{2}$

$\frac{AB}{AC}$ = $\frac{2}{4}$ = $\frac{1}{2}$

Vậy $\frac{DB}{DC}$ = $\frac{AB}{AC}$.

B. HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC

b. Điền vào chỗ trống (...) để hoàn thiện giả thiết - kết luận và chứng minh định lí trên.

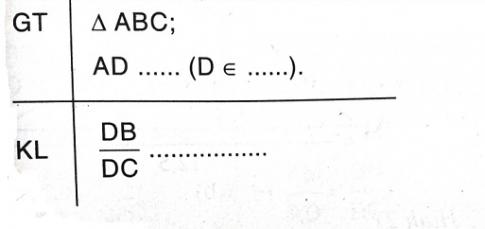
Chứng minh

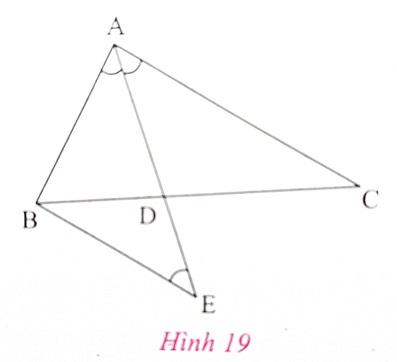
Qua đỉnh B vẽ đường thẳng song song với AC cắt AD tại E (h.19).

Ta có: $\widehat{BAE}$ =      (...)

Vì BE // AC, nên $\widehat{BAE}$ = .......(so le trong).

Suy ra.................................Do đó $\Delta $ABE cân tạ B, suy ra BE = BA.

Áp dụng hệ quả của định lí Ta -lét đối với $\Delta $DAC, ta có: $\frac{DB}{DC}$ = $\frac{....}{....}$.

Từ (1) và (2) suy ra $\frac{DB}{DC}$ = $\frac{AB}{AC}$.

Trả lời:

Chứng minh

Qua đỉnh B vẽ đường thẳng song song với AC cắt AD tại E (h.19).

Ta có: $\widehat{BAE}$ = $\widehat{EAC}$ 

Vì BE // AC, nên $\widehat{BEA}$ = $\widehat{EAC}$ (so le trong).

Suy ra $\widehat{BEA}$ = $\widehat{BAE}$. Do đó $\Delta $ABE cân tạ B, suy ra BE = BA.

Áp dụng hệ quả của định lí Ta -lét đối với $\Delta $DAC, ta có: $\frac{DB}{DC}$ = $\frac{BE}{AC}$.

Từ (1) và (2) suy ra $\frac{DB}{DC}$ = $\frac{AB}{AC}$.

c) Cho hình 20. Tính x, y, z.

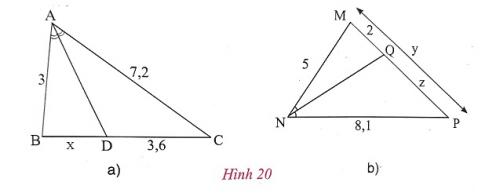
- Hướng dẫn (h.20): Xét $\Delta $ABC, ta có AD là phân giác của $\widehat{BAC}$, suy ra $\frac{BD}{DC}$ = $\frac{AB}{AC}$.

Hay $\frac{x}{3,6}$ = $\frac{3}{7,2}$, suy ra x = $\frac{3,6.3}{7,2}$ = 1,5.

Trả lời:

* Xét $\Delta $MNP, ta có NQ là phân giác của $\widehat{MNP}$, suy ra $\frac{QM}{QP}$ = $\frac{NM}{NP}$.

Hay $\frac{2}{z}$ = $\frac{5}{8,1}$, suy ra z = $\frac{2.8.1}{5}$ = 3.24

Suy ra: y = z + 2 = 5,24.