A. HOẠT ĐỘNG KHỞI ĐỘNG

Thực hiện các hoạt động sau

- Tỉ số của hai số a và b (b $\neq $ 0) là gì? Hãy viết tỉ số của hai số a và b.

- Đọc:

+ Tỉ số của hai đoạn thẳng AB = 3cm và CD = 4cm là AB : CD = 3 : 4 (h.1).

+ Tỉ số của hai đoạn thẳng MN = 3cm và PQ = 2dm là MN : PQ = 3 : 20 (2dm = 20cm).

- Vậy theo em tỉ số của hai đoạn thẳng là gì?

Trả lời:

- Tỉ số của hai số a và b (b $\neq $ 0) là thương của phép chia số a cho số b (b $\neq $ 0).

  Tỉ số của hai số a và b được viết là $\frac{a}{b}$ hoặc a : b

- Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng đơn vị đo.

B. HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC

1. Thực hiện các hoạt động sau để tìm tỉ số của hai đoạn thẳng

b) - Tính tỉ số của EF = 36cm và GH = 12dm.

    - Tính tỉ số của PQ = 1,3m và MN = 26cm.

Trả lời:

- Tỉ số: EF : GH = 36 : 120 = 3 : 10

- Tỉ số: PQ : MN = 130 : 26 = 5 :1

2. a) Thực hiện các hoạt động sau

Cho bốn đoạn thẳng AB = 2cm, CD = 4cm, A'B' = 5cm, C'D' = 10cm.

So sánh các tỉ số AB : CD và A'B' = C'D".

Trả lời:

Tỉ số $\frac{AB}{CD}$ = AB : CD = 2 : 4 = 1 : 2

Tỉ số $\frac{A'B'}{C'D'}$ = A'B' = C'D" = 5 : 10 = 1 :2

Vậy $\frac{AB}{CD}$  = $\frac{A'B'}{C'D'}$.

c) Cho hình 2. Vẽ tam giác ABC trên giấy vở kẻ ngang. Vẽ đường thẳng a song song với BC, cắt hai cạnh AB, AC theo thứ tự tại B' và C'.

Đường thẳng a định ra trên cạnh AB ba đoạn thẳng AB', B'B, AB và định ra trên cạnh AC ba đoạn thẳng tương ứng là AC', C'C và AC.

So sánh các tỉ số: $\frac{AB'}{AB}$ và $\frac{AC'}{AC}$; $\frac{AB'}{BB'}$  và $\frac{AC'}{CC'}$ ; $\frac{BB'}{AB}$ và $\frac{CC'}{AC}$.

Mẫu: Vì AB' có số đo là 5 đơn vị độ dài, AB có số đo bằng 8 đơn vị độ dài nên $\frac{AB'}{AB}$ = $\frac{5}{8}$.

Vì AC' có số đo là 5 đơn vị độ dài, AC có số đo bằng 8 đơn vị độ dài nên $\frac{AC'}{AC}$ = $\frac{5}{8}$.

Vậy $\frac{AB'}{AB}$ = $\frac{AC'}{AC}$.

* Hãy so sánh các cặp tỉ số còn lại.

Trả lời:

* So sánh: $\frac{AB'}{BB'}$  và $\frac{AC'}{CC'}$

Vì AB' có số đo là 5 đơn vị độ dài, BB' có số đo bằng 3 đơn vị độ dài nên $\frac{AB'}{BB'}$ = $\frac{5}{3}$.

Vì AC' có số đo là 5 đơn vị độ dài, CC' có số đo bằng 3 đơn vị độ dài nên $\frac{AC'}{CC'}$ = $\frac{5}{3}$.

Vậy $\frac{AB'}{BB'}$ = $\frac{AC'}{CC'}$.

* So sánh: $\frac{BB'}{AB}$ và $\frac{CC'}{AC}$

Vì BB' có số đo là 3 đơn vị độ dài, AB có số đo bằng 8 đơn vị độ dài nên $\frac{BB'}{AB}$ = $\frac{3}{8}$.

Vì CC' có số đo là 3 đơn vị độ dài, AC có số đo bằng 8 đơn vị độ dài nên $\frac{CC'}{AC}$ = $\frac{3}{8}$.

Vậy $\frac{BB'}{AB}$ = $\frac{CC'}{AC}$.

3. Định lí Ta-lét trong tam giác

b) Viết giả thiết, kết luận và vẽ hình của định lý trên.

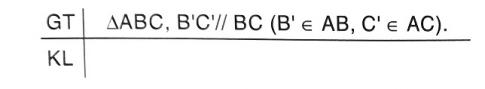
Trả lời:

c) Ví dụ: Tính x trong hình 3, biết AM = 4cm, ME  2cm, AN = 5,5cm và MN song song với EF.

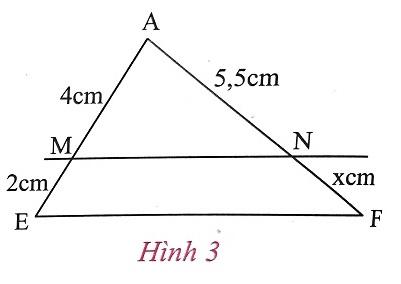
Giải: Vì MN // EF, theo định lí Ta-lét ta có:

................................................................

Suy ra x =.............= 2,75 (cm).

Trả lời:

Vì MN // EF, theo định lí Ta-lét ta có:

$\frac{AM}{AE}$ = $\frac{AN}{AF}$ $\Leftrightarrow $ $\frac{4}{6}$ = $\frac{5,5}{5,5 + x}$

Suy ra x = $\frac{11}{4}$ = 2,75 (cm).

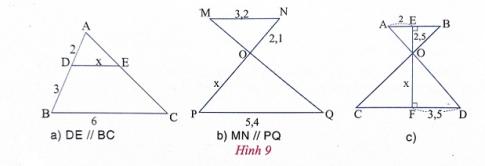
d) Tính x,y trong hình 4

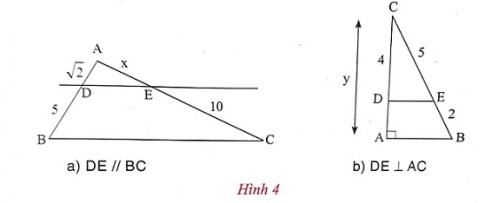
Trả lời:

* Vì DE // BC, theo định lí Ta-lét ta có:

$\frac{AD}{AB}$ = $\frac{AE}{AC}$ $\Leftrightarrow $ $\frac{\sqrt{2}}{\sqrt{2} + 5}$ = $\frac{x}{x + 10}$

Suy ra x = 2$\sqrt{2}$.

* Vì DE // AB, theo định lí Ta-lét ta có:

$\frac{CD}{CA}$ = $\frac{CE}{CB}$ $\Leftrightarrow $ $\frac{4}{y}$ = $\frac{5}{5 + 2}$

Suy ra y = 5,6.

4. Định lí Ta-lét đảo

a) Cho tam giác AEF có AE = 6cm; AF = 9cm, Lấy trên AE điểm M, trên AF điểm N sao cho ME = 2cm; NF = 3cm (h.5a).

* So sánh các tỉ số $\frac{ME}{AM}$ và $\frac{NF}{AN}$.

* Vẽ đường thẳng a đi qua M và song song với EF, đường thẳng a cắt AF tại N'.

* Tính độ dài đoạn thẳng N'F'.

* Hãy nhận xét vị trí của hai điểm N và N'; hai đoạn thẳng MN và MN'.

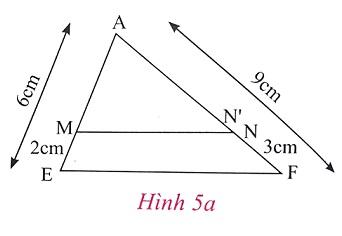
Trả lời:

* Ta có:

$\frac{ME}{AM}$ = $\frac{2}{4}$ = $\frac{1}{2}$

$\frac{NF}{AN}$ = $\frac{3}{6}$ = $\frac{1}{2}$.

Vậy $\frac{ME}{AM}$ = $\frac{NF}{AN}$.

* Vì MN' // EF, theo định lí Ta-lét ta có:

$\frac{AM}{AE}$ = $\frac{AN'}{AF}$ $\Leftrightarrow $ $\frac{4}{6}$ = $\frac{AN'}{9}$

Suy ra AN' = 6cm suy ra N'F = 3cm.

* Ta có: N thuộc AF và NF =3cm

             N' thuộc AF và N'F = 3cm

Suy ra N $\equiv $ N' và MN = MN'.

5. Thực hiện các hoạt động sau để tìm hiểu hệ quả của định lí Ta-lét

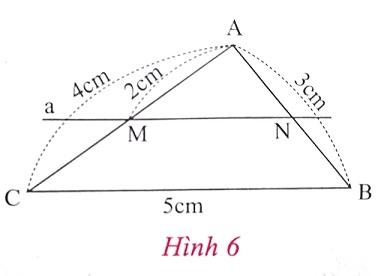
a) Cho tam giác ABC có AB = 3cm, AC = 4cm, BC = 5cm. Kẻ một đường thẳng a song song với BC cắt AB và AC lần lượt tại M và N sao cho AM = 2cm (h.6).

* Tam giác ABC là tam giác gì? Chứng minh.

* Tính AN, MM.

* Tính tỉ số $\frac{AM}{AB}$, $\frac{AN}{AC}$, $\frac{MN}{BC}$.

* Có nhận xét gì về tỉ số các cạnh tương ứng của tam giác ABC và tam giác AMN?

Trả lời:

* Ta có: $AC^{2}$ + $AB^{2}$ = $3^{2}$ + $4^{2}$ = 25 = $5^{2}$ = $BC^{2}$

Suy ta tam giác ABC là tam giác vuông tại A.

* Vì MN // BC, theo định lí Ta-lét ta có:

$\frac{AM}{AC}$ = $\frac{AN}{AB}$ $\Leftrightarrow $ $\frac{2}{4}$ = $\frac{AN}{3}$ $\Leftrightarrow $ AN = $\frac{3}{2}$

$\frac{MN}{BC}$ = $\frac{AM}{AC}$ $\Leftrightarrow $ $\frac{MN}{5}$ = $\frac{2}{4}$ $\Leftrightarrow $ MN = $\frac{5}{2}$.

* $\frac{AM}{AB}$ = $\frac{2}{3}$

  $\frac{AN}{AC}$ = $\frac{\frac{3}{2}}{4}$ = $\frac{3}{8}$

  $\frac{MN}{BC}$ = $\frac{\frac{5}{2}}{5}$ = $\frac{1}{2}$.

* Ta có:

$\frac{AM}{AC}$ = $\frac{2}{4}$ =  $\frac{1}{2}$

$\frac{AN}{AB}$ = $\frac{\frac{3}{2}}{3}$ = $\frac{1}{2}$

$\frac{MN}{BC}$ = $\frac{\frac{5}{2}}{5}$ = $\frac{1}{2}$

Vậy $\frac{AM}{AC}$ = $\frac{AN}{AB}$ = $\frac{MN}{BC}$ hay tỉ số các cạnh tương ứng của tam giác ABC và tam giác AMN bằng nhau.

c) Chứng minh hệ quả trên

* Viết giả thiết và kết luận của định lí trên.

* Gợi ý: Qua C' kẻ đường thẳng song song với AB và cắt BC tại D (h.7).

Chứng tỏ tứ giác B'C'DB là hình bình hành. Suy ra B'C' = BD.

Áp dụng định lí Ta-lét ta có $\frac{AB'}{AB}$ = $\frac{AC'}{AC}$ = $\frac{BD}{BC}$ = $\frac{B'C'}{BC}$.

Trả lời:

* Giả thiết, kết luận:

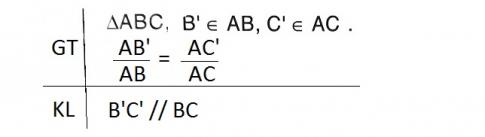
* Qua C' kẻ đường thẳng song song với AB và cắt BC tại D

Ta có: B'C' // BD, B'B // C'D $\Rightarrow $ B'C'DB là hình bình hành

$\Rightarrow $ B'C' = BD

Vì B'C' // BC theo định lí Ta-lét ta có:

$\frac{AB'}{AB}$ = $\frac{AC'}{AC}$ = $\frac{B'C'}{BC}$ = $\frac{BD}{BC}$ ( do B'C' = BD)