Giải toán VNEN 8 bài 7: Trường hợp đồng dạng thứ ba
Giải bài 7: Trường hợp đồng dạng thứ ba - Sách VNEN toán 8 tập 2 trang 72. Phần dưới sẽ hướng dẫn trả lời và giải đáp các câu hỏi trong bài học. Cách làm chi tiết, dễ hiểu, Hi vọng các em học sinh nắm tốt kiến thức bài học.
A.B. HOẠT ĐỘNG KHỞI ĐỘNG và HÌNH THÀNH KIẾN THỨC
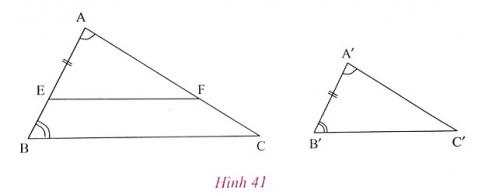
1. a) Cho $\Delta $ ABC và $\Delta $ A'B'C' như hình 41. Chứng tỏ $\Delta $ ABC $\sim $ $\Delta $ A'B'C'
Điền vào chỗ trống (...) để hoàn thiện lời giải
Lấy E trên AB sao cho AE = A'B'. Từ E kẻ đường thẳng song song với BC cắt Ac tại F.
Suy ra: $\Delta $ AEF $\sim $ $\Delta $...... và $\widehat{AEF}$ = $\widehat{ABC}$ (hai góc đồng vị).
Do $\widehat{A'B'C'}$ =..........( giả thiết) nên $\widehat{AEF}$ = $\widehat{A'B'C'}$.
Vì vậy $\Delta $ AEF = $\Delta $ A'B'C' ( $\widehat{A}$ = $\widehat{A'}$; AE = A'B'; $\widehat{AEF}$ = $\widehat{A'B'C'}$).
Nên $\Delta $ AEF $\sim $ $\Delta $.......
Từ (1) và (2) suy ra $\Delta $ ABC $\sim $ $\Delta $.......
Trả lời:
Lấy E trên AB sao cho AE = A'B'. Từ E kẻ đường thẳng song song với BC cắt Ac tại F.
Suy ra: $\Delta $ AEF $\sim $ $\Delta $ ABC và $\widehat{AEF}$ = $\widehat{ABC}$ (hai góc đồng vị).
Do $\widehat{A'B'C'}$ =$\widehat{ABC}$ ( giả thiết) nên $\widehat{AEF}$ = $\widehat{A'B'C'}$.
Vì vậy $\Delta $ AEF = $\Delta $ A'B'C' ( $\widehat{A}$ = $\widehat{A'}$; AE = A'B'; $\widehat{AEF}$ = $\widehat{A'B'C'}$).
Nên $\Delta $ AEF $\sim $ $\Delta $ A'B'C'
Từ (1) và (2) suy ra $\Delta $ ABC $\sim $ $\Delta $ A'B'C'.
c) Trong các tam giác dưới đây (h.42), những cặp tam giác nào đồng dạng với nhau? Hãy giải thích.
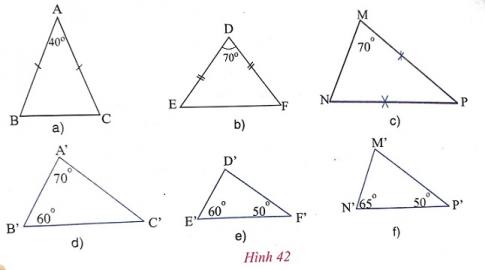
Trả lời:
Trong hình 42d và 42e.
$\Delta $ A'B'C' có $\widehat{A'}$ = $70^{\circ}$ ; $\widehat{B'}$ = $60^{\circ}$ $\Rightarrow $ $\widehat{C'}$ = $50^{\circ}$
$\Delta $ D'E'F' có $\widehat{E'}$ = $60^{\circ}$; $\widehat{F'}$ = $50^{\circ}$ $\Rightarrow $ $\widehat{D'}$ = $70^{\circ}$
Vì $\Delta $ A'B'C' và $\Delta $ D'E'F' có $\widehat{A'}$ = $\widehat{D'}$ = $70^{\circ}$; $\widehat{B'}$ =$\widehat{E'}$ = $60^{\circ}$ nên $\Delta $ A'B'C' $\sim $ $\Delta $ D'E'F.
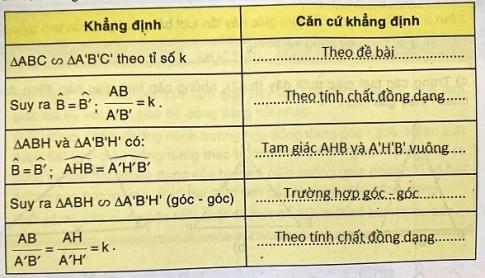
2.a) Cho ABC và A'B'C' đồng dạng có đường cao tương ứng là AH và A'H' như hình 43. Gọi tỉ số đồng dạng của hai tam giác là k. Chứng minh: $\frac{AH}{A'H'}$ = k.

Điền vào bảng sau:

Trả lời:




Bình luận