Slide bài giảng Toán 9 Chân trời bài tập cuối chương 9

Tóm lược nội dung

BÀI TẬP CUỐI CHƯƠNG 9

1. CÂU HỎI TRẮC NGHIỆM

Giải rút gọn câu 1 trang 81 sgk toán 9 tập 2 ctst

Cho tam giác đều ABC có đường cao AH = 9 cm. Bán kính r của đường tròn nội tiếp tam giác có độ dài là

A. 6 cm. B. 3 cm.  C. 4,5 cm. D. 332 cm.

Giải rút gọn:

Chọn D (r = a36=936=332 (cm))

Giải rút gọn câu 2 trang 81 sgk toán 9 tập 2 ctst

Cho tam giác ABC có AB = AC = 4 cm. Bán kính R của đường tròn ngoại tiếp tam giác có độ dài là

A. 22 cm. B. 2 cm.  C. 42 cm. D. 82 cm.

Giải rút gọn:

Chọn A ; R = BC2=AB2 + AC22=22 (cm).

Giải rút gọn câu 3 trang 81 sgk toán 9 tập 2 ctst

Tứ giác ở hình nào dưới đây là tứ giác nội tiếp đường tròn (O)?

A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4.

Giải rút gọn:

Chọn C

Giải rút gọn câu 4 trang 81 sgk toán 9 tập 2 ctst

Trong các phát biểu sau, phát biểu nào đúng?

A. Mọi tứ giác luôn nội tiếp đường tròn.

B. Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng 90^o.

C. Tổng số đo hai góc đối của một tứ giác nội tiếp luôn bằng 180^o.

D. Tất cả các hình thang đều là tứ giác nội tiếp.

Giải rút gọn:

Chọn C 

Giải rút gọn câu 5 trang 81 sgk toán 9 tập 2 ctst

Cho tứ giác MNPQ nội tiếp đường tròn (O; R) và M = 60^o. Số đo góc của P là

A. 30^o. B. 120^o. C. 180^o. D. 90^o.

Giải rút gọn:

Chọn B (M+P=180oP=180o-M=120o )

Giải rút gọn câu 6 trang 81 sgk toán 9 tập 2 ctst

Cho tứ giác ABCD nội tiếp đường tròn (O). Biết DAO = 50^o, OCD = 30^o (Hình 5). Số đo của ABC là

A. 80^o. B. 90^o.

C. 100^o. D. 110^o.

Giải rút gọn:

Chọn C vì:

OA = OD = R  Tam giác AOD cân tại O nên DAO=ADO=50o.

OC = OD = R  Tam giác COD cân tại O nên DCO=CDO=30o.

Tứ giác ABCD nội tiếp ADC+ABC=180o.

ABC=180o-ADC=180o-ADO-CDO=180o-30o-50o=100o.

Giải rút gọn câu 7 trang 81 sgk toán 9 tập 2 ctst

Cho tứ giác ABCD nội tiếp có ACD = 60^o. Khẳng định nào sau đây luôn đúng?

A. ADC = 60^o. B. ADC = 120^o. 

C. ABD = 60^o. D. ABD = 120^o. 

Giải rút gọn:

Chọn D vì  ACD có góc đối diện là ABD nên ACD+ABD=180o.

ABD=180o-ACD=180o-60o=120o.

Giải rút gọn câu 8 trang 82 sgk toán 9 tập 2 ctst

Cho lục giác đều ABCDEF nội tiếp đường tròn bán kính R. Độ dài cạnh AB bằng

A. R. B. R3. C. R32. D. R2.

Giải rút gọn:

Chọn A 

Giải rút gọn câu 9 trang 82 sgk toán 9 tập 2 ctst

Cho tam giác đều ABC có O là tâm đường tròn ngoại tiếp. Phép quay nào với O là tâm biến tam giác ABC thành chính nó?

A. 90^o. B. 100^o. C. 110^o. D. 120^o.

Giải rút gọn:

Chọn D 

2. BÀI TẬP TỰ LUẬN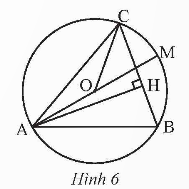

Giải rút gọn bài 10 trang 82 sgk toán 9 tập 2 ctst

Cho tam giác nhọn ABC có đường cao AH (H  BC) và nội tiếp đường tròn tâm O có đường kính AM (hình 6). Chứng minh OAC=BAH.

Giải rút gọn:

OA = OC = R nên ∆ OAC cân tại O OAC=OCA.

Vì ACM là góc nội tiếp chắn cung AM, AM là đường kính đường tròn (O).

ACM=90o hay OCA+OCM=90oOAC=OCA=90o-OCM

=90o-OMC (do OC = OM = R nên tam giác OMC cân tại O OCM=OMC).

=90o-B (do OMC  và B cùng là góc nội tiếp chắn cung AC nhỏ)

= BAH (tổng ba góc trong của tam giác).

Giải rút gọn bài 11 trang 82 sgk toán 9 tập 2 ctst

Cho tam giác ABC vuông tại A (AB < AC) có AH là đường cao. Lần lượt vẽ đường tròn (O) đường kính BH và đường tròn (O’) đường kính HC.

a) Xét vị trí tương đối của hai đường tròn (O) và (O’).

b) Đường tròn (O) cắt AB tại E, đường tròn (O’) cắt AC tại F. Chứng minh rằng tứ giác AEHF là hình chữ nhật.

c) Chứng minh rằng EF là tiếp tuyến đường tròn (O) và đồng thời là tiếp tuyến đường tròn (O’).

d) Đường trung tuyến AM của tam giác ABC cắt EF tại N. Cho biết AB = 6 cm, AC = 8 cm. Tính diện tích tam giác ANF.

Giải rút gọn:

a) Ta có OO’ = OH + O’H = R + R’ và O; H; H’ thẳng hàng.

Hai đường tròn tiếp xúc nhau.

b) Xét đường tròn (O) có BH là đường kính

BEH là góc nội tiếp chắn cung BH BEH=90o hay AB  EH tại E.

Xét đường tròn (O’) có HC là đường kính

HFC là góc nội tiếp chắn cung HC HFC=90o hay AC  HF tại F.

Xét tứ giác AEHF có: 

HEA=90o (chứng minh trên);

EAF=90o (giả thiết);

AFH=90o (chứng minh trên).

Tứ giác AEHF là hình chữ nhật.

c) Vì OE = OH = R nên ∆ OEH cân tại O OEH=OHE.

Ta có BHE=90o-B; BAH=90o-B BHE=BAH.

Mà OEH=BHE (chứng minh trên); BHA=AEF (tính chất hình chữ nhật).

OEH=AEF hay OEH+HEF=AEF+HEFOEF=AEH=90o.

EF  OE tại E; E  (O)

EF là đường trung tuyến đường tròn (O) (1).

Vì O’F = O’H = R’ ⇒∆ O’HF cân tại O’O'HF=O'HF

Mà AHF=EFH (tính chất hình chữ nhật)

O'HF+AHF=O'HF+EFH hay O'FE+AHC=90o.

EF  O’F tại F; F  (O’)

EF là đường trung tuyến đường tròn (O’) (2).

Từ (1) và (2)  điều phải chứng minh.

d) Ta có: AEF=BAH=90o-B (tổng ba góc trong của tam giác).

C=90o-B (tổng ba góc trong của tam giác).

AEF=BAH=C mà C=NAF (do AM = MC = BM = 12 BC nên ∆ AMC cân tai M).

AEF=NAF.

∆ ANF đồng dạng  ∆ EAF (g – g)

SANFSEAF=AF2EF2=AF2AH2 (EF = AH do AEHF là hình chữ nhật).

∆ AEF đồng dạng  ∆ ABC (g – g)

SAEFSABC=EF2BC2=AH2BC2 (EF = AH do AEHF là hình chữ nhật).

Ta có EF2=AH2=AB2. AC2AB2 + AC2=82. 6282 + 62=23,04 (hệ thức lượng trong tam giác vuông).

AH = 4,8 cm.

BC² = AB² + AC² = 6² + 8² =100 (Định lý Pytagore).

BC = 10 cm.

AH² = AF.AC (hệ thức lượng trong tam giác vuông).

AF=AH2AC=4,828 = 2,88 cm.

Vậy SAEFSABC=AH2BC2=4,82102=144625SAEF=144625.SABC=144625.12.AB.AC = 5,53 cm².

SANFSEAF=AF2AH2=2,8824,82=925SANF=925.SEAF = 1,99cm².

Giải rút gọn bài 12 trang 82 sgk toán 9 tập 2 ctst

Mái nhà trong Hình 7 được đỡ bởi khung đa giác đều. Gọi tên đa giác đó. Tìm phép quay biến đa giác đó thành chính nó.

Giải rút gọn:

Đa giác có tên gọi là thập nhị giác đều. Các phép quay biến nó thành chính nó là các phép quay: 30^o, 60^o, 90^o, 120^o, 150^o, 180^o, 210^o, 240^o, 270^o, 300^o, 330^o hoặc 360^o theo chiều kim đồng hồ hay ngược chiều kim đồng hồ.