Slide bài giảng Toán 9 Chân trời bài tập cuối chương 5

Tóm lược nội dung

ÔN TẬP CUỐI CHƯƠNG 5

1. CÂU HỎI TRẮC NGHIỆM

Câu 1: C

Câu 2: A

Câu 3: D

Câu 4: A

Câu 5: C

Câu 6: C

Câu 7: A

Câu 8: D

Câu 9: C

Câu 10: D

2. BÀI TẬP TỰ LUẬN

Giải rút gọn bài 11 trang 104 sgk toán 9 tập 1 ctst

Quan sát Hình 4. Biệt DOA = 120°, OA OC, OBI OD.

a) Đọc tên các góc ở tâm có trong hình.

b) Tính số đo của mỗi góc ở tâm tìm được ở câu a.

c) Tìm các cặp cung bằng nhau và có số đo nhỏ hơn 180°.

d) So sánh hai cung nhỏ AB và CD.

Lời giải rút gọn:

a) Các góc ở tâm: DOC, DOB, DOA, COB, COA, BOA

b) DOC = 120^o – 90^o = 30^o

DOB = 90^o

DOA = 120^o

COB = 120^o – 30^o – 30^o = 60^o

COA = 90^o

BOA = 120^o – 90^o = 30^o

c) Các cặp cung bằng nhau:

DB = CA

CD = AB

d) AB = CD 

Giải rút gọn bài 12 trang 104 sgk toán 9 tập 1 ctst

Cho tam giác ABC có ba đỉnh nằm trên đường tròn (O) và AH là đường cao. Đường thẳng AO cắt đường tròn (O) tại điểm thứ hai D. Chứng minh rằng:

a) AC vuông góc với DC;

b) ABC = ADC;

c) AB. AC = AH. AD.

Lời giải rút gọn:

a) Vì AD là đường kính của đường tròn (đường thẳng đi qua tâm và cắt đường tròn), nên góc ADC là góc nội tiếp chắn cung AC. Do đó, ADC là tam giác nội tiếp.

=> Tam giác ADC vuông tại C

=> AC vuông góc với DC

b) Ta có ADC là góc nội tiếp chắn cung AC

ABC là góc nội tiếp chắn cung AC

=> ABC = ADC

c) Xét tam giác ABH và tam giác ADC:

ABH = ADC

AHB = ACD = 90^o

=> Tam giác ABH đồng dạng tam giác ADC

=> AB / AH = AD / AC

ó AB. AC = AD. AH

Giải rút gọn bài 13 trang 105 sgk toán 9 tập 1 ctst

Hãy hoàn thành bảng số liệu sau vào vở

Lời giải rút gọn:

Giải rút gọn bài 14 trang 105 sgk toán 9 tập 1 ctst

Trên đường thẳng xy, lấy lần lượt ba điểm A, B, C sao cho AB > BC. Vẽ đường tròn (O) đường kính AB và đường tròn (O') đường kính BC.

a) Chứng minh rằng hai đường tròn (O) và (O') tiếp xúc ngoài tại B.

b) Gọi H là trung điểm của AC. Vẽ dây DE của (O) vuông góc với AC tại H. Chứng minh tứ giác ADCE là hình thoi.

c) DC cắt đường tròn (O') tại F. Chứng minh rằng ba điểm F, B, E thẳng hàng.

d) Chứng minh rằng HF là tiếp tuyến của đường tròn (O').

Lời giải rút gọn:

a) Xét tam giác ABC, ta có AB > BC. Vì O là trung điểm của AB và O' là trung điểm của BC, nên ta có OB = O'B.

Do đó, OB là phân giác của góc ABC và O'B là phân giác của góc BCA. Vì AB > BC, nên OB sẽ cắt O'B ngoài tam giác ABC tại một điểm B nằm giữa O và O).

Vậy, hai đường tròn (O) và (O') tiếp xúc ngoài tại B.

b) Gọi H là trung điểm của AC. Vì H là trung điểm của AC, nên AH = HC.

Xét tam giác AHE, với O là trung điểm của AE, H là trung điểm của AC, và OE là đoạn thẳng nối hai trung điểm, nên ta có OE song song AC và OE = AC/2

Vậy, DE là dây chứa giữa của đường tròn (O), vuông góc với AC tại H.

Do đó, tứ giác ADCE là hình thoi với AC là đường chéo và DE là dây chứa giữa của nó.

c) Gọi F là điểm cắt của DC và đường tròn (O'). 

Có OB = O'B.

Ta cũng đã biết rằng DE là dây chứa giữa của đường tròn (O) vuông góc với AC tại H, do đó OB là đoạn thẳng nối hai điểm tiếp xúc của DE với đường tròn (O).

Vậy, ba điểm F, B, E thẳng hàng, với B nằm giữa F và E.

d) Gọi G là giao điểm của HF và O'. 

Vì H là trung điểm của AC, nên HF là dây chứa giữa của đường tròn (O), do đó góc giữa HF và DC bằng góc mở rộng HDC trên đường tròn (O).

AB và CD là hai đường kính của đường tròn (O), nên góc HDC là góc vuông.

Như vậy, góc giữa HF và DC là góc vuông HDC.

Tương tự, ta cũng có thể chứng minh rằng góc giữa GF và DC cũng là góc vuông GDC.

Nhưng hai góc này là góc giữa hai tiếp tuyến và dây của cùng một đường tròn, nên chúng bằng nhau.

Do đó, HF cũng là tiếp tuyến của đường tròn (O') tại điểm G.

Giải rút gọn bài 15 trang 105 sgk toán 9 tập 1 ctst

Hải đăng Kê Gà toạ lạc tại xã Tân Thành, huyện Hàm Thuận Nam, tỉnh Bình Thuận. Biết ngọn hải đăng cao 65 m so với mặt nước biển. Với khoảng cách bao nhiêu kilômét thì người quan sát trên tàu bắt đầu trông thấy ngọn của hải đăng này? Cho biết mắt người quan sát ở độ cao 5 m so với mặt nước biển và bán kính Trái Đất gần bằng 6400 km.

Lời giải rút gọn:

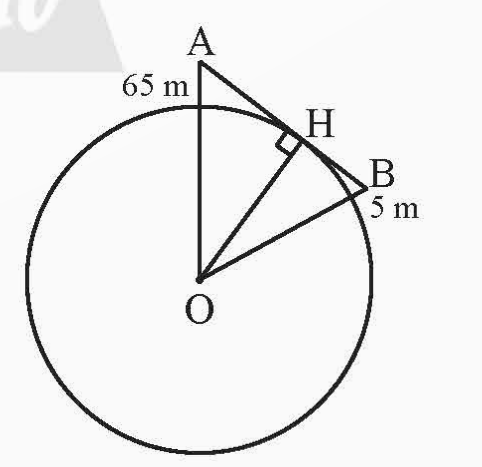
Đổi 65 m = 0,065 km; 5 m = 0,005 km

Ta có OA = 6400 + 0,065 = 6400,065 km

OH = 6400 km

Xét tam giác OHA vuông tại H

=>

Ta có OB = 6400 + 0,005 = 6400,005 km

Xét tam giác OHB vuông tại H

=>

Suy ra AB = 28,84 + 8 = 36,84 km

Vậy với khoảng cách 36,84 km thì người quan sát trên tàu bắt đầu trông thấy ngọn của hải đăng