Slide bài giảng Toán 9 Chân trời bài tập cuối chương 4

Tóm lược nội dung

BÀI TẬP CUỐI CHƯƠNG 4

1. CÂU HỎI TRẮC NGHIỆM

Câu 1: C

Câu 2: C

Câu 3: B

Câu 4: A

Câu 5: D

Câu 6: B

Câu 7: A

Câu 8: D

2. CÂU HỎI TỰ LUẬN

Giải rút gọn bài tập 9 trang 73 sgk toán 9 tập 1 ctst

Tìm số đo góc biết rằng:

a) sin

b) cos

c) tan

d) cot

Lời giải rút gọn:

a) sin =>

b) cos

c) tan

d) cot

Giải rút gọn bài tập 10 trang 73 sgk toán 9 tập 1 ctst

Cho tam giác ABC vuông tại A có AB = 18 cm, AC = 24 cm. Tính các tỉ số lượng giác của góc B, từ đó suy ra các tỉ số lượng giác của góc C

Lời giải rút gọn:

BC =

=> Các tỉ số lượng giác của góc B: sin B = AC / BC = 24 / 30 = 4 /5

cos B  = AB / BC = 18 / 30 = 3 /5 

tan B = AC / AB = 4 / 3

cot B = AB / AC = 3 / 4

Các tỉ số lượng giác của góc C: sin C = cos B  = 3 / 5

cos C = sin B  = 4 / 5

tan C = cot B = 3 / 4

cot C = tan B  = 4 / 3

Giải rút gọn bài tập 11 trang 73 sgk toán 9 tập 1 ctst

Cho tam giác ABC vuông tại A. Chứng minh rằng AC / AB = sin B / sin C

Lời giải rút gọn:

Ta có sin B  = AC / BC

sin C = AB / BC

=> sin B / sin C =  

Giải rút gọn bài tập 12 trang 73 sgk toán 9 tập 1 ctst

Cho góc nhọn Tính cos , tan và cot

Lời giải rút gọn:

sin = 0,8 =>

=> cos

tan

cot  

Giải rút gọn bài tập 13 trang 73 sgk toán 9 tập 1 ctst

Tính giá trị của biểu thức:

a) A = 4 – sin²45^o + 2cos²60^o – 3cot³45^o

b) B = tan 45^o . cos 30^o . cot 30^o

c) C = sin 15^o + sin 75^o – cos 15^o – cos 75^o + sin 30^o

Lời giải rút gọn:

a) A = 4 – sin²45^o + 2cos²60^o – 3cot³45^o

A = 4 – 0,5 + 0,25 – 3 = 0,75

b) B = tan 45^o . cos 30^o . cot 30^o

= 1 . .

c) C = sin 15^o + sin 75^o – cos 15^o – cos 75^o + sin 30^o

= (sin 15^o – cos 75^o) + (sin 75^o – cos 15^o) + sin 30^o

= ½

Giải rút gọn bài 14 trang 73 sgk toán 9 tập 1 ctst

Cho tam giác OPQ vuông tại O có P = 39^o và PQ = 10 cm. Hãy giải tam giác vuông OPQ.

Lời giải rút gọn:

Ta có OP = 10.cos 39^o = 7,77 cm

OQ = 10. sin 39^o = 6,29 cm

Q = 90^o – 39^o = 51^o 

Giải rút gọn bài 15 trang 73 sgk toán 9 tập 1 ctst

Hai điểm P và Q cách nhau 203 m và thẳng hàng với chân của một toà tháp (Hình 3). Từ đỉnh của toà tháp đó, một người nhìn thấy hai điểm P, Q với hai góc nghiêng xuống lần lượt là 38^o và 44^o. Tính chiều cao của toà tháp

Lời giải rút gọn:

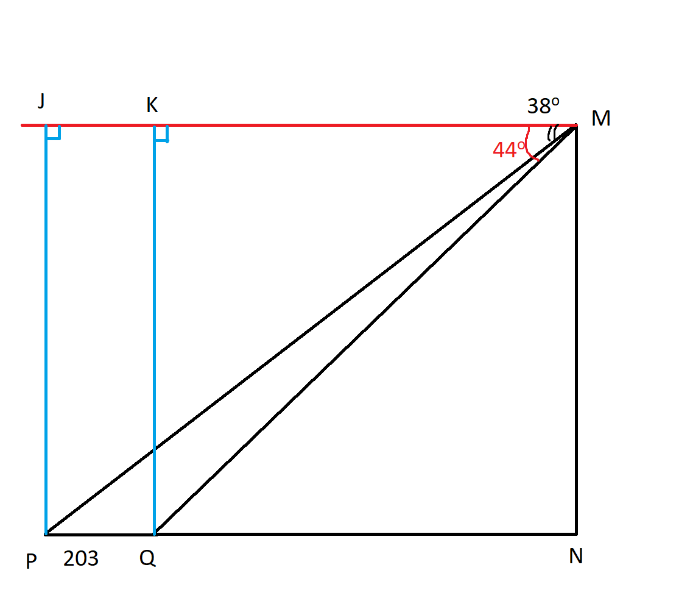
Từ P và Q ta kẻ 2 đường thẳng vuông góc xuông đường thẳng M ta được tam giác MJP vuông tại J và MKQ vuông tại K.

Xét tam giác MJP ta có:

tan JMP =

ó tan 38^o = (1)

Xét tam giác MKQ ta có:

tan KMQ =

ó tan 44^o = (2)

Từ (1) và (2) ta có MN = tan 38^o .(203 + QN) = tan 44^o.QN

ó tan 38^o .(203 + QN) = tan 44^o.QN

ó 203 + QN =

ó QN = 860,07 m

Xét tam giác QMN vuông tại N ta có QMN = 90^o – 44^o = 46^o

=> MN = QN . cot 46^o = 890,62 m

Vậy toà tháp cao 890,62 m

Giải rút gọn bài 16 trang 73 sgk toán 9 tập 1 ctst

Hai chiếc tàu thuỷ B và C cùng xuất phát từ một vị trí A, đi thẳng theo hai hướng tạo thành một góc 60° (Hình 4). Tàu B chạy với tốc độ 20 hải lí/giờ, tàu C chạy với tốc độ 15 hải lí/giờ. Hỏi sau 1,5 giờ hai tàu B và C cách nhau bao nhiêu hải lí (kết quả làm tròn đến hàng phần trăm)?

Lời giải rút gọn:

Sau 1,5 giờ tàu B chạy được quãng đường là AB = 20.1,5 = 30 hải lí

Sau 1,5 giờ tàu C chạy được quãng đường là AC = 15.1,5 = 22,5 hải lí

Áp dụng định lý hàm Cos ta có

BC² = AB² + AC² – 2.AB.AC.cos BAC

ó BC = 27,05

Vậy sau 1,5 giờ tàu B cách tàu C là 27,05 hải lí