Slide bài giảng Toán 9 Chân trời bài 2: Hệ thức giữa cạnh và góc của tam giác vuông

Tóm lược nội dung

BÀI 2. HỆ THỨC GIỮA CẠNH VÀ GÓC CỦA TAM GIÁC VUÔNG

1. HỆ THỨC GIỮA CẠNH VÀ GÓC CỦA TAM GIÁC VUÔNG

Giải rút gọn hoạt động 1 trang 67 sgk toán 9 tập 1 ctst

Cho tam giác ABC vuông tại A (Hình 1).

a) Hãy tính sin B theo b và a, cos B theo c và a. Sử dụng các kết quả tính được để giải thích tại sao ta lại có các đẳng thức: b = a. sin B; c = a. cos B.

b) Hãy tính tan B theo b và c, cot B theo c và b. Sử dụng các kết quả tính được ở trên để giải thích tại sao ta lại có các đẳng thức: b = c. tan B; c = b. cot B.

Lời giải rút gọn:

a) sin B = b / a

=> b = a . Sin B

; cos B = c / a

=> c = a . cos B 

b) tan B = b / c 

=> b = c .tan B

cot B = c / b

=> c = cot B . b

Giải rút gọn thực hành 1 trang 68 sgk toán 9 tập 1 ctst

Cho tam giác ABC vuông tại A có độ dài cạnh huyền bằng 20 cm. Tính độ dài các cạnh góc vuông trong mỗi trường hợp sau (kết quả làm tròn đến hàng phần trăm):

a) B=36°;

b) C=41°.

Lời giải rút gọn:

a) AC = 20.sin(36^o)  = 11,76 cm 

AB = 20.cos(36^o) = 16,18 cm

b) AB = 20.sin(41^o) = 13,12 cm

AC = 15,09 cm

Giải rút gọn thực hành 2 trang 68 sgk toán 9 tập 1 ctst

Tính độ dài cạnh góc vuông x của mỗi tam giác vuông trong hình 3.

Lời giải rút gọn:

a) x = 9.cot (32^o) = 14,4

b) x  = 5.tan(48^o)  = 5,55

Giải rút gọn vận dụng 1 trang 68 sgk toán 9 tập 1 ctst

Một cần cẩu đang nâng một khối gỗ trên sông. Biết tay cầu AB có chiều dài là 16 m và nghiêng một góc 42° so với phương nằm ngang (Hình 4). Tính chiều dài BC của đoạn dây cáp (kết quả làm tròn đến hàng phần mười).

Lời giải rút gọn:

BC = AB.sin(42^o) = 10,7 m

2. GIẢI TAM GIÁC VUÔNG

Giải rút gọn hoạt động 2 trang 69 sgk toán 9 tập 1 ctst

Cho tam giác ABC(Hình 5). Em hãy cho biết trong các trường hợp nào sau đây, ta có thể tính được tất cả các cạnh và góc của tam giác. Giải thích cách tính.

Lời giải rút gọn:

Giải rút gọn vận dụng 2 trang 70 sgk toán 9 tập 1 ctst

Trong hình 9, cho OH = 4m; AOH = 45^o, HOB = 28^o. Tính chiều cao AB của cây

Lời giải rút gọn:

AH = 4.tan(42^o) = 3,6 m

HB = 4.tan(28^o) = 2,12 m

=> AB = AH + HB = 5,72 m

3. GIẢI BÀI TẬP CUỐI SÁCH

Giải rút gọn bài 1 trang 71 sgk toán 9 tập 1 ctst

Tính các cạnh của hình chữ nhật ABCD. Biết AC = 16 cm và BAC = 68^o (Hình 10)

Lời giải rút gọn:

AD = BC = 16.tan(68^o) = 39,6 cm

AB = DC = 16.cot(68^o) = 6,46 cm

Giải rút gọn bài 2 trang 71 sgk toán 9 tập 1 ctst

Cho tam giác ABC có BC = 20 cm, ABC = 22°, ACB = 30°.

a) Tính khoảng cách từ điểm B đến đường thẳng AC.

b) Tính các cạnh và các góc còn lại của tam giác ABC.

c) Tính khoảng cách từ điểm A đến đường thẳng BC.

Lời giải rút gọn:

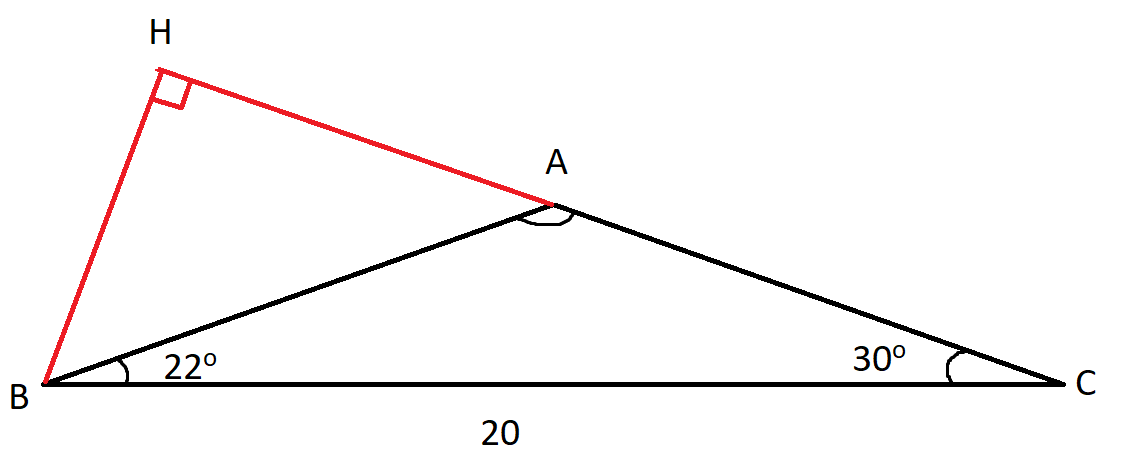
a) Từ B ta kẻ vuông góc xuống AC ta được AH

Trong tam giác HBC vuông tại H ta có BC = 20 cm

=> BH = 20.sin(30^o) = 10 cm

Vậy khoảng cách từ điểm B đến đường thẳng AC là 10 cm

b) Trong tam giác ABC ta có BAC = 128^o

=> Góc kề HAB = 180^o – BAC = 52^o

Mà sin HAB = BH / AB

=> AB = BH / sin HAB = BH / sin(52^o)  = 10 / sin(52^o) = 12,69 cm

Ta có AH = AB . cos HAB = AB . cos(52^o) = 7,81 cm

Lại có HC = 20.cos HCB = 20. cos(30^o) = 10 cm

=> AC = HC – AH = 9,51 cm

Vậy cạnh còn lại trong tam giác là AB = 12,69 cm, AC = 9,51 cm và góc BAC = 128^o

c) 

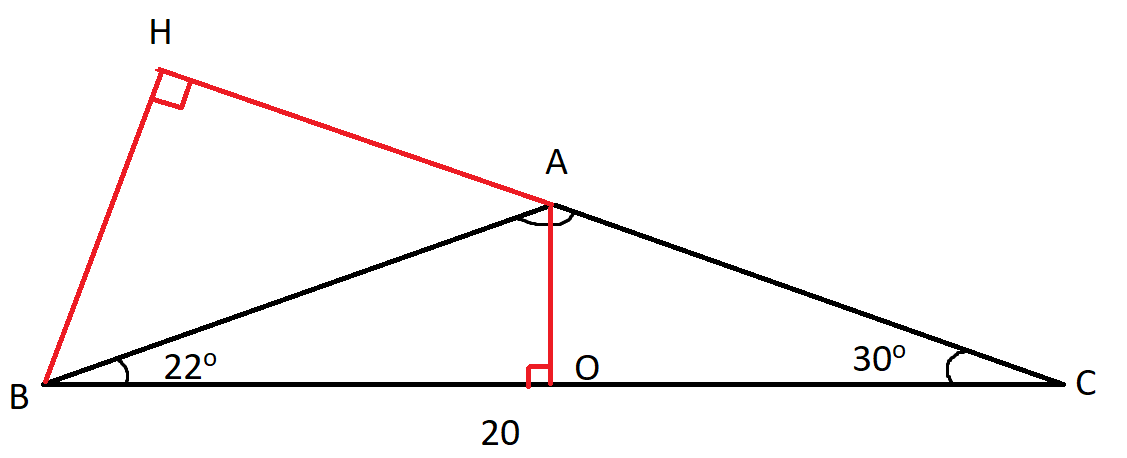
Từ A kẻ vuông góc xuông BC ta có AO

Trong tam giác AOC vuông tại O ta có

AO = AC.sin ACO = AC.sin(30^o) = 4,755 cm

Vậy khoảng cách từ A đến BC là 4,755 cm

Giải rút gọn bài 3 trang 71 sgk toán 9 tập 1 ctst

Một người đẩy một vật lên hết một con dốc nghiêng 35^o(Hình 11). Tính độ cao của vật so với mặt đất biết con dốc là 4m

Lời giải rút gọn:

Gọi chiều cao con dốc là h (m)

Ta có h = 4.sin(35^o) = 2,29 (m)

Giải rút gọn bài 4 trang 71 sgk toán 9 tập 1 ctst

Lúc 6 giờ sáng, bạn An đi xe đạp từ nhà (điểm A) đến trường (điểm B). Khi đi từ A đến B, An phải đi đoạn lên dốc AC và đoạn xuống dốc CB (Hình 12). Biết AB = 762 m, A = 6°, B=4°.

a) Tính chiều cao h của con dốc.

b) Hỏi bạn An đến trường lúc mấy giờ? Biết rằng tốc độ khi lên dốc là 4 km/h và tốc độ khi xuống dốc là 19 km/h.

Lời giải rút gọn:

a) Ta có tan ACH =

Lại có tan BCH =

Mà

 HC = 762 : (9,51 + 14,3) = 32

=> h = 32

b) Ta có

=> AC = = 306,13 (m) = 0,306 (km)

Tương tự ta có BC = 0,458 (km)

Thời gian mất khi đi lên dốc là: t = s / v = 0,306 / 4 = 0,0765 (giờ)

Thời gian mất khi đi xuống dốc là: t = s / v = 0,458 / 19 = 0,024 (giờ)

=> Sau khi đến trường là: 6 + 0,0765 + 0,024 = 6,1005 (giờ) = 6 giờ 6 phút