Slide bài giảng Toán 9 Chân trời bài 3: Góc ở tâm, góc nội tiếp

Tóm lược nội dung

BÀI 3. GÓC Ở TÂM. GÓC NỘI TIẾP

1. GÓC Ở TÂM

Giải rút gọn hoạt động 1 trang 90 sgk toán 9 tập 1 ctst

Cho hai điểm A, B trên đường tròn (O; R). Nêu nhận xét về đỉnh và cạnh của AOB.

Lời giải rút gọn:

OA = OB = R

Đỉnh trùng với tâm O của đường tròn

Giải rút gọn thực hành 1 trang 90 sgk toán 9 tập 1 ctst

Tính số đo góc ở tâm EOA và AOB trong Hình 3. Biết AC và BE là 2 đường kính của đường tròn (O)

Lời giải rút gọn:

Ta có EOA = COB = 57^o

Ta có  AOB = 360^o – COB – AOE – DOE – COB = 360^o – 57^o – 57^o – 28^o – 95^o = 123^o

Giải rút gọn vận dụng 1 trang 91 sgk toán 9 tập 1 ctst

Tính số đo góc ở tâm được tạo thành khi kim giờ quay:

a) Từ 7 giờ đến 9 giờ

b) Từ 9 giờ đến 12 giờ

Lời giải rút gọn:

a) 60^o

b) 90^o

2. CUNG, SỐ ĐO CUNG

Giải rút gọn hoạt động 2 trang 91 sgk toán 9 tập 1 ctst

Vẽ vào vở đường tròn (O) và hai điểm A, B nằm trên (O). Dùng bút chì khác màu tô hai phần của đường tròn được bân chia bởi 2 điểm A và B

Lời giải rút gọn:

Giải rút gọn hoạt động 3 trang 91 sgk toán 9 tập 1 ctst

Cho OA và OB là hai bán kính vuông góc với nhau của đường tròn (O), C là điểm trên cung nhỏ AB (Hình 7). Ta coi số đo của một cung nhỏ là số đo của góc ở tâm chắn cung đó.

a) Xác định số đo của cung AB.

b) So sánh số đo của hai cung AC và AB.

Lời giải rút gọn:

a) Số đo cung AB là 90^o

b) AC < AB

Giải rút gọn thực hành 2 trang 92 sgk toán 9 tập 1 ctst

Cho đường tròn (O) có hai đường kính AB và CD vuông góc với nhau (Hình 9). Xác định số đo của các cung AB, AC và AD.

Lời giải rút gọn:

Số đo cung AB là 90^o

Số đo cung AC là 90^o

Số đo cung AD là 90^o

Giải rút gọn vận dụng 2 trang 92 sgk toán 9 tập 1 ctst

Xác định số đo cung AB trong hình ngôi sao năm cánh (Hình 10)

Lời giải rút gọn:

Số đo cung AB < 90^o

Giải rút gọn hoạt động 4 trang 92 sgk toán 9 tập 1 ctst

Trên đường tròn (O), vẽ hai cung nhỏ AB, BC sao cho AOB = 18°, BOC = 32° và tia OB ở giữa hai tia OA, OC (Hình 11). Tính số đo của các cung AB, BC, AC.

Lời giải rút gọn:

Số đo cung AB là 18^o và 342^o

Số đo cung BC là 32^o và 328^o

Số đo cung AC là 50^o và 310^o

Giải rút gọn thực hành 3 trang 93 sgk toán 9 tập 1 ctst

Trên cung AB có số đo 90^o của đường tròn (O), lấy điểm M sao cho cung AM có số đo 15^o. Tính số đo cung MB

Lời giải rút gọn:

Nếu tia MO nằm giữa AO và OB

=> Cung MB có số đo là 90^o – 15^o = 75^o

Nếu tia MO nằm ngoài tia AO và OB

=> Cung MB có số đo là 360^o – 90^o – 15^o = 255^o

Giải rút gọn vận dụng 3 trang 92 sgk toán 9 tập 1 ctst

Bạn Hùng làm một cái diều với thân diều là hình tứ giác SAOB sao cho OS là đường phân giác của AOB và ASB=106°. Thanh tre màu xanh lá được uốn cong thành cung AB của đường tròn tâm O và SA, SB là hai tiếp tuyến của (O) (Hình 12). Tính số đo của AB.

Lời giải rút gọn:

Số đo cung AB là 108^o và 252^o

3. GÓC NỘI TIẾP

Giải rút gọn hoạt động 5 trang 92 sgk toán 9 tập 1 ctst

Giải các phương trình:

Hãy cho biết trong các góc APB, АОВ, AMB, AQB, góc nào có đỉnh nằm trên đường tròn (O).

Lời giải rút gọn:

Các góc APB, АОВ, AMB có đỉnh nằm trên đường tròn (O)

Giải rút gọn thực hành 4 trang 92 sgk toán 9 tập 1 ctst

Cho tam giác đều MNP có ba đỉnh nằm trên đường tròn (I). Hãy chỉ ra các góc nội tiếp của đường tròn (1) và tính số đo của các góc nội tiếp đó. 

Lời giải rút gọn:

Các góc nội tiếp của đường tròn (I) là các góc nội tiếp của tam giác MNP, và mỗi góc này đều có số đo là 120^o.

Giải rút gọn vận dụng 4 trang 92 sgk toán 9 tập 1 ctst

Cho hai điểm E và F nằm trên đường tròn (O). Có bao nhiêu góc nội tiếp chắn cung EF

Lời giải rút gọn:

Có 2 góc nội tiếp chắn cung EF

Giải rút gọn hoạt động 6 trang 93 sgk toán 9 tập 1 ctst

Quan sát Hình 15. Ta có góc nội tiếp AMB chẳn cung AB trên đường tròn (O). Cho biêt AOB = 60°.

a) Tính số đo AB.

b) Dùng thước đo góc để tìm số đo AMB.

c) Có nhận xét gì về hai số đo của AMB và AB?

Lời giải rút gọn:

a) Vì góc nội tiếp AMB chắn cung AB trên đường tròn (O), nên số đo của góc nội tiếp AMB là gấp đôi số đo của cung AB. Do đó, AMB = 2.AOB = 2.60^o = 120^o

b) Sử dụng thước đo góc và đặt thước đo lên AB sao cho một cạnh của thước đo trùng với AB và cạnh kia của thước đo trùng với AM hoặc MB. Khi đó, số đo của góc AMB chính là số đo đo được trên thước đo góc.

c) Hai số đo của AMB và AB có mối quan hệ là góc nội tiếp AMB chắn cung AB trên đường tròn. Do đó, số đo của góc AMB luôn gấp đôi số đo của cung AB.

Giải rút gọn thực hành 5 trang 96 sgk toán 9 tập 1 ctst

Cho ba điểm A, B, C nằm trên đường tròn (O) sao cho AOB = 50°, BOC = 30°, điểm B thuộc cung nhỏ AC. Gọi M, N lần lượt là hai điểm trên hai cung nhỏ AB, AC và chia mỗi cung đó thành hai cung bằng nhau. Tìm số đo các góc sau:

a) BCA, BAC;

b) MBA, BAN.

Lời giải rút gọn:

a) 

- Ta có BCA =

- Góc nội tiếp chắn cùng có số đo bằng gấp đôi số đo của cung mà chúng chắn. Do đó,

b) 

- Ta chia mỗi cung nhỏ thành hai cung bằng nhau, do đó, các cung này có số đo là 

- MBA = 165^o

- BAN = 165^o vì N nằm trên cung nhỏ AC.

Vậy:

a) BCA = 15^o và BAC = 100^o

b) MBA = 165^o và BAN = 165^o

Giải rút gọn vận dụng 5 trang 96 sgk toán 9 tập 1 ctst

Một huấn luyện viên cho cầu thủ tập sút bóng vào cầu môn MN (Hình 20). Nếu bóng được đặt ở điểm X thì MXN gọi là góc sút từ vị trí X. Hãy so sánh các góc sút MXN, MYN, MZN.

Lời giải rút gọn:

- 3 góc bằng nhau vì cùng chắn một cung MN

 4. GIẢI BÀI TẬP CUỐI SÁCH

Giải rút gọn bài 1 trang 97 sgk toán 9 tập 1 ctst

Cho đường tròn (O; 5 cm) và điểm M sao cho OM = 10 cm. Qua M vẽ hai tiếp tuyến với đường tròn tại A và B. Tính số đo góc ở tâm được tạo bởi hai tia OA và OB.

Lời giải rút gọn:

Xét tam giác OAM vuông tại A

Ta có cos MOA = 5 / 10 = 1 / 2 

=> MOA = 60^o

Mà AOB = 2MOA = 120^o

Giải rút gọn bài 2 trang 97 sgk toán 9 tập 1 ctst

Cho tam giác đều ABC. Vẽ đường tròn đường kính BC cắt cạnh AB và AC lần lượt tại D và E. Hãy so sánh các cung BD, DE, EC

Lời giải rút gọn:

Các cung BD, DE và EC đều bằng nhau trong tam giác đều ABC.

Giải rút gọn  bài 3 trang 97 sgk toán 9 tập 1 ctst

Dây cung AB chia đường tròn (O) thành hai cung. Cung lớn có số đo bằng ba lần cung nhỏ.

a) Tính số đo mỗi cung.

b) Chứng minh khoảng cách OH từ tâm O đến dây cung AB có độ dài bằng AB/2

Lời giải rút gọn:

a) Gọi số đo của cung nhỏ là \( x \) đơn vị đo, khi đó số đo của cung lớn là 3x đơn vị đo.

Vì cung lớn có số đo gấp ba lần cung nhỏ, nên ta có:

3x = x + 180^o

x = 180^o / 2 = 90^o

Vậy, số đo của cung nhỏ là 90^o và số đo của cung lớn là 3.90^o = 270^o

b) Gọi H là điểm chiếu vuông góc của O lên AB. Khoảng cách từ O đến H là bán kính của đường tròn.

Vì AB là dây cung, nên OH là phân giác của góc AOB. Vậy, ta có:

OHA = OBA = ½ . số đo của cung lớn = ½ . 270^o = 135^o

Vì tam giác OHA là tam giác vuông tại H, ta có: tan(∠OHA)=  OH / AH​

Tuy nhiên, vì OHA=135∘ và OH là bán kính của đường tròn, ta có thể tính OH. Vì OH là bán kính, nên OH=R, trong đó R là bán kính của đường tròn.

AH=OH×tan(∠OHA)=R×tan(135∘)

Nhưng tan(135∘)= -1 , do đó AH=−R.

OH = |AH| = |-R| = R

Vậy, ta thấy rằng khoảng cách từ tâm O đến dây cung AB có độ dài bằng bán kính của đường tròn R, hay OH = R. Do đó, OH = AB/2

Giải rút gọn bài 4 trang 97 sgk toán 9 tập 1 ctst

Kim giờ và kim phút của đồng hồ tạo thành một góc ở tâm có số đo là bao nhiêu vào những thời điểm sau?

a) 2 giờ

b) 8 giờ

c) 21 giờ

Lời giải rút gọn:

a) 60°,

b) 240°,

c) 270°.

Giải rút gọn bài 5 trang 97 sgk toán 9 tập 1 ctst

Cho hai đường tròn đồng tâm (O; R) và (O; ). Một tiếp tuyến của đường tròn nhỏ cắt đường tròn lớn tại hai điểm A và B. Tính số đo cung AB

Lời giải rút gọn:

Gọi điểm I là điểm tiếp tuyến của đường tròn (O;R) với AB

Xét tam giác AIO vuông tại I

cos AOI =  : R=

=> AOI = 30^o

Mà AOB = 2.AOI = 2.30^o = 60^o

Giải rút gọn bài 6 trang 97 sgk toán 9 tập 1 ctst

Xác định số đo các cung AB, BC, CA trong mỗi hình sau.

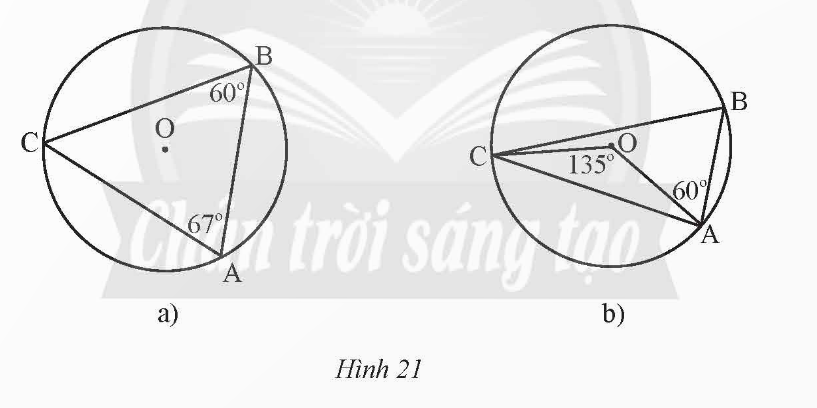
Lời giải rút gọn:

a) Số đo cung AB là 53^o

Số đo cung BC là 67^o

Số đo cung CA là 60^o

b) a) Số đo cung AB là  52,5^o

Số đo cung BC là 60^o

Số đo cung CA là 67,5^o

Giải rút gọn bài 7 trang 97 sgk toán 9 tập 1 ctst

Cho đường tròn (O) có hai đường kính AB, CD vuông góc với nhau. Lấy một điểm M trên cung nhỏ AC rồi vẽ tiếp tuyến với đường tròn (O) tại M. Tiếp tuyến này cắt đường thẳng CD tại S. Chứng minh rằng MSD = 2MBA.

Lời giải rút gọn:

Gọi P là giao điểm của AB và CD.

Vì AB và CD là hai đường kính của đường tròn O và vuông góc với nhau, nên AB và CD là hai đường phân giác của nhau.

Vậy, ta có: MA = MB và SA = SD (do MS là tiếp tuyến của đường tròn, nên MA và SA là hai phân giác của góc MSD).

Ngoài ra, vì AB và CD là đường kính, nên góc BAP và DPS là góc vuông.

Do đó, các tam giác BAP và DPS là tam giác vuông cân, với BP = DP.

• MBA = MAB = MSD 

BAP =  DPS (góc vuông),

BP = DP (do AB) và CD là đường kính cùng vuông góc).

Vậy, ta đã chứng minh được MSD đồng dạng với MBA.

Do đó, MSD = 2MBA.