Slide bài giảng Toán 9 Chân trời bài 1: Hàm số và đồ thị của hàm số y = ax^2 (a ≠ 0)
Slide điện tử bài 1: Hàm số và đồ thị của hàm số y = ax^2 (a ≠ 0). Kiến thức bài học được hình ảnh hóa, sinh động hóa. Trình bày với các hiệu ứng hiện đại, hấp dẫn. Giúp học sinh hứng thú học bài. Học nhanh, nhớ lâu. Có tài liệu này, hiệu quả học tập của học môn Toán 9 Chân trời sáng tạo sẽ khác biệt
Bạn chưa đủ điều kiện để xem được slide bài này. => Xem slide bài mẫu
Tóm lược nội dung
BÀI 1. HÀM SỐ VÀ ĐỒ THỊ CỦA HÀM SỐ y = ax2 (a  0)
0)
KHỞI ĐỘNG
Một vật được thả rơi tự do từ độ cao 45 m. Quãng đường chuyển động s (m) của vật theo thời gian rơi t (giây) được cho bởi công thức s = 5t2. Sau khi thả 2 giây, quãng đường vật di chuyển được là bao nhiêu mét?
Giải rút gọn:
s = 5t2 = 5.22 = 20 (m).
1. HÀM SỐ y = ax2 (a 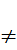 0)
0)
Giải rút gọn hoạt động 1 trang 6 sgk toán 9 tập 2 ctst
Diện tích S của hình tròn được tính bởi công thức S = ![]() R2, trong đó R là bán kính hình tròn và
R2, trong đó R là bán kính hình tròn và ![]() 3,14.
3,14.
a) Tính diện tích của hình tròn với R = 10 cm.
b) Diện tích S có phải là hàm số của biến không?
Giải rút gọn:
a) S = ![]() R2 =
R2 = ![]() .102
.102![]() 314,16 cm2.
314,16 cm2.
b) Diện tích S là hàm số của biến số R.
Giải rút gọn thực hành 1 trang 7 sgk toán 9 tập 2 ctst
a) Xác định hệ số của x2 trong các hàm số sau: y = 0,75x2; y = –3x2; y = ![]() x2.
x2.
b) Với mỗi hàm số đã cho ở câu a), tính giá trị của y khi x = –2; x = 2.
Giải rút gọn:
a) Các hệ số của x2 lần lượt là: 0,75; –3; ![]() .
.
b) - Thay x = –2 vào hàm số của y = 0,75x2 có: y = 0,75.(–2)2 = 3.
- Thay x = 2 vào hàm số của y = 0,75x2 có: y = 0,75.(2)2 = 3.
- Thay x = –2 vào hàm số của y = –3x2 có: y = –3.(–2)2 = –12.
- Thay x = 2 vào hàm số của y = –3x2 có: y = –3.(2)2 = –12.
- Thay x = –2 vào hàm số của y = ![]() x2 có: y =
x2 có: y = ![]() .(–2)2 = 1.
.(–2)2 = 1.
- Thay x = 2 vào hàm số của y = ![]() x2 có: y =
x2 có: y = ![]() .(2)2 = 1.
.(2)2 = 1.
Giải rút gọn vận dụng 1 trang 7 sgk toán 9 tập 2 ctst
Gọi x (cm) là chiều dài cạnh của một viên gạch lát nền hình vuông.
a) Viết công thức tính diện tích S (cm2) của viên gạch đó.
b) Tính S khi x = 20, x = 30, x= 60.
Giải rút gọn:
a) Công thức tính diện tích: S = x2 (cm2).
b) - Khi x = 20 thì S = 202 = 400 (cm2).
- Khi x = 30 thì S = 302 = 900 (cm2).
- Khi x = 60 thì S = 602 = 3600 (cm2).
2. BẢNG GIÁ TRỊ CỦA HÀM SỐ y = ax2 (a 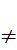 0)
0)
Giải rút gọn hoạt động 2 trang 7 sgk toán 9 tập 2 ctst
Cho hàm số y = = ![]() x2. Hoàn thành bảng giá trị sau:
x2. Hoàn thành bảng giá trị sau:
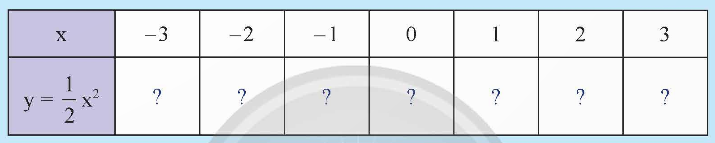
Để lập bảng giá trị của hàm số y = ax2 (a ![]() 0), ta lần lượt cho x nhận các giá trị x1, x2, x3, … ( x1, x2, x3, … tăng dần) và tính các giá trị tương ứng của y rồi ghi vào bảng sau:
0), ta lần lượt cho x nhận các giá trị x1, x2, x3, … ( x1, x2, x3, … tăng dần) và tính các giá trị tương ứng của y rồi ghi vào bảng sau:

Giải rút gọn:
x | –3 | –2 | –1 | 0 | 1 | 2 | 3 |
y = = |
| 1 |
| 0 |
| 1 |
|
Giải rút gọn thực hành 2 trang 8 sgk toán 9 tập 2 ctst
Lập bảng giá trị của hai hàm số y = ![]() x2 và y = –
x2 và y = – ![]() x2 với x lần lượt bằng -4; -2; 0; 2; 4.
x2 với x lần lượt bằng -4; -2; 0; 2; 4.
Giải rút gọn:
Bảng giá trị của hàm số y = ![]() x2
x2
x | –4 | –2 | 0 | 2 | 4 |
y = | 4 | 1 | 0 | 1 | 4 |
Bảng giá trị của hàm số y = – ![]() x2
x2
x | –4 | –2 | 0 | 2 | 4 |
y = – | –4 | –1 | 0 | –1 | –4 |
Giải rút gọn vận dụng 2 trang 8 sgk toán 9 tập 2 ctst
Một vật rơi tự do từ độ cao 125 m so với mặt đất. quãng đường chuyển động s (m) của vật phụ thuộc vào thời gian t (giây) được cho bởi công thức s = 5t2.
a) Sau 2 giây, vật này cách mặt đất bao nhiêu mét? Tương tự, sau 3 giây vật này cách mặt đất bao nhiêu mét?
b) Sao bao lâu thì vật này tiếp đất?
Giải rút gọn:
a) - Sau 2 giây, vật đi được quãng đường là:
s = 5t2 = 5.22 = 20 (m).
Sau 2 giây, vật này cách mặt đất: s1 = 125 – 20 = 105 (m).
- Sau 3 giây, vật đi được quãng đường là:
s’ = 5t2 = 5.32 = 45 (m).
Sau 2 giây, vật này cách mặt đất: s2 = 125 – 45 = 80 (m).
b) Thời gian để vật tiếp đất tiếp đất là:
125 = 5t2 ![]() t = 5 (giây) (thỏa mãn) hoặc t = –5 (loại vì t > 0).
t = 5 (giây) (thỏa mãn) hoặc t = –5 (loại vì t > 0).
3. ĐỒ THỊ CỦA HÀM SỐ y = ax2 (a  0)
0)
Giải rút gọn hoạt động 3 trang 8 sgk toán 9 tập 2 ctst
Cho hàm số y = x2. Ta lập bảng giá trị sau:

Từ bảng trên, ta lấy các điểm A(-3; 9), B(-2; 4), C(-1; 1), O(0; 0), C’(1; 1), B’(2; 4), A’(3; 9) trên mặt phẳng toạ độ Oxy. Đồ thị của hàm y = x2 là một đường cong đi qua các điểm nêu trên và có dạng như Hình 2.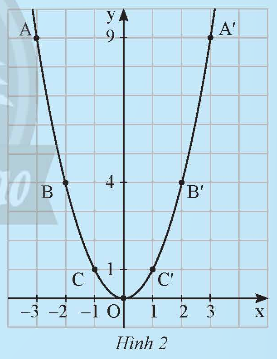
Từ đồ thị Hình 2, hãy trả lời các câu hỏi sau:
a) Đồ thị của hàm số có vị trí như thể nào so với trục hoành?
b) Có nhận xét gì về vị trí của các cặp điểm A và A’, B và B’, C và C’ so với trục tung?
c) Điểm nào là điểm thấp nhất của đồ thị?
Giải rút gọn:
a) Tiếp xúc với trục hoành tại gốc tọa độ O và nằm phía trên trục hoành.
b) Các cặp điểm đó nằm đối xứng với nhau qua trục tung.
c) Điểm O(0; 0).
Giải rút gọn hoạt động 4 trang 8 sgk toán 9 tập 2 ctst
Cho hàm số y = = ![]() x2.
x2.
a) Lập bảng giá trị của hàm số khi x lần lượt nhận các giá trị -2; -1; 0; 1; 2.
b) Vẽ đồ thị của hàm số. Có nhận xét gì về đồ thị hàm số đó?
Giải rút gọn:
a) Bảng giá trị của hàm số y =![]() x2
x2
x | –2 | –1 | 0 | 1 | 2 |
y = | –6 |
| 0 |
| –6 |
b) Đồ thị hàm số của hàm số y =![]() x2
x2
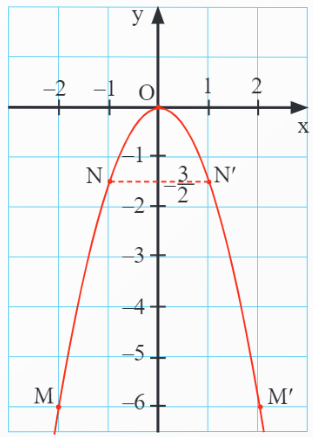
Nhận xét:
- Đồ thị hàm số nằm phía dưới trục hoành và tiếp xúc với trục hoành.
- Các điểm giá trị trên đồ thị nằm đối xứng nhau qua trục tung.
- Điểm điểm cao nhất của đồ thị là gốc O(0; 0).
Giải rút gọn thực hành 3 trang 9 sgk toán 9 tập 2 ctst
Vẽ đồ thị hàm số y = 2x2.
Giải rút gọn:
Bảng giá trị của hàm số y = 2x2
x | –2 | –1 | 0 | 1 | 2 |
y = 2x2 | 8 | 2 | 0 | 2 | 8 |
Đồ thị hàm số của hàm số y = 2x2
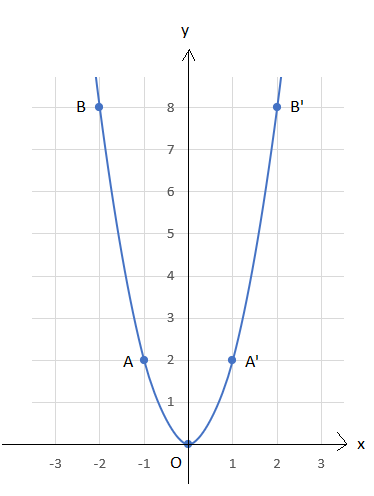
Giải rút gọn vận dụng 3 trang 10 sgk toán 9 tập 2 ctst
Động năng (tính bằng J) của một quả bưởi nặng 1 kg rơi với tốc độ v (m/s) được tính bằng công thức K = ![]() v2.
v2.
a) Tính động năng của quả bưởi đạt được khi nó rơi với tốc độ lần lượt là 3 m/s, 4 m/s.
b) Tính tốc độ rơi của quả bưởi tại thời điểm quả bưởi đạt được động năng 32 J.
Giải rút gọn:
a) - Khi v = 3 m/s thì K = ![]() v2 =
v2 = ![]() .32 =
.32 = ![]() (J).
(J).
- Khi v = 4 m/s thì K = ![]() v2 =
v2 = ![]() .42 = 8 (J).
.42 = 8 (J).
b) Động năng đạt được là 32 J thì ![]() v2 = 32
v2 = 32![]() v2 = 64
v2 = 64
![]() v = 8 (m/s) (thỏa mãn) hoặc v = –8 (loại vì v > 0).
v = 8 (m/s) (thỏa mãn) hoặc v = –8 (loại vì v > 0).
4. GIẢI BÀI TẬP CUỐI SÁCH
Giải rút gọn bài 1 trang 10 sgk toán 9 tập 2 ctst
Cho hàm số y = –x2.
a) Lập bảng giá trị của hàm số. b) Vẽ đồ thị hàm số.
Giải rút gọn:
a) Bảng giá trị của hàm số y = –x2
x | –2 | –1 | 0 | 1 | 2 |
y = –x2 | –4 | –1 | 0 | –1 | –4 |
b) Đồ thị hàm số của hàm số y = –x2
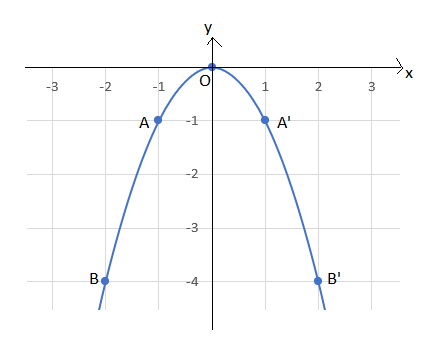
Giải rút gọn bài 2 trang 10 sgk toán 9 tập 2 ctst
Cho hàm số y = = ![]() x2.
x2.
a) Vẽ đồ thị hàm số.
b) Trong các điểm A(-6; -8), B(6; 8), C ![]() , điểm nào thuộc đồ thị hàm số trên?
, điểm nào thuộc đồ thị hàm số trên?
Giải rút gọn:
a) Bảng giá trị của hàm số y = = ![]() x2
x2
x | –4 | –2 | 0 | 2 | 4 |
y = = | 8 | 2 | 0 | 2 | 8 |
Đồ thị hàm số của hàm số y = = ![]() x2
x2
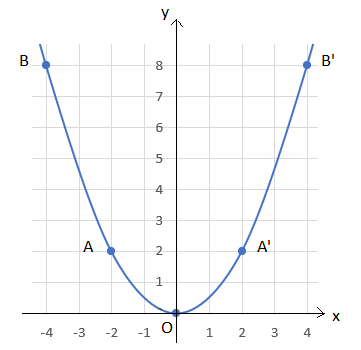
b) - Thay x = –6 vào hàm số của y = = ![]() x2 có: y = =
x2 có: y = = ![]() .(–6)2 = 18
.(–6)2 = 18 ![]() –8.
–8.
![]() A(-6; -8) không thuộc đồ thị hàm số y = =
A(-6; -8) không thuộc đồ thị hàm số y = = ![]() x2.
x2.
- Thay x = 6 vào hàm số của y = = ![]() x2 có: y = =
x2 có: y = = ![]() .(6)2 = 18
.(6)2 = 18 ![]() 8.
8.
![]() B(6; 8) không thuộc đồ thị hàm số y = =
B(6; 8) không thuộc đồ thị hàm số y = = ![]() x2.
x2.
- Thay x = ![]() vào hàm số của y = =
vào hàm số của y = = ![]() x2 có: y = =
x2 có: y = = ![]() .
.![]() =
= ![]() =
= ![]() .
.
![]() C
C ![]() thuộc đồ thị hàm số y = =
thuộc đồ thị hàm số y = = ![]() x2.
x2.
Giải rút gọn bài 3 trang 10 sgk toán 9 tập 2 ctst
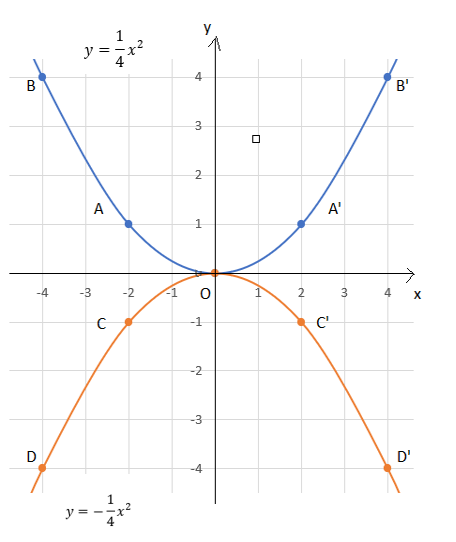
Cho hai hàm số y = ![]() x2 và y = –
x2 và y = – ![]() x2. Vẽ đồ thị của hai hàm số đã cho trên cùng một mặt phẳng tọa độ Oxy.
x2. Vẽ đồ thị của hai hàm số đã cho trên cùng một mặt phẳng tọa độ Oxy.
Giải rút gọn:
Bảng giá trị của hàm số y = ![]() x2
x2
x | –4 | –2 | 0 | 2 | 4 |
y = | 4 | 1 | 0 | 1 | 4 |
Bảng giá trị của hàm số y = – ![]() x2
x2
x | –4 | –2 | 0 | 2 | 4 |
y = – | –4 | –1 | 0 | –1 | –4 |
Đồ thị của hai hàm số trên cùng một mặt phẳng
Giải rút gọn bài 4 trang 10 sgk toán 9 tập 2 ctst
Cho hàm số y = ax2 (a ![]() 0).
0).
a) Tìm a, biết đồ thị hàm số đi qua điểm M(2; 6).
b) Vẽ đồ thị của hàm số với số a vừa tìm được.
c) Tìm các điểm thuộc đồ thị trên có tung độ y = 9.
Giải rút gọn:
a) Thay x = 2; y = 6 vào hàm số ta có:
a.22 = 6 ![]() 4a = 6
4a = 6 ![]() a =
a = ![]()
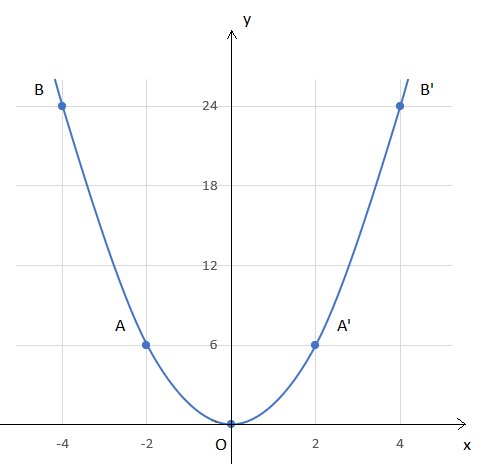
b) Hàm số có dạng y = ![]() x2
x2
Bảng giá trị của hàm số
x | –4 | –2 | 0 | 2 | 4 |
y = | 24 | 6 | 0 | 6 | 24 |
Đồ thị của hàm số y = ![]() x2
x2
c) Khi y = 9, ta có ![]() x2 = 9
x2 = 9 ![]() .
.
![]() Các điểm thuộc đồ thị là: (–
Các điểm thuộc đồ thị là: (–![]() ; 9) và (
; 9) và (![]() ; 9).
; 9).
Giải rút gọn bài 5 trang 10 sgk toán 9 tập 2 ctst
Cho một hình lập phương có độ dài cạnh x (cm).
a) Viết công thức tính diện tích toàn phần S (cm2) của hình lập phương theo x.
b) Lập bảng giá trị của hàm số S khi x lần lượt nhận các giá trị: ![]() ; 1;
; 1; ![]() ; 2; 3.
; 2; 3.
c) Tính độ dài cạnh của hình lập phương, biết S = 54 cm2.
Giải rút gọn:
a) S = 6x2 (cm2)
b) Bảng giá trị của hàm số S = 6x2
x |
| 1 |
| 2 | 3 |
S = 6x2 |
| 6 |
| 24 | 54 |
c) Khi S = 54 cm2 ![]() 6x2 = 54
6x2 = 54 ![]() .
.
Giải rút gọn bài 6 trang 10 sgk toán 9 tập 2 ctst
Khi gió thổi vuông góc vào cánh buồm của một con thuyền thì lực F (N) của nó tỉ lệ thuận với bình phương tốc độ v (m/s) của gió, tức F = av2 (a là hằng số). Biết rằng khi tốc độ của gió bằng 3 m/s thì lực tác động lên cánh buồm bằng 180 N.
a) Tính hằng số a.
b) Với a vừa tìm được, tính lực F khi v = 15 m/s và khi v = 26 m/s.
c) Biết rằng cánh buồm chỉ có thể chịu được một lực tối đa 14580 N, hỏi con thuyền có thể đi được trong gió bão với tốc độ gió 90 km/h hay không?
Giải rút gọn:
a) Vì khi tốc độ của gió bằng 3 m/s thì lực tác động lên cánh buồm bằng 180 N nên thay v = 3 m/s; F = 180 N vào F = av2 ta được:
180 = a.32 ![]() a = 20.
a = 20.
b) Ta có F = 20v2
- Khi v = 15 m/s thì F = 20.152 = 4500 N.
- Khi v = 26 m/s thì F = 20.262 = 13520 N.
c) Đổi 90 km/h = 25 m/s.
Khi con thuyền được trong gió bão với tốc độ gió 25 m/s thì nó chịu một lực có độ lớn: F = 20v2 = 20.252 = 125200 N < 14580 N.
Vậy con thuyền có thể đi được trong gió bão với tốc độ gió 90 km/h.
