Slide bài giảng Toán 9 Cánh diều bài tập cuối chương VI

Tóm lược nội dung

BÀI TẬP CUỐI CHƯƠNG VI

Giải rút gọn bài 1 trang 66 sgk toán 9 tập 2 cánh diều:

Người ta tiến hành phỏng vấn 40 người về một mẫu sản phẩm mối. Người điều tra yêu cầu mỗi người được phỏng vấn cho điểm mẫu sản phẩm đó theo thang điểm là 100. Kết quả thống kê như sau:

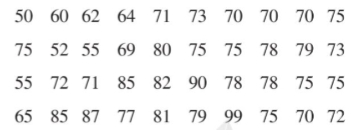
Ghép các số liệu trên thành năm nhóm sau:

[50; 60), [60; 70), [80; 90), [90; 100).

a) Tần số ghép nhóm của nhóm [70; 80) là:

A. 20                     B. 21                      C. 22            D.23

b) Tần số tương đối ghép nhóm của nhóm [50; 60) là:

A. 10%                  B. 12,5%               C. 5%          D. 15%

Lời giải rút gọn:

a) Chọn đáp án D 

b) Chọn đáp án A vì .

Giải rút gọn bài 2 trang 66 sgk toán 9 tập 2 cánh diều:

Một hộp có 25 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 2, 4, 6, …, 48, 50; hai thẻ khác nhau thì ghi hai số khác nhau. 

Rút ngẫu nhiên một thả trong hộp. Xác suất của biến cố “Số xuất hiện trên thẻ được rút ra là số nhỏ hơn 26” là:

A.                     B.                     C.           D.

Lời giải rút gọn:

Chọn đáp án C vì:

- Có 25 kết quả có thể xảy ra.

- Kết quả thuận lợi cho biến cố = (24 - 2):2 + 1 = 12. => .

Giải rút gọn bài 3 trang 66 sgk toán 9 tập 2 cánh diều:

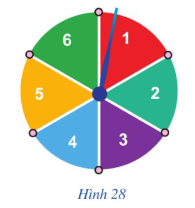
Hình 28 mô tả một đĩa tròn bằng bìa cứng được chia làm sáu phần bằng nhau và ghi các số 1, 2, 3, 4, 5, 6; chiếc kim được gắn cố định vào trục quay ở tâm của đĩa. Quay đĩa tròn và ghi lại số ở hình quạt mà chiếc kim chỉ vào khi đĩa dừng lại. Mẫu số liệu dưới đây ghi lại số liệu sau 40 lần quay đĩa tròn:

a) Trong 40 số liệu thống kê ở trên, có bao nhiêu giá trị khác nhau?

b) Tìm tần số của mỗi giá trị đó.

Lập bảng tần số của mẫu số liệu thống kê đó.

Vẽ biểu đồ tần số ở dạng biểu đồ cột của mẫu số liệu thống kê đó.

c) Tìm tần số tương đối của mỗi giá trị đó.

Lập bảng tần số tương đối của mẫu số liệu thống kê đó.

Vẽ biểu đồ tần số tương đối ở dạng biểu đồ cột và biểu đồ hình quạt tròn của mẫu số liệu thống kê đó.

Lời giải rút gọn:

a) 6

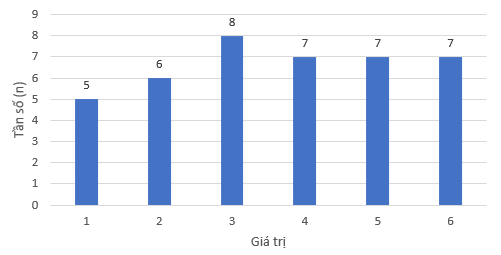
b) Trong số 40 số liệu thống kê, có: 5 lần quay vào số 1, 6 lần quay vào số 6, 8 lần quay vào số 3, 7 lần quay vào số 4, 7 lần quay vào số 5 và 7 lần quay vào số 6.

Bảng tần số:

Biểu đồ dạng cột:

c) 

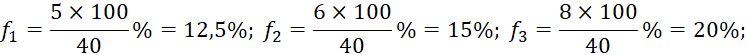
Bảng tần số tương đối:

Biểu đồ dạng cột:

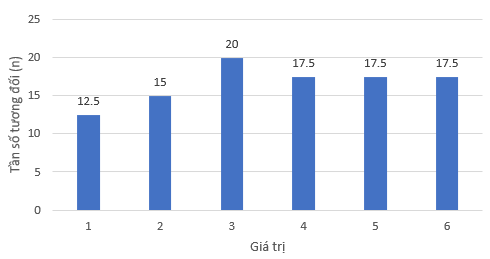
Biểu đồ dạng quạt tròn:

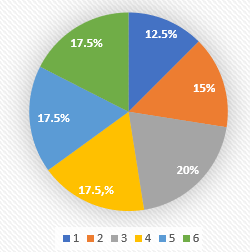
Giải rút gọn bài 4 trang 66 sgk toán 9 tập 2 cánh diều:

Sau khi thống kê độ dài (đơn vị: centimét) của 50 cây con ở vườn thí nghiệm, người ta nhận được bảng tần số tương đối ghép nhóm như sau:

Vẽ biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ cột và biểu đồ đoạn thẳng của mẫu số liệu ghép nhóm ở Bảng 38.

Lời giải rút gọn:

Biểu đồ cột:

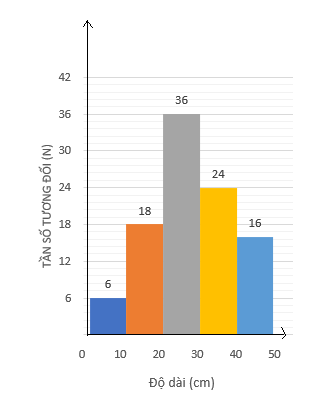
Biểu đồ đoạn thẳng:

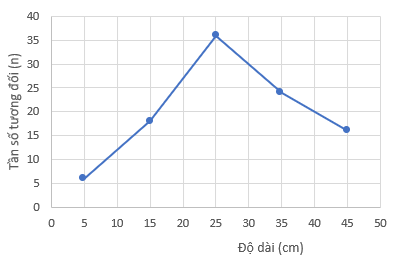
Giải rút gọn bài 5 trang 67 sgk toán 9 tập 2 cánh diều:

Mẫu số liệu dưới đây ghi lại độ dài quãng đường di chuyển trong một tuần (đơn vị: kilômét) của 60 chiếc ô tô:

Ghép các số liệu trên thành năm nhóm sau:

[100 ; 120), [120 ; 140), [140 ; 160), [160 ; 180), [180 ; 200).

a) Tìm tần số của mỗi nhóm đó.

Lập bảng tần số ghép nhóm của mẫu số liệu ghép nhóm đó.

b) Tìm tần số tương đối của mỗi nhóm đó.

Lập bảng tần số tương đối ghép nhóm của mẫu số liệu ghép nhóm đó.

Vẽ biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ cột và biểu đồ đoạn thẳng của mẫu số liệu ghép nhóm đó.

Lời giải rút gọn:

a) Các nhóm [100 ; 120), [120 ; 140), [140 ; 160), [160 ; 180), [180 ; 200) lần lượt có tần số là: n₁ = 6, n₂ = 15, n₃ = 27, n₄ = 9, n₅ = 3.

Bảng tần số ghép nhóm:

b) 

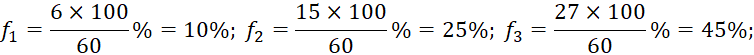
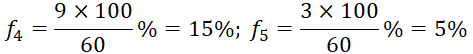
Bảng tần số tương đối ghép nhóm:

Biểu đồ dạng đường thẳng:

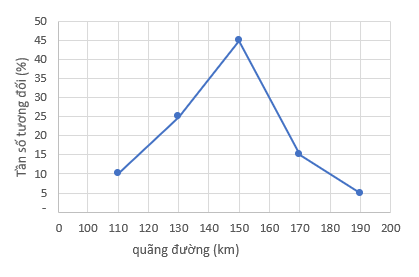
Biểu đồ dạng cột:

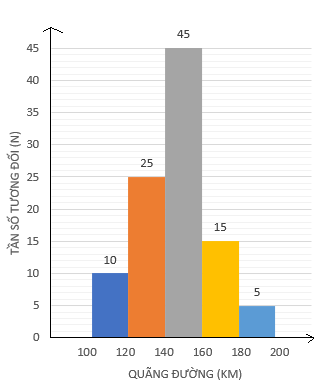
Giải rút gọn bài 6 trang 67 sgk toán 9 tập 2 cánh diều:

Mỗi nhân viên của một công ty làm biệc ở một trong năm bộ phận của công ty đó là: Hành chính – Nhân sự; Truyền thông – Quảng cáo; Kinh doanh; Sản xuất; Dịch vụ.

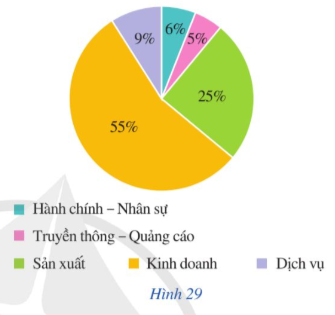Biểu đồ hình quạt tròn trong Hình 29 thống kê tỉ lệ nhân viên thuộc mỗi bộ phận.

Chọn ngẫu nhiên một nhân viên của công ty. Tính xác suất của mỗi biến cố sau:

A: “Nhân viên được chọn thuộc bộ phận Kinh doanh”;

B: “Nhân viên được chọn không thuộc bộ phân Hành chính – Nhân sự hay Dịch vụ”.

Lời giải rút gọn:

Kết quả thuận lợi cho biến cố A là: 55% tổng số nhân viên. Vậy xác suất cần tìm cho biến cố A là:

Kết quả thuận lợi cho biến cố B là: 55% + 25% + 5% = 75% tổng số nhân viên. => .

Giải rút gọn bài 7 trang 67 sgk toán 9 tập 2 cánh diều:

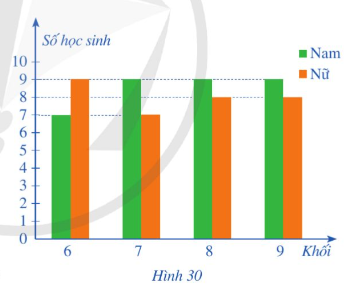
Biểu đồ cột kép ở Hình 30 biểu diễn số lượng học sinh tham gia giải thi đấu thể thao của một trường trung học cơ sơ.

Chọn ngẫu nhiên một học sinh tham gia giải thi đấu thể thao của trường đó. Tính xác suất của mỗi biến cố sau:

A: “Học sinh được chọn là nam”;

B: “Học sinh được chọn thuộc khối 6”;

C: “Học sinh được là nữ và không thuộc khối 9”.

Lời giải rút gọn:

Không gian mẫu trong bài này có tất cả 16 + 16 + 17 + 17 = 66 học sinh.

- Số kết quả thuận lợi cho biến cố A là: 7 + 9 + 9 + 9 = 43 học sinh

=>

- Số kết quả thuận lợi cho biến cố B là: 16 học sinh

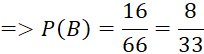
- Số kết quả thuận lợi cho biến cố C là: 9 + 7 + 8 = 24 học sinh

=> .

Giải rút gọn bài 8 trang 67 sgk toán 9 tập 2 cánh diều:

Trong một kì thi học sinh giỏi Toán, tỉ lệ học sinh đạt giải là 35%. Chọn ngẫu nhiên một học sinh đã tham gia kì thi đó. Tính xác suất của biến cố: “Học sinh được chọn đạt giải”.

Lời giải rút gọn:

Gọi số học sinh tham gia kì thi là x (x N^*; học sinh) 

Số kết quả thuận lợi cho biến cố là: 35%×x = 0,35x

=>