Slide bài giảng Toán 9 Cánh diều bài tập cuối chương V

Tóm lược nội dung

BÀI TẬP CUỐI CHƯƠNG V

Giải rút gọn bài 1 trang 124 sgk toán 9 tập 1 cánh diều

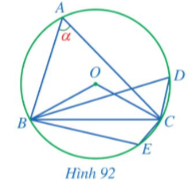
Trong Hình 92, cho các điểm A, B, C, D, E thuộc đường tròn (O)

Lời giải rút gọn:

a) Chọn B.

b) Chọn A.

c) Chọn C.

Giải rút gọn bài 2 trang 124 sgk toán 9 tập 1 cánh diều

a) Độ dài cung tròn có số đo 30^o của đường tròn bán kính R là

b) Diện tích hình quạt tròn tâm O, có bán kính R, cung có số đo 45^o là

Lời giải rút gọn:

a) Chọn D.

b) Chọn C.

Giải rút gọn bài 3 trang 124 sgk toán 9 tập 1 cánh diều

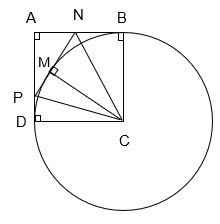
Cho hình vuông ABCD cạnh r và đường tròn (C; r). Giả sử M là một điểm nằm trên đường tròn (C; r) sao cho điểm M nằm trong hình vuông ABCD. Tiếp tuyến của đường tròn (C; r) tại tiếp điểm M cắt các đoạn thẳng AB, AD lần lượt tại N, P. Chứng minh:

a) Các đường thẳng NB, PD là các tiếp tuyến của đường tròn (C; r);

b) .

Lời giải rút gọn:

a) Xét đường tròn (C) có:

- NB BC tại B (giả thiết); B đường tròn (C)

NB là tiếp tuyến đường tròn (C).

- PD CD tại D (giả thiết); D đường tròn (C)

PD là tiếp tuyến đường tròn (C).

b) Xét đường tròn (O) có hai tiếp tuyến PD và PM cắt nhau tại P

CP là phân giác . (1)

Lại có hai tiếp tuyến MN và NB cắt nhau tại N

CN là phân giác . (2)

Ta có: . (3)

Từ (1), (2), (3)

(đpcm).

Giải rút gọn bài 4 trang 124 sgk toán 9 tập 1 cánh diều

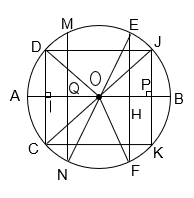
Chứng minh trong một đường tròn:

a) Đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy;

b) Đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy;

c) Hai dây bằng nhau thì cách đều tâm;

d) Hai dây cách đều tâm thì bằng nhau.

Lời giải rút gọn:

a) Ta có: OC = OD = R.

OCD cân tại O.

Mà OA CD tại I OI đồng thời là đường trung trực

I là trung điểm DC (đpcm).

b) Ta có: OE = OF = R.

OEF cân tại O.

Mà OEF có đường trung tuyến OH

OH đồng thời là đường cao của OEF (H AB) (đpcm).

c) Giả sử DC = JK; JK cắt AB tại P

Chứng minh tương tự câu a ta được P là trung điểm JK.

JP = PK = JK (1).

Vì I là trung điểm CD DI = IC = CD mà JK = CD (giả thiết) (2).

Từ (1) và (2) JP = PK = DI = IC.

Xét OID vuông tại I và OJP vuông tại P có:

OD = OJ = R

DI = JP (cmt)

OID = OJP (cạnh huyền – cạnh góc vuông)

OI = OP (hai cạnh tương ứng) (đpcm).

d) Giả sử dây MN cắt AB tại Q OQ là khoảng cách từ tâm đến AB.

Chứng minh tương tự câu a ta có Q là trung điểm MN.

MQ = QN = MN .

Xét OQN vuông tại Q và OHF vuông tại H có:

ON = OF = R

OQ = OH (gt)

OQN = OHF (cạnh huyền – cạnh góc vuông)

QN = HF (hai cạnh tương ứng).

MN = EF hay MN = EF (đpcm).

Giải rút gọn bài 5 trang 124 sgk toán 9 tập 1 cánh diều

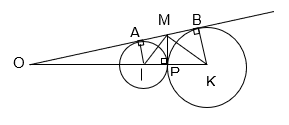
Cho hai đường tròn (I; r) và (K; R) tiếp xúc ngoài với nhau tại P với R r, đường thẳng a lần lượt tiếp xúc với (I; r) và  (K; R) tại A và B, a cắt KI tại O. Đường thẳng qua P vuông góc với IK cắt đường thẳng a tại M. Chứng minh:

a) ;              b) AB = 2MP;                  c) .

Lời giải rút gọn:

a) Xét OAI và OBK có:

chung

OAI đồng dạng với  OBK (g-g).

(tỷ số đồng dạng)

Hay (đpcm).

b) Xét đường tròn (I) có hai giao tuyến là MA và MP cắt nhau tại M; ( A, P (I))

MA = MP (1).

Xét đường tròn (K) có hai giao tuyến là MP và MB cắt nhau tại M; ( P, B (K))

MB = MP (2).

Từ (1) và (2) MA + MB = MP + MP hay 2MP = AB (đpcm).

c) Xét đường tròn (I) có hai giao tuyến là MA và MP cắt nhau tại M.

MI là phân giác = = .

Xét đường tròn (K) có hai giao tuyến là MB và MP cắt nhau tại M.

MK là phân giác = = .

Ta có: (đpcm).

Giải rút gọn bài 6 trang 125 sgk toán 9 tập 1 cánh diều

Mặt đĩa CD ở Hình 93 có dạng hình vành khuyên giới hạn bởi hai đường tròn cùng tâm và có bán kính lần lượt là 1,5 cm và 6 cm. Hình vành khuyên đó có diện tích bằng bao nhiêu centimét vuông (làm tròn kết quả đến hàng đơn vị)?

Lời giải rút gọn:

Diện tích đường tròn ngoài là:

(cm²)

Diện tích đường tròn trong là:

(cm²)

Diện tích vành khuyên là: 

(cm²).

Vậy diện tích vành khuyên là 106 cm².

Giải rút gọn bài 7 trang 125 sgk toán 9 tập 1 cánh diều

Hình 94 mô tả mảnh vải có dạng một phần tư hình vành khuyên, trong đó hình vành khuyên giới hạn bởi hai đường tròn cùng tâm và có bán kính lần lượt là 3 dm và 5 dm. Diện tích của mảnh vải đó bằng bao nhiêu decimét vuông (làm tròn kết quả đến hàng phần mười)?

Lời giải rút gọn:

Diện tích góc phần tư bên ngoài là:

(dm²)

Diện tích góc phần tư bên trong là:

(dm²)

Diện tích mảnh vải là: 

(dm²).

Giải rút gọn bài 8 trang 125 sgk toán 9 tập 1 cánh diều

Logo ở Hình 95 có dạng hình quạt tròn bán kính 8 cm và góc ở tâm bằng 60^o. Tính diện tích mỗi hình sau (theo đơn vị centimét vuông làm tròn kết quả đến hàng phần mười):

a) Toàn bộ logo;

b) Phần logo màu đỏ có dạng hình viên phân.

Lời giải rút gọn:

a) (cm²)

b) 

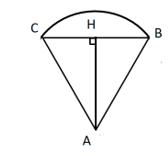
Kẻ AH BC (H BC)

ABC có ; AC = AB ABC đều.

AB = BC = AC = 8 cm (tính chất tam giác đều)

Mà ABC có đường cao AH AH đồng thời là đường trung tuyến của ABC.

HB = HC = BC = .8 = 4 (cm)

Ta có: (định lý Pytago)

(cm)

Diện tích tam giác ABC là: (cm²)

Diện tích phần màu đỏ là (cm²).

Giải rút gọn bài 9 trang 125 sgk toán 9 tập 1 cánh diều

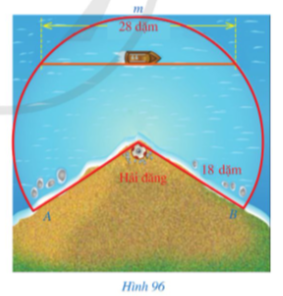
Hình 96 biểu diễn vùng mặt biển được chiếu sáng bởi một hải đăng có dạng hình quạt tròn với bán kính 18 dặm, cung AmB có số đo 245^o.

a) Hãy tính diện tích vùng mặt biển có thể nhìn thấy ánh sáng từ hải đăng theo đơn vị kilômét vuông (lấy 1 dặm = 1 609 m và làm tròn kết quả đến hàng đơn vị).

b) Giả sử một con thuyền di chuyển dọc theo dây cung có độ dài 28 dặm của đường tròn với tâm là tâm của hình quạt tròn, bán kính là 18 dặm. Tính khoảng cách nhỏ nhất từ con thuyền đến hải đăng (theo đơn vị dặm và làm tròn kết quả đến hàng đơn vị). 

Lời giải rút gọn:

Đổi 18 dặm = 28962 m = 28,962 km.

a) Ta có: số đo cung AB = 360^o – số đo cung AmB = 360^o – 245^o = 115^o.

Diện tích hình tròn là: (km²)

Diện tích phần chắn cung AB là: (km²)

Diện tích cần tìm là: (km²).

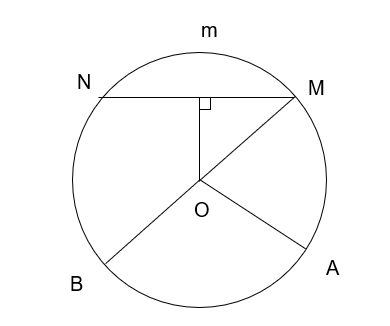
b) Gọi OH là khoảng cách từ ngọn hải đăng đến con thuyền

Để khoảng cách nhỏ nhất thì OH MN

Xét đường tròn (O) có dây cung  MN, OH MN

H là trung điểm MN

HN = HM = MN = .28 = 14 (dặm)

(pytago)

  (dặm).