Slide bài giảng Toán 9 Cánh diều bài 3: Giải hệ hai phương trình bậc nhất hai ẩn

Tóm lược nội dung

BÀI 3. GIẢI HỆ PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

Mở đầu: Một nhóm khách vào cửa hàng bán trà sữa. Nhóm khách đó đã mua 6 cốc trà sữa gồm trà sữa trân châu và trà sữa phô mai. Giá mỗi cốc trà sữa trân châu, trà sữa phô mai lần lượt là 33 000 đồng, 28 000 đồng. Tổng số tiền nhóm khách thanh toán cho cửa hàng là 188 000 đồng. Hỏi nhóm khách đó mua bao nhiêu cốc trà sữa mỗi loại?

Lời giải rút gọn:

Gọi x là số cốc trà sữa trân châu mà nhóm khách đã mua (x

Gọi y là số cốc trà sữa phô mai mà nhóm khách đã mua (y

Ta có:

Từ (1) ta có:

Thay vào (2) ta được:

x.33 000 + (6 – x). 28 000 = 188 000

Vậy nhóm khách đã mua 4 cốc trà sữa trân châu, 2 cốc trà sữa phô mai.

I. GIẢI HỆ PHƯƠNG TRÌNH BẰNG PHƯƠNG PHÁP THẾ

Hoạt động 1 trang 19 sgk toán 9 tập 1 cánh diều

Cho hệ phương trình (I)

Hãy giải hệ phương trình (I) theo các bước sau:

a) Từ phương trình (1), ta biểu diễn y theo x rồi thế vào phương trình (2) để được phương trình ẩn x.

b) Giải phương trình (ẩn x) vừa nhận được để tìm giá trị của x.

c) Thế giá trị vừa tìm được của x vào biểu thức biểu diễn y theo x ở câu a để tìm giá trị của y. Từ đó, kết luận nghiệm của hệ phương trình (I).

Lời giải rút gọn:

a) Từ phương trình (1) ta có

=> (3)

b) Giải phương trình (3)

Vậy x = 1

c) y = x + 3 = 1 + 3 = 4

Vậy x = 4

Vậy hệ phương trình đã cho có nghiệm (x ; y) = (1 ; 4).

Luyện tập, vận dụng 1 trang 20 sgk toán 9 tập 1 cánh diều

Giải hệ phương trình 

Lời giải rút gọn:

Từ (1) ta có x = 2 + 3y         (3)

=> –2(2 + 3y) + 5y = 1 (4)

Giải phương trình (4):

• x =

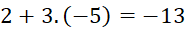
Vậy hệ phương trình đã cho có nghiệm (x ; y) = (.

Luyện tập, vận dụng 2 trang 20 sgk toán 9 tập 1 cánh diều

Lời giải rút gọn:

Từ phương trình (2), ta có:

=>            (4)

Giải phương trình (4):

• Phương trình (4) vô nghiệm. Vậy hệ phương trình đã cho vô nghiệm.

Luyện tập, vận dụng 3 trang 21 sgk toán 9 tập 1 cánh diều

Lời giải rút gọn:

Từ phương trình (1) ta có: x = 4 + 3y                 (3)

=>               (4)

Giải phương trình (4):               

0y =0

• Phương trình (4) có vô số nghiệm. Vậy hệ phương trình đã cho có vô số nghiệm.

II. GIẢI HỆ PHƯƠNG TRÌNH BẰNG PHƯƠNG PHÁP CỘNG ĐẠI SỐ

Hoạt động 2 trang 21 sgk toán 9 tập 1 cánh diều

Cho hệ phương trình     (II)

a) Các hệ số của y trong hai phương trình (1) và (2) có đặc điểm gì?

b) Cộng từng vế hai phương trình của hệ (II), ta nhận được phương trình nào?

c) Giải phương trình nhận được ở câu b. Từ đó, ta tìm được nghiệm của hệ phương trình (II).

Lời giải rút gọn:

a) Đối nhau.

b) 2x = 8

c) Ta có 2x = 8 => x = 4

Thế x = 4 vào phương trình (1) => 4 + y = 7   

• y = 3.

Vậy hệ phương trình đã cho có nghiệm (x ; y) = (4 ; 3).

Luyện tập, vận dụng 4 trang 21 sgk toán 9 tập 1 cánh diều

Giải hệ phương trình

Lời giải rút gọn:

Trừ từng vế hai phương trình (2) và (1) => 2x = 2 => x = 1.

Thế x = 1 vào phương trình (1): 3.1 + 2.y = 5   (3)

=> 3.1 + 2.y = 5

=> y = 1.

Vậy hệ phương trình đã cho có hai nghiệm (x ; y) = (1 ; 1).

Hoạt động 3 trang 22 sgk toán 9 tập 1 cánh diều

Cho hệ phương trình

a) Các hệ số của x trong hai phương trình (1) và (2) có bằng nhau (hoặc đối nhau) hay không? Các hệ số của y trong hai phương trình (1) và (2) có bằng nhau (hoặc đối nhau) hay không?

b) Nhân hai vế của phương trình (1) với 3 và nhân hai vế của phương trình (2) với 2, ta được hệ phương trình mới với hệ số của x trong hai phương trình đó có đặc điểm gì?

c) Giải hệ phương trình nhận được ở câu b. Từ đó, ta được nghiệm của hệ phương trình (III).

Lời giải rút gọn:

a) x: Đối nhau

y: không đối nhau hoặc bằng nhau.

b) 

Hệ số x trong hai phương trình đối nhau.

c) Cộng từng vế hai phương trình (3) và (4), ta nhận được phương trình: 

29y = (5)

=>y =

Thế giá trị y = vào phương trình (1):

2x + 5(=                 (6)

=>2x + 5(=                 

=>x =1.

Vậy hệ phương trình đã cho có nghiệm (x ; y) = (1 ; -1).

Luyện tập, vận dụng 5 trang 23 sgk toán 9 tập 1 cánh diều

Giải bài toán ở phần mở đầu.

Lời giải rút gọn:

Gọi x là số cốc trà sữa trân châu mà nhóm khách đã mua (x

Gọi y là số cốc trà sữa phô mai mà nhóm khách đã mua (y

Ta có:

Từ (1) ta có:

Thay vào (2) ta được:

x.33 000 + (6 – x). 28 000 = 188 000

Vậy nhóm khách đã mua 4 cốc trà sữa trân châu, 2 cốc trà sữa phô mai.

III. SỬ DỤNG MÁY TÍNH CẦM TAY ĐỂ TÌM NGHIỆM CỦA HỆ HAI PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

Luyện tập, vận dụng 6 trang 24 sgk toán 9 tập 1 cánh diều.

Sử dụng máy tính cầm tay để tìm nghiệm của hệ phương trình

Lời giải rút gọn:

Sử dụng máy tính cầm tay ta thấy trên màn hình hiện ra x =

IV. GIẢI BÀI TẬP CUỐI SÁCH

Giải chi tiết bài 1 trang 25 sgk toán 9 tập 1 cánh diều

Giải các hệ phương trình sau bằng phương pháp thế:

b)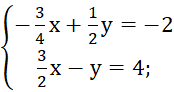

Lời giải rút gọn:

Từ phương trình thứ (1), ta có x = 2y       

Thế vào (2), ta được: 3.(2y) + 2y = 8         (3)

=>6y + 2y = 8

=>y = 1

Mà x = 2y nên x = 2.1 = 2

Vậy nghiệm của hệ phương trình là (x ; y) = (2 ; 1).

b)

Từ phương trình (2), ta có: y =

Thay vào phương trình (1), ta được:        (3)

• 
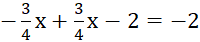
• 0x = 0

Vậy phương trình (3) có vô số nghiệm

Vậy hệ có vô số nghiệm.

Từ phương trình (2), ta có: y = 2x

Thế vào phương trình (1), ta được: 4x – 2.2x = 1  (3)

=> 4x – 4x = 1

=> 0x = 1

Vậy phương trình (3) vô nghiệm

Vậy hệ phương trình đã cho vô nghiệm.

Giải chi tiết bài 2 trang 25 sgk toán 9 tập 1 cánh diều

Giải các hệ phương trình sau bằng phương pháp cộng đại số:

a)

b)

c)

d)

Lời giải rút gọn:

a)

Cộng từng vế phương trình (1) với phương trình (2) ta được: 3x = 6 (3)

Giải phương trình (3), ta được x =2

Thay x = 2 vào phương trình (2) => y = 0

Vậy hệ phương trình có nghiệm (x ; y) = (2 ; 0).

b)

=>

Trừ từng vế phương trình (3) cho phương trình (4) ta được: 11y = 11 (5)

• y = 1

Thay y = 1 vào (1) ta được:

• x =

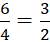
Vậy nghiệm của hệ phương trình đã cho (x ; y) =

c)

=>

Cộng từng vế hai phương trình (3) và (4), ta được: 0x + 0y = 0 (5)

Vậy phương trình (5) có vô số nghiệm

Vậy hệ phương trình đã cho có vô số nghiệm.

d)

=>

Cộng từng vế hai phương trình của hệ mới, ta được 0x + 0y = 10 (5)

Vậy phương trình (5) vô nghiệm

Vậy hệ phương trình đã cho vô nghiệm.

Giải chi tiết bài 3 trang 25 sgk toán 9 tập 1 cánh diều

Xác định a, b để đồ thị của hàm số y = ax +b đi qua hai điểm A, B trong mỗi trường hợp sau: 

a) A(1 ; – 2) và B(– 2 ; – 11); 

b) A(2 ; 8) và B (– 4 ; 5).

Lời giải rút gọn:

a) Đồ thị hàm số y = ax + b đi qua điểm A(1 ; – 2): – 2 = a.1 + b

Hay a + b = – 2 (1)

Đồ thị hàm số y = ax + b đi qua điểm B(– 2 ; – 11): – 11 = a.(– 2) + b

Hay – 2a + b = – 11 (2)

Vậy a, b chính là nghiệm của hệ phương trình (1) và (2)

Trừ từng vế của phương trình (1) cho (2), ta được 3a = 9

a = 3

=>b = – 5

Vậy đồ thị hàm số có dạng: y = 3x – 5. 

b) Đồ thị hàm số y = ax + b đi qua điểm A(2 ; 8): 8 = a.2 + b

Hay 2a + b = 8 (1)

Đồ thị hàm số y = ax + b đi qua điểm B(– 4 ; 5): 5 = a.(– 4) + b

Hay – 4a + b = 5 (2)

Vậy a, b chính là nghiệm của hệ phương trình (1) và (2)

Trừ từng vế của phương trình (1) cho (2), ta được 6a = 3

a =

=>b = 7

Vậy đồ thị hàm số có dạng: y = . 

Giải chi tiết bài 4 trang 25 sgk toán 9 tập 1 cánh diều

Một ca nô đi xuôi dòng một quãng đường 42 km hết 1 giờ 30 phút và ngược dòng quãng đường đó hết 2 giờ 6 phút. Tính tốc độ của ca nô khi nước yên lặng và tốc độ của dòng nước. Biết rằng tốc độ của ca nô khi nước yên lặng không đổi trên suốt quãng đường và tốc độ của dòng nước cũng không đổi khi ca nô chuyển động.

Lời giải rút gọn:

Gọi x là vận tốc của ca nô khi nước yên lặng 

Gọi y là vận tốc của dòng nước (x, y > 0)

1 giờ 30 phút = giờ

2 giờ 6 phút =

Ca nô đi xuôi dòng thì vận tốc là: x + y (km/h)

Ca nô đi ngược dòng thì vận tốc là: x – y (km/h)

Có:           

Hay x + y = 28    (1)

Ca nô đi ngược dòng quãng đường đó hết 2 giờ 6 phút nên ta có phương trình:

Hay x – y = 20     (2)

Nên x, y là nghiệm của hệ (1) và (2):

Giải hệ phương trình, ta cộng từng vế hai phương trình của hệ, ta được: 2x = 48

x = 24

=>y = 4

Vậy vận tốc của ca nô là 24 km/h và vận tốc của dòng nước là 4 km/h.

Giải chi tiết bài 5 trang 25 sgk toán 9 tập 1 cánh diều

Bác Phương chia số tiền 800 triệu đồng của mình cho hai khoản đầu tư. Sau một năm, tổng số tiền lãi thu được là 54 triệu đồng. Lãi suất cho khoản đầu tư thứ nhất là 6%/năm và khoản đầu tư thứ hai 8%/năm. Tính số tiền bác Phương đầu tư cho mỗi khoản.

Lời giải rút gọn:

Gọi x (triệu đồng) là số tiền bác Phương đầu tư cho khoản thứ nhất

Gọi y (triệu đồng) là số tiền bác Phương đầu tư cho khoản thứ hai

(0 < x, y < 800)

x + y = 800    (1)

Lãi suất cho khoản đầu tư thứ nhất là 6%/năm, số tiền là:

6%.x = 0,06x

Lãi suất cho khoản đầu tư thứ hai là 8%/năm, số tiền là:

8%.y = 0,08y

Tổng số tiền lãi thu được là 54 triệu đồng, nên ta có phương trình:

0,06x + 0,08y = 54

Hay 6x + 8y = 5400            (2)

Từ (1) và (2) ta có hệ phương trình:

=>

Trừ phương trình (4) cho phương trình (3) ta được: y = 300

=>x = 500

Vậy số tiền bác Phương đầu tư cho khoản thứ nhất là 500 triệu đồng, khoản thứ hai là 300 triệu đồng.

Giải chi tiết bài 6 trang 25 sgk toán 9 tập 1 cánh diều

Nhân dịp ngày Giỗ Tổ Hùng Vương, một siêu thị điện máy đã giảm giá nhiều mặt hàng để kích cầu mua sắm. Giá niêm yết của mottj chiếc tủ lạnh và một chiếc máy giặt có tổng số tiền là 25,4 triệu đồng. Tuy nhiên, trong dịp này tủ lạnh giảm 40% giá niêm yết và máy giặt giảm 25% giá niêm yết. Vì thế, cô Liên đã mua hai mặt hàng trên với tổng số tiền là 16,77 triệu đồng. Hỏi giá niêm yết của mỗi mặt hàng trên là bao nhiêu?

Lời giải rút gọn:

Gọi x, y (triệu đồng) lần lượt là giá niêm yết cua tủ lạnh và máy giặt 

(0 < x, y < 25,4)

x + y = 25,4    (1)

Giá của tủ lạnh sau khi được giảm giá là: x – 40%.x = x – 0,4x = 0,6x

Giá của máy giặt sau khi được giảm giá là: y – 25%.y = y – 0,25y = 0,75y

0,6x + 0,75y = 16,77    (2)

Từ (1) và (2) ta có hệ phương trình: 

=>

Trừ từng vế phương trình thứ (4) cho phương trình thứ (3): 0,15y = 1,53

y = 10,2 (thỏa mãn điều kiện)

=>x = 15,2 (thỏa mãn điều kiện)

Vậy giá niêm yết lúc đầu của tủ lạnh là 15,2 triệu đồng và của máy giặt là 10,2 triệu đồng.

Giải chi tiết bài 7 trang 25 sgk toán 9 tập 1 cánh diều

Tìm các hệ số x, y để cân bằng mỗi phương trình phản ứng hóa học sau:

a) 2Fe + yCl₂  xFeCl₃;

b) xFeCl₃ + Fe ₂

Lời giải rút gọn:

a) 2Fe + yCl₂  xFeCl₃;

Ta có: Số nguyên tử Fe: 2 = x              (1)

Số nguyên tử Cl: 2y = 3x                     (2)

Thay x = 2 từ phương trình (1) vào phương trình (2) => y = 3

=> 2Fe + 3Cl₂  2FeCl₃

b) xFeCl₃ + Fe ₂

Ta có: Số nguyên tử Fe: x + 1 = y        (1)

Số nguyên tử Cl: 3x = 2y                     (2)

=>3x = 2(x + 1) 

Thay x = 2 vào phương trình (1) ta được: y = 3

• 2FeCl₃ + Fe ₂