Slide bài giảng Toán 9 Cánh diều bài 2: Bất phương trình bậc nhất một ẩn

Tóm lược nội dung

BÀI 2. BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN

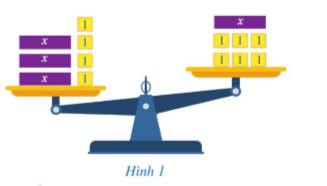
Mở đầu: Giả sử mỗi hộp màu tím đặt trên đĩa cân ở Hình 1 đều có khối lượng là x kg, còn mỗi hộp màu vàng đều có khối lượn là 1kg. Khi đó, hai biểu thức biểu thị (theo x) tổng khối lượng các hộp xếp ở đĩa cân bên trái, đĩa cân bên phải lần lượt là 3x + 4, x + 6. Do đĩa cân lệch về bên trái nên ta có hệ thức: 

3x + 4 > x + 6. Trong toán học, hệ thức 3x + 4 > x + 6 được gọi là gì?

Lời giải rút gọn:

Là bất phương trình bậc nhất một ẩn.

I. MỞ ĐẦU VỀ BẤT PHƯƠNG TRÌNH MỘT ẨN

Hoạt động 1 trang 35 sgk toán 9 tập 1 cánh diều

Xét hệ thức 3x + 4 > x + 6 (1) nêu trong bài toán ở phần mở đầu.

a) Các biểu thức 3x + 4, x + 6 có phải là hai biểu thức của cùng một biến x hay không?

b) Khi thay giá trị x = 5 vào hệ thức (1), ta có được một khẳng định đúng hay không?

Lời giải rút gọn:

a) Là hai biểu thức cùng một biến x 

b) Thay x = 5

=>3x + 4 = 3.5 + 4 = 19

x + 6 = 5 + 6 = 11

Mà 19 > 11

Khẳng định đúng.

Luyện tập, vận dụng 1 trang 36 sgk toán 9 tập 1 cánh diều

Cho biết giá trị x = 3 là nghiệm của bất phương trình nào trong các bất phương trình sau:

a) 5x + 4 > 5x – 12;

b)

Lời giải rút gọn:

a) 5.3 + 4 > 5.3 – 12  là khẳng định đúng. Vậy x = 1 là nghiệm của bất phương trình đã cho.

b) là khẳng định không đúng. Vậy x = 3 không là nghiệm của bất phương trình đã cho.

II. BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN

Hoạt động 2 trang 36 sgk toán 9 tập 1 cánh diều

Cho bất phương trình (ẩn x): 5x + 20 > 0.

Đa thức ở vế trái của phương trình đó có bậc bằng bao nhiêu?

Lời giải rút gọn:

Bậc bằng 1.

Luyện tập, vận dụng 2 trang 36 sgk toán 9 tập 1 cánh diều

Nêu hai ví dụ về bất phương trình bậc nhất ẩn x

Lời giải rút gọn:

a) 2x + 5

b) 4x – 7

Luyện tập, vận dụng 3 trang 37 sgk toán 9 tập 1 cánh diều

Kiểm tra xem x = – 7 có phải là nghiệm của bất phương trình bậc nhất 

hay không? 

Lời giải rút gọn:

Thay x = – 7, ta có là  khẳng định đúng. Vậy x = – 7 là nghiệm của bất phương trình

Hoạt động 3 trang 37 sgk toán 9 tập 1 cánh diều

Giải bất phương trình: 4x – 32 < 0                 (2)

Lời giải rút gọn:

4x – 32 < 0

ó4x < 32

óx < 8.

Vậy nghiệm của bất phương trình (2) là x < 8.

Luyện tập, vận dụng 4 trang 38 sgk toán 9 tập 1 cánh diều

Giải các bất phương trình: 

a)

b)

Lời giải rút gọn:

a)

b)

Hoạt động 4 trang 38 sgk toán 9 tập 1 cánh diều

Giải bất phương trình: 3x + 4 > x + 12

Lời giải rút gọn:

3x + 4 > x + 12

ó3x + 4 – x > 12 

ó2x > 8

óx > 4.

Luyện tập, vận dụng 5 trang 38 sgk toán 9 tập 1 cánh diều

Giải bất phương trình:

2(x – 0,5) – 1,4 1,5 – (x + 1,2) 

Lời giải rút gọn:

2(x – 0,5) – 1,4 1,5 – (x + 1,2) 

III. GIẢI BÀI TẬP CUỐI SGK 

Giải chi tiết bài 1 trang 40 sgk toán 9 tập 1 cánh diều

Kiểm tra xem số nào là nghiệm của mỗi bất phương trình tương ứng sau đây:

a)

b)

Lời giải rút gọn:

a) Thay x = – 3, ta có: là khẳng định đúng. 

Vậy x = – 3 là nghiệm của bất phương trình  

Thay x = 1,5, ta có: là khẳng định không đúng.

Vậy x = 1,5 không là nghiệm của bất phương trình

b) Thay x = , ta có: là khẳng định đúng.

Vậy x = là nghiệm của bất phương trình 2 – 2x < 3x + 1.

Thay x = , ta có: là khẳng định không đúng.

Vậy x = không là nghiệm của bất phương trình 2 – 2x < 3x + 1.

Giải chi tiết bài 2 trang 40 sgk toán 9 tập 1 cánh diều

Giải các bất phương trình:

a) 2x + 6 > 1; 

b) 0,6x + 2 > 6x + 9;

c) 1,7x + .

Lời giải rút gọn:

a) 2x + 6 > 1

b)

c) 1,7x +

Giải chi tiết bài 3 trang 41 sgk toán 9 tập 1 cánh diều

Giải các bất phương trình:

a)

b)

c)

Lời giải rút gọn:

a)

8 – 3x – 2x < 10 

– 5x < 2 

b)

9 – 6x – (6 + 4x) > 0

9 – 6x – 6 – 4x > 0

10x < 3

x <

c)

4,2x + 4x – 8 – x > 6

7,2x > 14

x >

Giải chi tiết bài 4 trang 41 sgk toán 9 tập 1 cánh diều

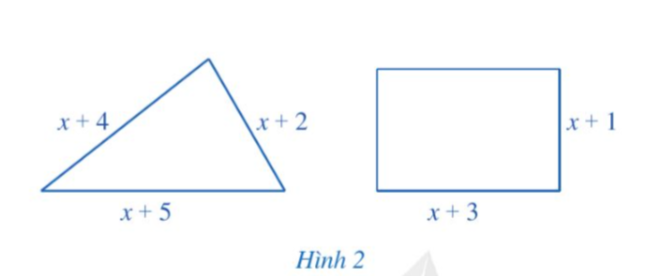
Tìm số thực dương x sao cho ở Hình 2 chu vi của tam giác lớn hơn chu vi của hình chữ nhật:

Lời giải rút gọn:

Chu vi hình tam giác: x + 4 + x + 2 + x + 5 = 3x + 11

Chu vi hình chữ nhật: [(x + 3) + (x + 1)].2 = (x + 3 + x + 1).2 

= (2x + 4).2 = 4x + 8

Chu vi hình tam giác lớn hơn chu vi hình chữ nhật ta có:

3x + 11 > 4x + 8

x < 3

Vậy 0 < x < 3 là số thực dương cần tìm.

Giải chi tiết bài 5 trang 41 sgk toán 9 tập 1 cánh diều

Một kho chứa 100 tấn xi măng, mỗi ngày đều xuất đi 20 tấn xi măng. Gọi x là số ngày xuất xi măng của kho đó. Tìm x sao cho sau x ngày xuất hàng, khối lượng xi măng còn lại trong kho ít nhất là 10 tấn.

Lời giải rút gọn:

Số xi măng xuất sau x ngày là: 20x (tấn)  (x > 0)

Số xi măng còn lại sau x ngày: 100 – 20x (tấn)

Để khối lượng xi măng còn lại trong kho ít nhất là 10 tấn ta có:

100 – 20x

Vậy sau 4 ngày xuất hàng, khối lượng xi măng còn lại trong kho còn lại ít nhất là 10 tấn.