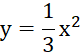Slide bài giảng Toán 9 Cánh diều bài 1: Hàm số y = ax^2 (a ≠ 0)
Slide điện tử bài 1: Hàm số y = ax^2 (a ≠ 0). Kiến thức bài học được hình ảnh hóa, sinh động hóa. Trình bày với các hiệu ứng hiện đại, hấp dẫn. Giúp học sinh hứng thú học bài. Học nhanh, nhớ lâu. Có tài liệu này, hiệu quả học tập của học môn Toán 9 Cánh diều sẽ khác biệt
Bạn chưa đủ điều kiện để xem được slide bài này. => Xem slide bài mẫu
Tóm lược nội dung
BÀI 1. HÀM SỐ Y = AX2 (A 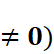
Mở đầu: Hàm số y = ![]() và đồ thị của hàm số đó có những tính chất như thế nào?
và đồ thị của hàm số đó có những tính chất như thế nào?
Tính chất: 5 ![]()
I. HÀM SỐ 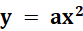 (A
(A 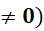
Hoạt động 1 trang 46 sgk toán 9 tập 2 cánh diều
Xét hàm số y = ![]() trong tình huống ở phần mở đầu.
trong tình huống ở phần mở đầu.
Hàm số đó có dạng y = ![]() (a
(a ![]() hay không? Nếu có, hãy xác định hệ số a của
hay không? Nếu có, hãy xác định hệ số a của ![]() .
.
Lời giải rút gọn:
Hàm số đó có dạng y = ![]() (a
(a ![]() .
.
Hệ số a là 5.
Luyện tập, vận dụng 1 trang 47 sgk toán 9 tập 2 cánh diều
Hàm số nào sau đây có dạng y = ![]() (a
(a![]() Đối với những hàm số đó, xác định hệ số a của
Đối với những hàm số đó, xác định hệ số a của ![]() .
.
a) ![]()
b) ![]() .
.
c) ![]()
Lời giải rút gọn:
a) -1.
b) ![]()
Luyện tập, vận dụng 2 trang 47 sgk toán 9 tập 2 cánh diều
Cho hàm số y = ![]() Tính giá trị của y khi:
Tính giá trị của y khi:
a) x = -3;
b) x = 0;
c) x = 3.
Lời giải rút gọn:
a) y = ![]()
b) y = ![]()
c) y = ![]()
II. ĐỒ THỊ CỦA HÀM SỐ 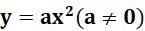
Hoạt động 2 trang 47 sgk toán 9 tập 2 cánh diều
a) Nêu khái niệm đồ thị của hàm số y = f(x).
b) Xét hàm số y = ![]() Hãy thực hiện các hoạt động sau:
Hãy thực hiện các hoạt động sau:
- Tìm giá trị của y tương ứng với giá trị của x trong bảng sau:

- Trên mặt phẳng tọa độ Oxy, xác định các điểm có hoành độ và tung độ nhưng trong bảng giá trị trên.
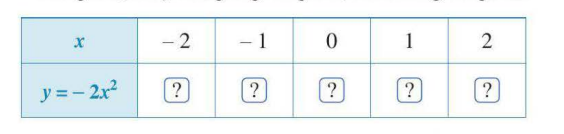
- Quan sát Hình 1, vẽ đường cong như ở Hình 1 đi qua 5 điểm A, B, O, C, D. Đường cong đó được gọi là đường parabol và đường parabol đó là đồ thị của hàm số y = ![]()
c) Xét hàm số y =![]() Hãy thực hiện các hoạt động sau:
Hãy thực hiện các hoạt động sau:
- Tìm giá trị của y tương ứng với giá trị của x trong bảng sau:
- Tên mặt phẳng tọa độ Oxy, xác định các điểm có hoành độ và tung độ như trong bảng giá trị trên.
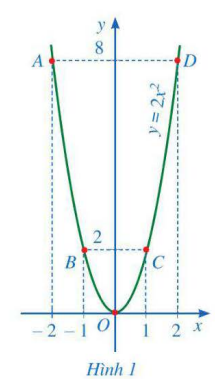
- Quan sát Hình 2, vẽ đường cong như ở Hình 2 đi qua 5 điểm M, N, O, P, Q. Đường cong đó được gọi là đường parabol và đường parabol đó là đồ thị của hàm số y = ![]()
Lời giải rút gọn:
a) Với mỗi giá trị x sẽ tương ứng với 1 giá trị y.
b)
| x | -2 | -1 | 0 | 1 | 2 |
8 | 2 | 0 | 2 | 8 |
Điểm (-2; 8)
Điểm (-1; 2)
Điểm (0; 0)
Điểm (1;2)
Điểm (2;8)
c)
| x | -2 | -1 | 0 | 1 | 2 |
-8 | -2 | 0 | -2 | -8 |
Điểm (-2; -8)
Điểm (-1; -2)
Điểm (0; 0)
Điểm (1; -2)
Điểm (2; -8)
Luyện tập, vận dụng 3 trang 49 sgk toán 9 tập 2 cánh diều
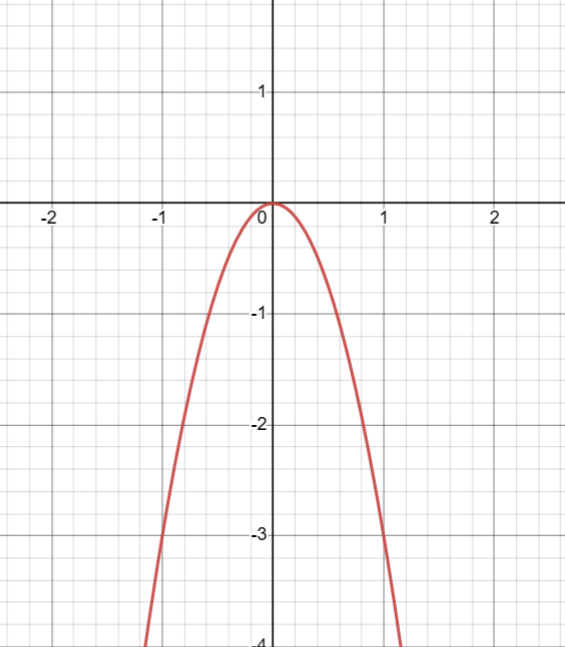
Vẽ đồ thị của hàm số ![]()
Lời giải rút gọn:
III. GIẢI BÀI TẬP CUỐI SGK
Giải rút gọn bài 1 trang 51 sgk toán 9 tập 2 cánh diều
Cho hàm số y = ![]() Tìm a, biết rằng khi x = -3 thì y = 5.
Tìm a, biết rằng khi x = -3 thì y = 5.
Lời giải rút gọn:
Thay x = -3 và y = 5
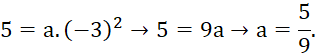
Giải rút gọn bài 2 trang 51 sgk toán 9 tập 2 cánh diều
Cho hàm số y = ![]()
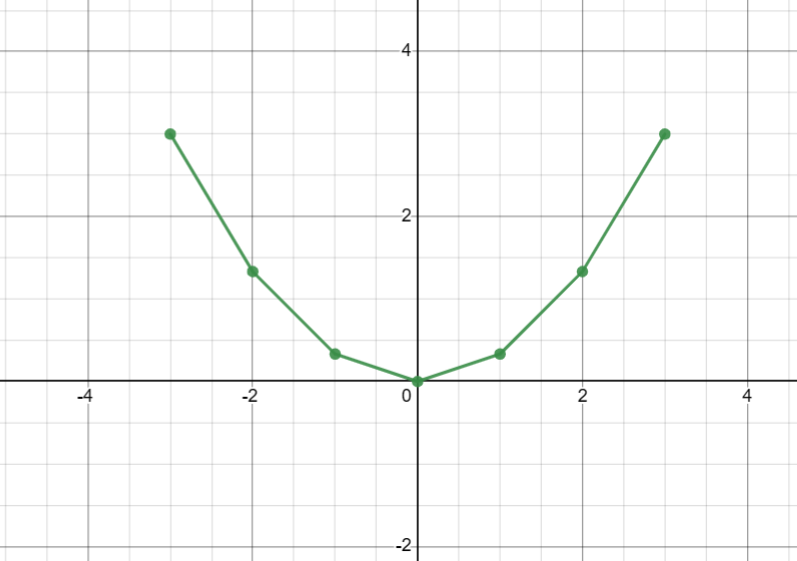
a) Tìm giá trị của y tương ứng với giá trị của x trong bảng sau:

b) Dựa vào bảng giá trị trên, vẽ đồ thị của hàm số đó.
c) Tìm những điểm thuộc đồ thị của hàm số có hoành độ lần lượt bằng -6; 10.
d) Tìm những điểm thuộc đồ thị của hàm số có tung độ bằng 27.
Lời giải rút gọn:
a)
x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| 3 |
|
| 0 |
|
| 3 |
b)
c) Khi y = 12 hoặc ![]()
d) Tung độ bằng 27
27 = ![]()
Giải rút gọn bài 3 trang 51 sgk toán 9 tập 2 cánh diều
Trên mặt phẳng tọa độ Oxy, điểm M(2; -1) thuộc đồ thị của hàm số y = ![]()
a) Tìm hệ số a.
b) Điểm A (4; -4) có thuộc đồ thị của hàm số hay không?
c) Hãy tìm một số điểm (không kể điểm O) thuộc đồ thị của hàm số, rồi vẽ đồ thị của hàm số.
Lời giải rút gọn:
a) Với x = 2; y = -1
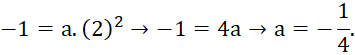
b) Thay x = 4; a = ![]()
Điểm A (4; -4) thuộc đồ thị của hàm số.
c) Hàm số y = ![]()
x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
y = | -4 |
| -1 |
| 0 |
| -1 |
| -4 |
Vẽ đồ thị hàm số
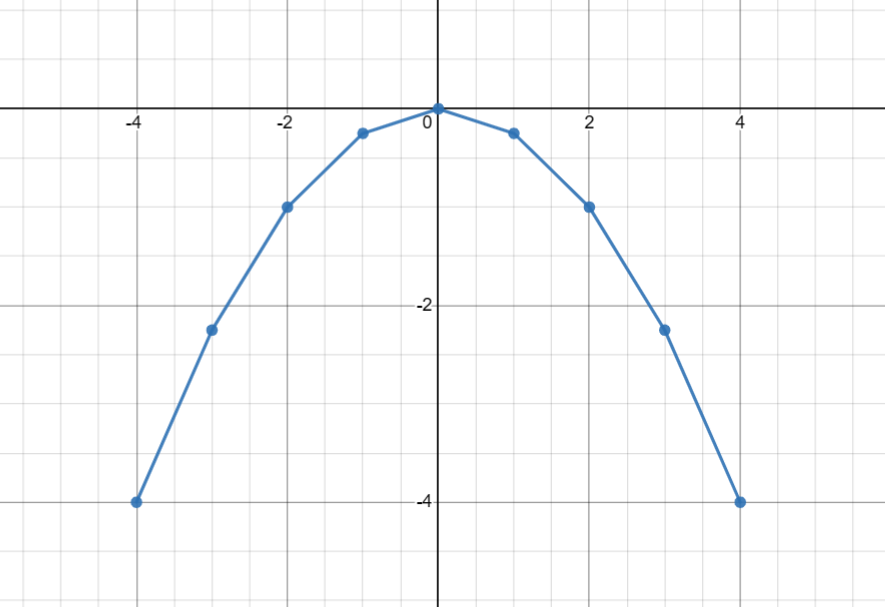
Điểm (-2; -4) không thuộc đồ thị hàm số.
Giải rút gọn bài 4 trang 51 sgk toán 9 tập 2 cánh diều
Hàm số y = ![]() biểu thị quãng đường (đơn vị: mét) mà một chiếc xe đua đi được trong khoảng thời gian t (giây). Giả sử một chiếc xe đua đi được 125 m sau khoảng thời gian là 5 giây.
biểu thị quãng đường (đơn vị: mét) mà một chiếc xe đua đi được trong khoảng thời gian t (giây). Giả sử một chiếc xe đua đi được 125 m sau khoảng thời gian là 5 giây.
a) Tìm hệ số a.
b) Vẽ đồ thị của hàm số đó.
Lời giải rút gọn:
a) Thay t = 5 và y = 125
![]()
y = ![]()
b) Vẽ đồ thị của hàm số đó
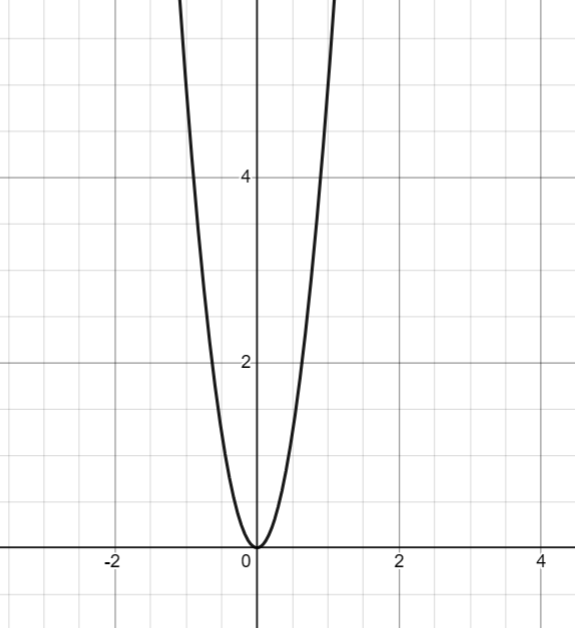
Giải rút gọn bài 5 trang 51 sgk toán 9 tập 2 cánh diều
Cá heo có thể nhảy cao tới 25 feet và thực hiện các thủ thuật như nhảy qua vòng, lộn nhào trong không trung. Giả sử quỹ đạo nhảy của cá heo là parabol ![]() , với gốc tọa độ là vị trí cao nhất mà cá heo đạt được, cách mặt nước 25 feet, trong đó y được tính theo đơn vị feet và x được tính theo đơn vị giây (Hình 6). Biết rằng sau 2 giây kể từ vị trí cao nhất đó, cá heo rơi chạm mặt nước. Tìm hàm số biểu thị quỹ đạo nhảy của cá heo.
, với gốc tọa độ là vị trí cao nhất mà cá heo đạt được, cách mặt nước 25 feet, trong đó y được tính theo đơn vị feet và x được tính theo đơn vị giây (Hình 6). Biết rằng sau 2 giây kể từ vị trí cao nhất đó, cá heo rơi chạm mặt nước. Tìm hàm số biểu thị quỹ đạo nhảy của cá heo.
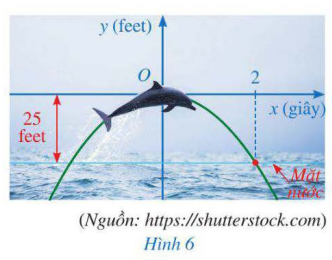
Lời giải rút gọn:
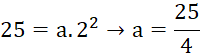
Hàm số biểu thị quỹ đạo nhảy của cá heo: ![]() .
.