Slide bài giảng Toán 9 Cánh diều bài 2: Một số hệ thức về cạnh và góc trong tam giác vuông

Tóm lược nội dung

BÀI 4. MỘT SỐ HỆ THỨC VỀ CẠNH VÀ GÓC TRONG TAM GIÁC VUÔNG

Mở đầu: Hình 12 mô tả đường lên dốc ở Hình 11, trong đó góc giữa BC và phương nằm ngang BA là = 15. Cạnh góc vuông AC và cạnh huyền BC (Hình 12) có liên hệ với nhau như thế nào?

Lời giải rút gọn:

Mối liên hệ: sin

Hay AC = BC. sin 15.

I. TÍNH CẠNH GÓC VUÔNG THEO CẠNH HUYỀN VÀ TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN

Hoạt động 1 trang 82 sgk toán 9 tập 1 cánh diều

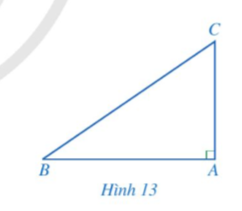
Cho tam giác ABC vuông tại A (Hình 13).

a) Biểu diễn sin B, cos C theo AC, BC.

b) Viết công thức tính AC theo BC và sin B.

c) Viết công thức tính AC theo BC và cos C.

Lời giải rút gọn:

a) sin B =

b) AC = BC.sin B

c) AC = BC.cos C

Luyện tập, vận dụng 1 trang 83 sgk toán 9 tập 1 cánh diều

Tính độ cao AC trong hình 12 khi BC = 20 m (làm tòn kết quả đếnh hàng phần mười của mét).

Lời giải rút gọn:

sin 15

AC = BC.sin 15 = 20. sin 15

Luyện tập, vận dụng 2 trang 83 sgk toán 9 tập 1 cánh diều

Cho tam giác nhọn ABC có đường cao CK. Biểu diễn CK theo AC và sin A. Từ đó, chứng minh diện tích của tam giác ABC bằng

Lời giải rút gọn:

Diện tích tam giác ABC là                         

sin =

Ta có:

Vậy diện tích của tam giác ABC bằng

II. TÍNH CẠNH GÓC VUÔNG THEO CẠNH GÓC VUÔNG CÒN LẠI VÀ TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN

Hoạt động 2 trang 84 sgk toán 9 tập 1 cánh diều

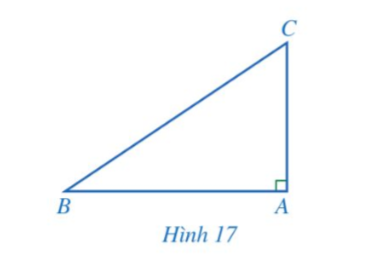
Cho tam giác ABC vuông tại A (Hình 17).

a) Biểu diễn tan B, cot C theo AB, AC.

b) Viết công thức tính AC theo AB và tan B.

c) Viết công thức tính AC theo AB và cot C.

Lời giải rút gọn:

a) tan

cot

b)

c) .

Hoạt động 3 trang 84 sgk toán 9 tập 1 cánh diều

Tính độ dài cạnh AB trong Hình 17 khi AC = 4 cm và = 34 (làm tròn kết quả đến hàng phần mười của centimét).

Lời giải rút gọn:

Ta có: tan

AB = .

III. ÁP DỤNG TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN ĐỂ GIẢI TAM GIÁC VUÔNG

Luyện tập, vận dụng 4 trang 85 sgk toán 9 tập 1 cánh diều

Tìm độ dài cạnh góc vuông AC và số đo các góc nhọn B, C của tam giác vuông ABC, biết cạnh góc vuông AB = 5 cm và cạnh góc vuông BC = 13 cm.

Lời giải rút gọn:

(cm)

Ta có: tan

Luyện tập, vận dụng 5 trang 85 sgk toán 9 tập 1 cánh diều

Tìm số đo góc nhọn C và độ dài cạnh góc vuông AB, cạnh huyền BC của tam giác vuông ABC, biết cạnh góc vuông AC = 7 cm và

Lời giải rút gọn:

tan

AB (cm)

BC = .

Luyện tập, vận dụng 6 trang 86 sgk toán 9 tập 1 cánh diều

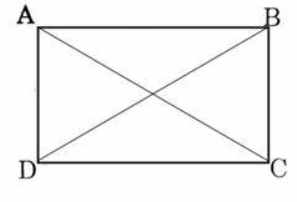
Cho hình chữ nhật ABCD thỏa mãn AC = 6 cm, = 47. Tính độ dài các đoạn thẳng AB, AD.

Lời giải rút gọn:

AB =

AD = BC = 4,4 (cm).

IV. GIẢI BÀI TẬP CUỐI SGK

Giải chi tiết bài 1 trang 86 sgk toán 9 tập 1 cánh diều

Tìm x, y trong mỗi hình 23a, 23b, 23c (làm tròn kết quả đến hàng phần mười của centimét).

Lời giải rút gọn:

a)

b)

c)

y = .

Giải chi tiết bài 2 trang 86 sgk toán 9 tập 1 cánh diều

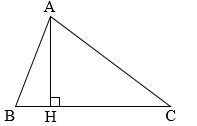
Cho tam giác ABC có đường cao AH = 6 cm, Tính độ dài các đoạn thẳng AB, BH, AC, BC (làm tròn kết quả đến hàng phần mười của centimét).

Lời giải rút gọn:

(cm)

BC = BH + HC = 7,2 + 8,6 = 15,8 (cm).

Giải chi tiết bài 3 trang 86 sgk toán 9 tập 1 cánh diều

Cho tam giác ABC vuông tại A có Chứng minh AC =

Lời giải rút gọn:

Gọi M là trung điểm của BC

Mà

Mà

Mà

Giải chi tiết bài 4 trang 87 sgk toán 9 tập 1 cánh diều

Cho tam giác ABC vuông cân tại A. Chứng minh AB = AC =

Lời giải rút gọn:

Vì tam giác ABC vuông tân tại A

Vậy AB = AC = .

Giải chi tiết bài 5 trang 87 sgk toán 9 tập 1 cánh diều

Trong Hình 24, cho và Chứng minh:

a) OA = m.cot

b) AC = m.cos

c) CD = m.

Lời giải rút gọn:

a)

b) Ta có (cùng phụ góc )

cos

c) Ta có (cùng phụ góc )

cos

Mà

Vậy CD = .

Hay CD = m.

Giải chi tiết bài 6 trang 87 sgk toán 9 tập 1 cánh diều

Tính độ dài đường gấp khúc ABCDEGH (làm tròn kết quả đến hàng phần mười của centimét), bết các tam giác OB, OBC, OCD, ODE, OEG, OGH là các tam giác vuông tại các đỉnh lần lượt là B, C, D, E, G, H; và các góc O₁, O₂, O₃, O₄, O₅, O₆ đều bằng 30 và OA = 2 cm (Hình 25).

Lời giải rút gọn:

sin 30

sin 30

DO =

DE = DO.

EO =

EG = EO.sin 30

OG =

GH = OG. sin 30 =

Độ dài đường gấp khúc ABCDEGH = AB + BC + CD + DE + EG + GH 

= 1 + + +

=

Giải chi tiết bài 7 trang 87 sgk toán 9 tập 1 cánh diều

Hình 26 minh họa một phần con sông có bề rộng AB = 100 m. Một chiếc thuyền đi thẳng từ vị trí B bên này bờ sông đến vị trí C bên kia bờ sông. Tính qunagx đường BC (làm tròn kết quả đến hàng phần mười của mét), biết = 35.

Lời giải rút gọn:

Theo hình vẽ ta có:

cos

Vậy quãng đường BC là 122,1 m.

Giải chi tiết bài 8 trang 87 sgk toán 9 tập 1 cánh diều

Từ vị trí A ở phía tên một tòa nhà có chiều cao AD = 68 m, bác Duy nhìn thấy vị trí C cao nhất của một tháp truyền hình, góc tạo bởi tia AC và tia AH theo phương nằm gang là = 43. Bác Duy cũng nhìn thấy chân tháp tại vị trí B mà góc tạo bởi tia AB và tia AH là = 28, điểm H thuộc đoạn thẳng BC (Hình 27). Tính khoảng cách BD từ chân tháp đến chân tòa nhà và chiều cao BC của tháp truyền hình (làm tròn kết quả đến hàng phần mười của mét).

Lời giải rút gọn:

= 90 –

Xét vuông tại D

cos

AH = BD = 127,9 (m)

AD = BH = 68 (m)

Xét vuông tại H

BC = CH + BH = 119,3 + 68 =187,3 (m) 

Vậy khoảng cách BD từ chân tháp đến chân tòa nhà là 127,9 (m) và chiều cao BC của tháp truyền hình là 187,3 (m).