Slide bài giảng Toán 9 Cánh diều bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác

Tóm lược nội dung

BÀI 1. ĐƯỜNG TRÒN NGOẠI TIẾP TAM GIÁC. ĐƯỜNG TRÒN NỘI TIẾP TAM GIÁC

Mở đầu Trong thiết kế logo ở Hình 1, đường tròn đi qua ba đỉnh của tam giác. 

Đường tròn đi qua ba đỉnh của tam giác được gọi là gì ?

Lời giải rút gọn:

Đường tròn ngoại tiếp tam giác.

I. ĐƯỜNG TRÒN NGOẠI TIẾP TAM GIÁC 

Hoạt động 1 trang 68 toán 9 tập 2 cánh diều

Cho biết các đỉnh của tam giác ABC(Hình 2) có thuộc đường tròn (O) hay không?

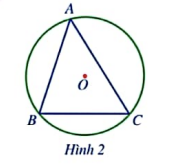
Lời giải rút gọn:

Các đỉnh A, B, C của tam giác ABC có thuộc đường tròn (O)

Luyện tập, vận dụng 1 trang 69 toán 9 tập 2 cánh diều

Quan sát Hình 4 và cho biết trong hai đường tròn (O) và (I), đường tròn nào ngoại tiếp tam giác ABC, đường tròn nào ngoại tiếp tam giác ABD?

Lời giải rút gọn:

Đường tròn (O) là đường tròn ngoại tiếp tam giác ABC 

Đường tron (I) là đường tròn ngoại tiếp tam giác ABD

Hoạt động 2 trang 69 toán 9 tập 2 cánh diều

Cho tam giác ABC có O là giao điểm của ba đường trung trực (Hình 5).

a) Các đoạn thẳng OA,OB và OC có bằng nhau hay không?

b) Đặt R = OA. Đường tròn (O;R) có phải đường tròn ngoại tiếp tam giác ABC không? Vì sao?

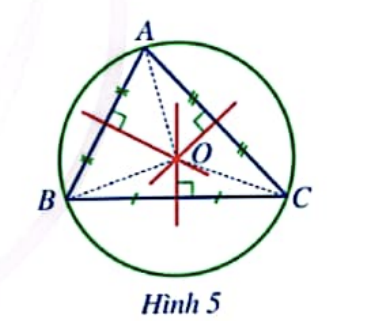
Lời giải rút gọn:

a) Xét tam giác ABC ta có:

OA = OB(tính chất đường trung trực)

OA = OC(tính chất đường trung trực)

OB = OC(tính chất đường trung trực)

=> OA = OB = OC hay ba đoạn thẳng OA, OB và OC là bằng nhau.

b) Đường tròn tâm O bán kính R có R = OA = OB = OC => (O;R) đi qua ba đỉnh của tam giác ABC nên đường tròn (O;R) là đường tròn ngoại tiếp tam giác ABC.

Hoạt động 3 trang 70 toán 9 tập 2 cánh diều 

Cho tam giác ABC vuông tại A. Gọi O là trung điểm của BC(Hình 7). Đường tròn (O;OB) có phải là đường tròn ngoại tiếp của tam giác ABC hay không?

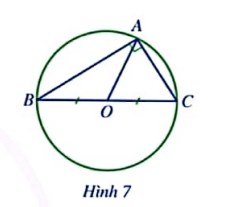
Lời giải rút gọn:

Ta có O là trung điểm của BC => OA là đường trung tuyến của tam giác ABC vuông tại A.

(tính chất trung tuyến trong tam giác vuông)

Đường tròn (O;OB) đi qua ba đỉnh của tam giác ABC nên đường tròn (O; OB) là đường tròn ngoại tiếp tam giác ABC.

Luyện tập, vận dụng 2 trang 70 toán 9 tập 2 cánh diều 

Nêu cách sử dụng ê ke để xác định tâm của một đường tròn bất kì khi chưa biết tâm của nó.

Lời giải rút gọn:

Bước 1: Chọn một điểm bất kì trên đường tròn, ta gọi điểm đó là điểm M.

Bước 2: Đặt đỉnh vuông góc của ê ke trùng với điểm M, sau đó vạch một đường thẳng đi qua cạnh huyền của ê ke, đường thẳng này sẽ cắt đường tròn tại hai điểm A và B.

Bước 3: Giữ nguyên vị trí đỉnh vuông góc của ê ke tại M, xoay ê ke một goác 90 độ. Vạch một đường thẳng khác đi qua cạnh huyền của ê ke, đường thẳng này sẽ cắt đường tròn tại hai điểm C và D.

Bước 4: Giao điểm của hai đường thẳng AB và CD chính là tâm O của đường tròn.

Hoạt động 4 trang 70 toán 9 tập 2 cánh diều

Cho tam giác đều ABC cạnh a, ba đường trung tuyến AM,BN,CP cắt nhau tại trọng tâm O(Hình 8).

a) AM,BN,CP có là các đường trung trực của tam giác ABC hay không?

b) Điểm O có là tâm đường tròn ngoại tiếp tam giác ABC hay không?

c) Tính AM theo a.

d) Tính OA theo a.

Lời giải rút gọn:

a) Ta có AB = AC (ABC là tam giác đều), M là trung điểm của BC (AM là đường trung tuyến) => AM là đường trung trực của tam giác ABC.

BA = BC(ABC là tam giác đều), N là trung điểm của AC(BN là đường trung tuyến) => BN là đường trung trực của tam giác ABC.

CA = CB(ABC là tam giác đều), P là trung điểm của AB(CP là đường trung tuyến) =>CP là đường trung trực của tam giác ABC.

b) Ta có AM,BN,CP là các đường trung trực của tam giác ABC

=> OA = OB = OC( tính chất đường trung trực)

=> O là tâm đường tròn ngoại tiếp tam giác ABC vì (O) đi qua ba đỉnh của tam giác ABC.

c) M là trung điểm BC => MC = .BC =

Áp đụng định lí Pi-ta-go cho tam giác AMC vuông tại M (AM là đường trung trực):

<=>  

<=> AM =

d) O là trọng tâm của tam giác ABC => AO = AM

<=> AO =

Luyện tập, vận dụng 3 trang 71 toán 9 tập 2 cánh diều

Cho tam giác đều ABC nội tiếp đường tròn (O; 2cm). Tính AB.

Lời giải rút gọn:

Gọi AB là a

Bán kinh đường tròn ngoại tiếp là 2 =

=> a =

II. ĐƯỜNG TRÒN NỘI TIẾP TAM GIÁC 

Hoạt động 5 trang 71 toán 9 tập 2 cánh diều 

Cho tam giác ABC và đường tròn (I) ( Hình 9). Nêu vị trí tương đối của các đường thẳng AB,BC,CA với đường tròn (I).

Lời giải rút gọn:

Đường thẳng AB,BC,CA tiếp xúc với đường tròn (I).

Luyện tập, vận dụng 4 trang 72 toán 9 tập 2 cánh diều 

Trong hình 11, đường tròn (I) là đường tròn nội tiếp những tam giác nào?

Lời giải rút gọn:

Đường tròn (I) là đường tròn nội tiếp tam giác ABC và tam giác DEC.

Hoạt động 6 trang 72 toán 9 tập 2 cánh diều 

Cho tam giác ABC có I là giao điểm của ba đường phân giác. Gọi M,N,P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB (Hình 12).

a) So sánh các đoạn thẳng IM,IN và IP.

b) Đặt r = IM. Đường tròn (I;r) có phải là đường tròn nội tiếp tam giác ABC hay không? Vì sao?

Lời giải rút gọn:

a) Xét tam giác BPI và tam giác BMI có:

Góc BPI = góc BMI = 90 độ

Góc PBI = góc MBI(BI là tia phân giác)

=> Tam giác BPI = tam giác BMI( cạnh huyền - góc nhọn)

=> IP = IM

Tương tự, tam giác API bằng tam giác ANI => IP = IN

=> IM = IN = IP

b) r = IM = IN = IP 

=> đường tròn (I;r) là đường tròn nội tiếp tam giác ABC.

Luyện tập, vận dụng 5 trang 73 toán 9 tập 2 cánh diều 

Cho tam giác đều ABC ngoại tiếp đường tròn (O;6) cm. Tính AB.

Lời giải rút gọn:

Gọi a = AB

Bán kính đường tròn nội tiếp là 6 =

=> a = 36/ =

III. GIẢI BÀI TẬP CUỐI SGK

Giải rút gọn bài 1 trang 73 sgk toán 9 tập 2 cánh diều 

Trong các hình 15a,15b,15c,15d, ở hình nào ta có đường tròn (O) là đường tròn ngoại tiếp tam giác ABC? Ở hình nào ta có đường tròn (O) là đường tròn nội tiếp tam giác ABC? Vì sao?

Lời giải rút gọn:

Đường tròn (O) đi qua ba đỉnh của tam giác => đường tròn (O) là đường tròn ngoại tiếp tam giác ABC.

Ba cạnh của tam giác tiếp xúc với đường tròn (O) => đường tròn (O) là đường tròn nội tiếp tam giác ABC.

Giải rút gọn bài 2 trang 74 sgk toán 9 tập 2 cánh diều 

Tính bán kính đường tròn ngoại tiếp tam giác ABC vuông tại A, biết AB = 5cm, AC = 12cm.

Lời giải rút gọn:

13

=> OB =

Vậy bán kính đường tròn ngoại tiếp tam giác ABC là 6,5cm.

Giải rút gọn bài 3 trang 74 sgk toán 9 tập 2 cánh diều 

Cho bán kính đường tròn nội tiếp tam giác đều bằng 4cm. Tính cạnh của tam giác đều đó.

Lời giải rút gọn:

r =.

Giải rút gọn bài 4 trang 74 sgk toán 9 tập 2 cánh diều 

Một chiếc máy quay ở đài truyền hình được đặt trên giá đỡ ba chân, các điểm tiếp xúc với mặt đất của ba chân lần lượt là ba đỉnh A,B,C của tam giác đều ABC( Hình 16). Tính khoảng cách giữa hai vị trí A và B, biết bán kính đường tròn ngoại tiếp tam giác ABC là 4dm.

Lời giải rút gọn:

Tam giác đều cạnh a có bán kính đường ròn ngoại tiép là

Gọi khoảng cách giữa A và B là a

Bán kính đường tròn ngoại tiếp tam giác ABC là 4=

<=>  a=

Giải rút gọn bài 5 trang 74 sgk toán 9 tập 2 cánh diều 

Cho tam giác nhọn ABC(AB<AC) nội tiếp đường tròn (O) đường kính AD=2R. Gọi M là trung điểm cạnh BC và H là trực tâm của tam giác ABC. Chứng minh:

a) DB ⊥ AB và CD ⊥AC;

b) Tứ giác BHCD là hình bình hành;

c)  

d) Ba điểm H,M,D thẳng hàng và AH = 2OM;

Lời giải rút gọn:

a)  (góc chắn đường kính)

=> DB ⊥ AB(dpcm)

(góc chắn đường kính)

=> CD ⊥AC(dpcm)

b)Ta có BF ⊥ AC; DC ⊥ AC => DC//BF hay DC//HB(1)

Có CE ⊥ AB; DB ⊥ AB => CE//BD hay CH//BD        (2)

Từ 1 và 2 suy ra tứ giác BHCD là hình bình hành

c) BHCD là hình bình hành => DC = BH

Xét ΔADC vuông tại C ta có:

.

Mà =

(dpcm)

d) BHCD là hình bình hành, M là trung điểm của BC

=>  H,D,M thẳng hàng

Giải rút gọn bài 6 trang 74 sgk toán 9 tập 2 cánh diều 

Cho tứ giác ABCD có các tam giác ABC và ADC lần lượt ngoại tiếp các đưởng tròn (I) và (K) sao cho hai đường tròn này cùng tiếp xúc với đường thẳng AC tại điểm H thuộc đoạn thẳng AC. Giả sử đường tròn (I) tiếp xúc với cạnh AB tại M, đường tròn (K) tiếp xúc với cạnh AD tại N( hình 17). Chứng minh:

a) Ba điểm I,H, K thẳng hàng.

b) AM = AN.

c)

Lời giải rút gọn:

a) AC tiếp xúc với đường tròn (I) => IH⊥AC(tính chất tiếp tuyến)

AC tiếp xúc với đường tròn (K) => HK⊥AC(tính chất tiếp tuyến)

=> I,H,K thẳng hàng.

b) AB,AC tiếp xúc với đường tròn (I) => AB, AC là tiếp tuyến của đường tròn (I) => AH = AM (tính chất tiếp  tuyến) (1)

AD,AC tiếp xúc với đường tròn (K) => AD, AC là tiếp tuyến của đường tròn (K) => AH = AN(tính chất tiếp  tuyến) (2)

Từ 1 và 2 => AM = AH = AN hay AM = AN

c) Đường tròn (I) nội tiếp tam giác ABC => AI là tia phân giác của

=>

Đường tròn (K) nội tiếp tam giác ADC => AK là tia phân giác của

=>

Mà

=>=