Slide bài giảng Toán 9 Cánh diều bài 3: Tiếp tuyến của đường tròn

Tóm lược nội dung

BÀI 3. TIẾP TUYẾN CỦA ĐƯỜNG TRÒN

Mở đầu: Quan sát máy cắt máy cắt sắt đang hoạt động (Hình 32), ta thấy các mảnh vụn sắt chuyển động và văng ra theo phương tiếp tuyến với đường tròn mép đĩa sắt. Tiếp tuyến của đường tròn có tính chất gì và được nhận biết như thế nào?

Lời giải rút gọn:

Vuông góc với bán kính đi qua tiếp điểm.

I. NHẬN BIẾT TIẾP TUYẾN CỦA ĐƯỜNG TRÒN

Hoạt động 1 trang 106 sgk toán 9 tập 1 cánh diều

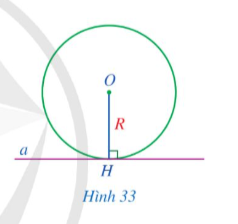
Cho đường thẳng a là tiếp tuyến của đường tròn (O; R). Gọi H là hình chiếu của tâm O trên đường thẳng a (Hình 33).

a) So sánh khoảng cách OH từ tâm O đến đường thẳng a và bán kính R.

b) Điểm H có thuộc đường tròn (O; R) hay không?

c) Điểm H có phải là tiếp điểm của đường thẳng a và đường tròn (O; R) hay không?

d) Đường thẳng a có vuông góc với bán kính đi qua tiếp điểm hay không?

Lời giải rút gọn:

a) Khoảng cách từ OH từ tâm O đến đường thẳng a bằng bán kính R

b) Điểm H thuộc đường tròn (O; R)

c) Điểm H là tiếp điểm của đường thẳng a và đường tròn (O; R)

d) Đường thẳng a vuông góc với bán kính và đi qua tiếp điểm.

Luyện tập, vận dụng 1 trang 107 sgk toán 9 tập 1 cánh diêu

Cho ba điểm A, B, C thẳng hàng, trong đó B nằm giữa A và C. Đường tròn (O) tiếp xúc với đường thẳng AB tại điểm C. Chứng minh

Lời giải rút gọn:

Đường tròn (O) tiếp xúc với đường thẳng AB tại C nên OC vuông góc AB tại C

= 90

Xét  vuông tại C ta có:

Hoạt động 2 trang 107 sgk toán 9 tập 1 cánh diều

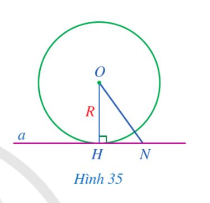
Cho đường thẳng a và đường tròn (O; R) thỏa mãn đường thẳng a đi qua điểm H thuộc đường tròn (O;R) và a vuông góc với OH. Lấy điểm N thuộc đường thẳng a và N khác H (Hình 35).

a) So sánh khoảng cách từ điểm O đến đường thẳng a và bán kính R.

b) So sánh ON và R. Điểm N có thuộc đường tòn (O; R) hay không?

c) Đường thẳng a có phải là tiếp tuyến của đường tròn (O; R) hay không?

Lời giải rút gọn:

a) Bằng nhau.

b) Xét vuông tại H. ON là cạnh huyền

ON > OH hay ON > R.

c) Đường thẳng a là tiếp tuyến của đường tròn (O; R)

Luyện tập, vận dụng 2 trang 107 toán 9 tập 1 cánh diều

Cho hai đường tròn (O; R) và (O’; R’) tiếp xúc ngoài nhau tại điểm I. Gọi d là tiếp tuyến của (O; R) tại điểm I. Chứng minh d là tiếp tuyến của (O’; R’).

Lời giải rút gọn:

d là tiếp tuyến của (O; R) tại I

Mà IO’

là tiếp tuyến của đường tròn (O’; R’).

Luyện tập, vận dụng 3 trang 108 sgk toán 9 tập 1 cánh diều

Cho hai đường tròn (O), (O’) cắt nhau tại điểm A, B sao cho đường thẳng OA là tiếp tuyến của đường tròn (O’). Chứng minh đường thẳng O’B là tiếp tuyến của đường tròn (O).

Lời giải rút gọn:

(O) và (O’) cắt nhau tại A, B nên

Xét

OA = OB (bán kính của (O))

OA’ = OB’ (bán kính của (O’))

OO’ chung

                                  (1)

Vì OA là tiếp tuyến của đường (O’)  =   (2)

Từ (1) và (2):

Vậy O’B là tiếp tuyến của đường tròn (O).

II. TÍNH CHẤT CỦA HAI TIẾP TUYẾN CẮT NHAU

Hoạt động 3 trang 108 sgk toán 9 tập 1 cánh diều

Cho đường tròn (O; R). Các đường thẳng c, d lần lượt tiếp xúc với đường tròn (O; R) tại A, B và cắt nhau tại M (Hình 38).

a) Các tam giác MOA và MOB có bằng nhau hay không?

b) Hai đoạn thẳng MA và MB có bằng nhau hay không?

c) Tia MO có phải là tia phân giác của góc AMB hay không?

d) Tia OM có phải là tia phân giác của góc AOB hay không?

Lời giải rút gọn:

a)

b)

c)

d)

Luyện tập, vận dụng 4 trang 109 sgk toán 9 tập 1 cánh diều

Cho đường tròn (O; R) và điểm M nằm ngoài đường tròn. Hai đường thẳng c, d qua M lần lượt tiếp xúc với (O) tại A, B. Biết  = 120. Chứng minh AB = R.

Lời giải rút gọn:

Xét tứ giác AMBO 

 (1)

Xét  (2)

Từ (1) và (2) suy ra

Vậy OA = OB = AB = R (đpcm).

III. GIẢI BÀI TẬP CUỐI SGK

Giải rút gọn bài 1 trang 109 sgk toán 9 tập 1 cánh diều

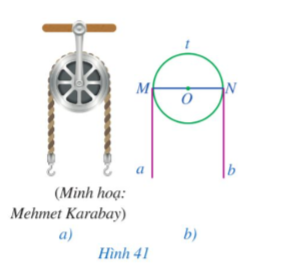
Ròng rọc là một loại máy cơ đơn giản có rãnh và có thể quay quanh một trục, được sử dụng rộng rãi trong công việc nâng lên và hạ xuống vật nặng trong cuộc sống. Trong Hình 41a, có một sợi dây không dãn vắt qua ròng rọc.

Gả sử ròng rọc được minh họa bởi đường tròn (O) sợi dây vắt qua ròng rọc được minh họa bởi nửa đường tròn MtN và hai tiếp tuyến Ma, Nb của đường tròn (O) (Hình 41b). Chứng minh Ma // Nb.

Lời giải rút gọn:

Ma là tiếp tuyến

Nb là tiếp tuyến

Ròng rọc quay quanh trục nên M, O, N thẳng hàng

Ma ( cùng .

Giải rút gọn bài 2 trang 110 sgk toán 9 tập 1 cánh diều

Cho đường tròn (O) và dây AB. Điểm M nằm ngoài đường tròn (O) thỏa mãn điểm B nằm trong góc MAO và Chứng minh đường thẳng MA là tiếp tuyến của đường tròn (O).

Lời giải rút gọn:

OA = OB

Xét

2 + 2= 180

+ = 90

= 90

Vậy MA là tiếp tuyến của đường tròn (O)

Giải rút gọn bài 3 trang 110 sgk toán 9 tập 1 cánh diều

Cho đường tròn (O) và điểm M nằm ngoài đường tròn. Hai đường thẳng c, d đi qua M lần lượt tiếp xúc với (O) tại A, B. Tia phân giác của góc MAB cắt MO tại I. Chứng minh điểm I cách đều ba đường thẳng MA, MB và AB.

Lời giải rút gọn:

AI là đường phân giác của  (gt)

I là trọng tâm của

Nên I cách đều MA, AB, MB (đpcm).

Giải rút gọn bài 4 trang 110 sgk toán 9 tập 1 cánh diều

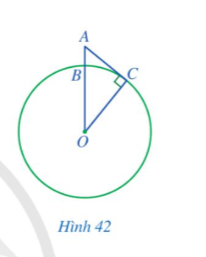
Một người quan sát đặt mắt ở vị trí A có độ cao cách mực nước biển là AB = 5m. Cắt bề mặt trái đất bởi một mặt phẳng đi qua điểm A và tâm của Trái Đất thì phần chung giữa chúng là một đường tròn lớn tâm O. Tầm quan sát tối đa từ vị trí A là đoạn thẳng AC, trong đó C là tiếp điểm của tiếp tuyến đi qua A với đường tròn (O) (minh họa nhu Hình 42). Tính độ dài đoạn thẳng AC (theo đơn vị kilômét và làm tròn kết quả đến hàng phần mười), biết bán kính Trái Đất là OB = OC

(Nguồn: Toán 9 – Tập một, NXB giáo dục Việt Nam, năm 2017).

Lời giải rút gọn:

Xét

Mà OB = OC

Thay vào biểu thức ta được:

Vậy AC khoảng 253 km.

Giải rút gọn bài 5 trang 110 sgk toán 9 tập 1 cánh diều

Cho đường tròn (O; R) đường kính AB và các đường thẳng m, n, p lần lượt tiếp xúc với đường tròn tại A, B, C (Hình 43). Chứng minh:

a) AD + BE = DE;

b)

c) Tam giác ODE vuông;

d) .

Lời giải rút gọn:

a)

AD = CD; CE = BE

(đpcm)

b) DA, DC là tiếp tuyến của đường tròn nên DO là đường phân giác của

Vậy

EB, EC là tiếp tuyến của đường tròn nên EO là đường phân giác của

Vậy

c) Ta có

Mà  =

=

2 + 2 = 180

+  = 90

= 90

Vậy ODE vuông tại O 

 d) Ta có OD.OE = OC.OD (Hệ thức trong tam giác vuông); OC = R

Vậy .