Giải câu 2 trang 119 sách toán VNEN lớp 7 tập 1

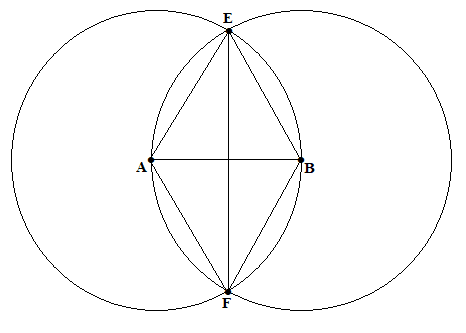
a) Xét $\bigtriangleup ABE$ và $\bigtriangleup ABF$ có:

AB: chung;

AE = AF (bán kính đường tròn tâm A);

BE = BF (bán kính đường tròn tâm B);

Vậy: $\bigtriangleup ABE = \bigtriangleup ABF$ (đpcm).

b) Xét $\bigtriangleup AEF$ và $\bigtriangleup BEF$ có:

EF: chung;

AE = BE = AB (hai đường tròn cùng bán kính);

AF = BF (hai đường tròn cùng bán kính);

Vậy: $\bigtriangleup AEF = \bigtriangleup BEF$ (đpcm).

c) + Chứng minh AE // BF:

$\bigtriangleup ABE = \bigtriangleup ABF$ (theo câu a) $\Rightarrow $ $\widehat{ABE} = \widehat{ABF}$ (hai góc tương ứng bằng nhau). (1)

Xét $\bigtriangleup AFB$ có: AF = BF (Hai đường tròn cùng bán kính) $\Rightarrow $ $\widehat{BAF} = \widehat{ABF}$ (2)

Từ (1) và (2) suy ra: $\widehat{ABE} = \widehat{BAF}$.

Vậy AE // BF (hai góc so le trong bằng nhau).

+ Chứng minh tương tự: AF // BE.