Giải câu 1 trang 113 sách toán VNEN lớp 7 tập 1
C. Hoạt động luyện tập
Câu 1: Trang 113 sách toán VNEN lớp 7 tập 1
Thực hiện các hoạt động sau
a) Quan sát hình 59 và điền vào chỗ trống (…)

Nếu $\bigtriangleup ABC = \bigtriangleup EFD$ thì $\widehat{F} = …$; AB = …..
b) Quan sát các hình 60a và 60b, các cạnh bằng nhau được đánh dấu bởi các kí hiệu giống nhau. Viết kí hiệu thể hiện sự bằng nhau của 2 tam giác có trên hình đó.
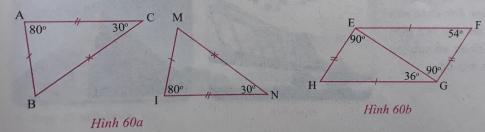
- Ở hình 60a:
$\bigtriangleup ABC$ có $\widehat{A} + \widehat{B} + \widehat{C} = 180^{\circ}$ (định lí tổng ba góc trong tam giác).
$\bigtriangleup INM$ có $\widehat{I} + \widehat{M} + \widehat{N} = 180^{\circ}$ (định lí tổng ba góc trong tam giác).
Mà $\widehat{A} = \widehat{I} = 80^{\circ}; \widehat{C} = \widehat{N} = 30^{\circ}$ (theo hình vẽ) $\Rightarrow \widehat{B} = \widehat{M} = 70^{\circ}$.
Xét $\bigtriangleup ABC$ và $\bigtriangleup INM$ có:

$\Rightarrow $ $\bigtriangleup ABC =\bigtriangleup IMN$.
- Em hãy làm tương tự với hình 60b vào vở.
a) Nếu $\bigtriangleup ABC = \bigtriangleup EFD$ thì $\widehat{F} = \widehat{B}$; AB = EF.
b)
- Ở hình 60b:
$\bigtriangleup EHG$ có $\widehat{E} + \widehat{H} + \widehat{G} = 180^{\circ}$ (định lí tổng ba góc trong tam giác).
$\widehat{HEG} = 90^{circ}; \widehat{EGH} = 36^{circ} \Rightarrow \widehat{EHG} = 54^{circ}$.
$\bigtriangleup GEF$ có $\widehat{G} + \widehat{E} + \widehat{F} = 180^{\circ}$ (định lí tổng ba góc trong tam giác).
$\widehat{EGF} = 90^{circ}; \widehat{EFG} = 54^{circ} \Rightarrow \widehat{FEG} = 36^{circ}$.
Xét $\bigtriangleup EGH$ và $\bigtriangleup GEF$ có:

$\Rightarrow $ $\bigtriangleup EGH =\bigtriangleup GEF$.
Xem toàn bộ: Giải VNEN toán hình 7 bài 1: Hai tam giác bằng nhau

Bình luận