Giải bài tập 44 trang 104 SBT toán 8 tập 1 cánh diều:

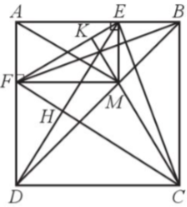
Gọi H là giao điểm của DE và CF, K là giao điểm của CM và EF (Hình 60).

Do ABCD là hình vuông nên ta có:

$\widehat{DAB}$ = 90°, CD = DA, $\widehat{ADB}=\widehat{ABD}=\widehat{DBC}$ = 45°.

a) Do MF ⊥ AD nên tam giác FDM vuông tại F.

Do FM ⊥ AD, DC ⊥ AD nên FM // CD => $\widehat{FMD}=\widehat{MDC}$ (hai góc so le trong).

Mà $\widehat{FDM}=\widehat{MDC}$ (do ABCD là hình vuông nên DM là phân giác góc ADC).

=> $\widehat{FDM}=\widehat{FMD}$ nên ∆FDM vuông cân tại F

=> FM = DF.

Tứ giác AEMF có $\widehat{MFA}=\widehat{FAE}=\widehat{AEM}$ = 90° nên AEMF là hình chữ nhật => AE = FM.

Do đó AE = DF (vì cùng bằng FM).

∆ADE = ∆DCF (c.g.c) => DE = CF, $\widehat{AED}=\widehat{DFC}$.

Trong tam giác ADE vuông tại A, ta có: $\widehat{AED}+\widehat{ADE}$ = 90°.

=> $\widehat{DFC}+\widehat{ADE}$ = 90° hay $\widehat{DFH}+\widehat{FDH}$ = 90°. 

Vậy DE ⊥ CF.

b*) Tương tự câu a, ta chứng minh được BF ⊥ CE.

∆ABM = ∆CBM (c.g.c) => AM = CM.

Mà EF = AM (vì AEMF là hình chữ nhật) => EF = CM.

∆DEF = ∆FCM (c.c.c) => $\widehat{DEF}=\widehat{FCM}$ hay $\widehat{FEH}=\widehat{FCK}$.

Trong tam giác HEF vuông tại H, ta có $\widehat{FEH}+\widehat{EFH}$ = 90°.

Suy ra $\widehat{FCK}+\widehat{EFH}$ = 90° hay $\widehat{FCK}=\widehat{KCF}$ = 90°. 

Từ đó, ta tính được $\widehat{CKF}$ = 90°. Do đó CK ⊥ EF.

Trong tam giác CEF, ta có: DE ⊥ CF, BF ⊥ CE, CM ⊥ EF nên ba đường thẳng DE, BF, CM là các đường cao của tam giác CEF. 

Vậy ba đường thẳng DE, BF, CM cùng đi qua một điểm.

c*) Chu vi của hình chữ nhật AEMF là: 2(AE + AF) = 2(DF + AF) = 2AD. 

Mà AD không đổi nên chu vi của hình chữ nhật AEMF không đổi. 

Do đó, diện tích của tứ giác AEMF lớn nhất khi AEMF là hình vuông.  => ME = MF. 

Khi đó ∆BEM = ∆DFM (cạnh góc vuông - góc nhọn kề) => BM = DM hay M là trung điểm của BC.

Vậy với M là trung điểm của BC thì diện tích của tứ giác AEMF lớn nhất.