Giải bài tập 39 trang 103 SBT toán 8 tập 1 cánh diều:
Bài tập 39 trang 103 SBT toán 8 tập 1 cánh diều:
Cho tứ giác ABCD có E, F, G, H lần lượt là trung điểm của AB, BC, CD, DA. Điều kiện của tứ giác ABCD để tứ giác EFGH là hình chữ nhật là:
A. BD = AC. B. AB ⊥ BC. C. BD ⊥ AC. D. AB = CD.
Chọn đáp án C.
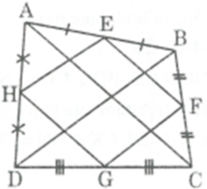
Xét ΔABC có E là trung điểm của AB; F là trung điểm của BC
Do đó: EF là đường trung bình của ΔABC.
=> EF // AC và EF = $\frac{AC}{2}$ (1).
Xét ΔCDA có G là trung điểm của CD; H là trung điểm của DA
Do đó: GH là đường trung bình của ΔCDA.
=> GH // AC và GH = $\frac{AC}{2}$ (2).
Từ (1) và (2) suy ra EF // GH và EF = GH hay EFGH là hình bình hành.
Để EFGH là hình chữ nhật khi hình bình hành EFGH có EF ⊥ EH hay EF ⊥ BD => AC ⊥ BD.
Xem toàn bộ: Giải SBT Toán 8 Cánh diều bài Bài tập cuối chương V
Giải những bài tập khác
Giải bài tập những môn khác
Giải sgk lớp 8 cánh diều
Giải SBT lớp 8 kết nối tri thức
Giải SBT lớp 8 chân trời sáng tạo
Soạn SBT lớp 8 cánh diều
Trắc nghiệm 8 Kết nối tri thức
Trắc nghiệm 8 Chân trời sáng tạo
Trắc nghiệm 8 Cánh diều
Bộ đề thi, đề kiểm tra lớp 8 chân trời sáng tạo
Giáo án lớp 8
Bình luận