Giải bài tập 42 trang 104 SBT toán 8 tập 1 cánh diều:

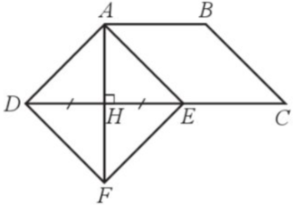
a) Do ABCD là hình thang cân nên $\widehat{C}=\widehat{ADC}$.

∆ADH = ∆AEH (c.g.c) => $\widehat{ADH}=\widehat{AEH}$ hay $\widehat{ADC}=\widehat{AED}$. 

Do đó $\widehat{C}=\widehat{AED}$. Mà $\widehat{C},\widehat{AED}$ nằm ở vị trí đồng vị => AE // BC.

Tứ giác ABCE có AB // CE, AE // BC nên ABCE là hình bình hành.

b) Ta có: $\widehat{FDH}=\widehat{AEH}$ (hai góc so le trong).

∆FDH = ∆AEH (g.c.g) => AH = HF.

Tứ giác ADFE có hai đường chéo AF và DE cắt nhau tại trung điểm H của mỗi đường nên ADFE là hình bình hành.

Tam giác ADE có $\widehat{AED}=\widehat{ADE}$ = 45° nên tam giác ADE vuông cân tại A.

Hình bình hành ADFE có $\widehat{DAE}$ = 90° nên ADFE là hình chữ nhật.

Hình chữ nhật ADFE có AD = AE nên ADFE là hình vuông.

c*) Để E là trung điểm của BF thì BE = FE và ba điểm B, E, F thẳng hàng.

Khi bỏ qua giả thiết $\widehat{ADC}$ = 45° thì ta chỉ chứng minh được ADFE là hình bình hành.

Do ABCE và ADFE đều là hình bình hành nên AE = BC và AE = DF => BC = DF.

Ta có: $\widehat{FDH}=\widehat{BCD}$ (vì cùng bằng $\widehat{AEH}$) và $\widehat{FDH},\widehat{BCD}$ nằm ở vị trí so le trong nên BC // DF.

Tứ giác BCFD có BC = DF và BC // DF nên BCFD là hình bình hành. 

Mà E là trung điểm của BF => E là trung điểm của CD hay EC = ED

Mặt khác, AB = EC (vì ABCE là hình bình hành) => AB = $\frac{1}{2}$CD.

Dễ thấy nếu hình thang cân ABCD (AB // CD) có AB = $\frac{1}{2}$CD thì E là trung điểm của BF.

Vậy điều kiện của hình thang cân ABCD (AB // CD) để E là trung điểm của BF là AB = $\frac{1}{2}$CD.