Giải bài tập 43 trang 76 SBT toán 8 tập 2 cánh diều:

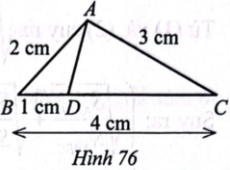
Trên đoạn thẳng BC lấy điểm D sao cho BD = 1cm => CD = BC – BD = 3 cm. 

Tam giác ADC có CD = CA = 3 cm nên là tam giác cân tại C, do đó $\widehat{DAC}=\widehat{ADC}$ (1).

Xét hai tam giác ABD và CBA, ta có: $\widehat{DBA}=\widehat{ABC}$, $\frac{BD}{BA}=\frac{AB}{CB}=\frac{1}{2}$

=> ΔABD ᔕ ΔCBA. Do đó $\widehat{BAD}=\widehat{BCA}$ (2). 

Từ (1) và (2), ta có:

$\widehat{BAC}=\widehat{BAD}+\widehat{DAC}=\widehat{BCA}+\widehat{ADC}$

$=\widehat{BCA}+\widehat{BAD}+\widehat{ABD}=\widehat{ABC}+2\widehat{BCA}$.

Vậy $\widehat{BAC}=\widehat{ABC}+2\widehat{BCA}$.