Giải bài tập 41 trang 75 SBT toán 8 tập 2 cánh diều:
Bài tập 41 trang 75 SBT toán 8 tập 2 cánh diều:
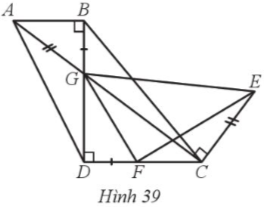
Hình thang ABCD ở Hình 39 có AB // CD, AB < CD, $\widehat{ABD}$ = 90°. Hai đường chéo AC và BD cắt nhau tại G. Điểm E nằm trên đường vuông góc với AC tại C thỏa mãn CE = AG và đoạn thẳng GE không cắt đường thẳng CD. Điểm F nằm trên đoạn thẳng DC và DF = GB. Chứng minh:
a) ΔFDG ᔕ ΔECG;
b) ΔGDC ᔕ ΔGFE;
c) $\widehat{GFE}$ = 90°.
a) Do AB // CD nên $\frac{BG}{AG}=\frac{GD}{GC}$.
Mặt khác AG = CE, BG = DF nên $\frac{DF}{CE}=\frac{GD}{GC}$.
Mà $\widehat{GDF}=\widehat{GCE}$ nên ΔFDG ᔕ ΔECG.
b) Vì ΔFDG ᔕ ΔECG nên $\widehat{DGF}=\widehat{CGE}$ và $\frac{DG}{GF}=\frac{GC}{GE}$.
$\widehat{DGF}=\widehat{CGE}$ => $\widehat{DGF}+\widehat{FGC}=\widehat{CGE}+\widehat{FGC}$
Hay $\widehat{DGC}=\widehat{FGE}$.
Từ đó, ta có ΔGDC ᔕ ΔGFE vì $\frac{DG}{GF}=\frac{GC}{GE}$ và $\widehat{DGC}=\widehat{FGE}$.
c) Vì ΔGDC ᔕ ΔGFE nên $\widehat{GFE}=\widehat{GDC}$ = 90°.
Giải những bài tập khác
Giải bài tập những môn khác
Giải sgk lớp 8 cánh diều
Giải SBT lớp 8 kết nối tri thức
Giải SBT lớp 8 chân trời sáng tạo
Soạn SBT lớp 8 cánh diều
Trắc nghiệm 8 Kết nối tri thức
Trắc nghiệm 8 Chân trời sáng tạo
Trắc nghiệm 8 Cánh diều
Bộ đề thi, đề kiểm tra lớp 8 chân trời sáng tạo
Giáo án lớp 8
Bình luận