Giải bài tập 32 trang 102 SBT toán 8 tập 1 cánh diều:

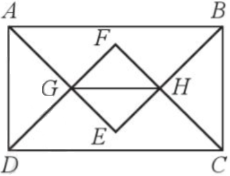
a) Do ABCD là hình chữ nhật nên

$\widehat{DAB}=\widehat{ABC}=\widehat{BCD}=\widehat{CDA}$ = 90°.

Mà AE, BE, CF, DF lần lượt là các tia phân giác của các góc DAB, ABC, BCD, CDA

=>$\widehat{DAE}=\widehat{EAB}=\widehat{ABE}=\widehat{EBC}=\widehat{BCF}=\widehat{FCD}=\widehat{CDF}=\widehat{FDA}= 45°$.

Do đó, các tam giác EAB, FCD, GAD, HBC đều là tam giác vuông cân. 

∆GAD = ∆HBC (g.c.g) => GD = HC.  Mà FD = FC => FG = FH. 

Do đó, tam giác FGH vuông cân tại F => $\widehat{FGH}$ = 45°.

Ta có: $\widehat{FGH}=\widehat{CDF}$ = 45° và $\widehat{FGH}$, $\widehat{CDF}$ nằm ở vị trí đồng vị nên GH // CD. 

b) $\widehat{EGF}=\widehat{AGD}$ = 90° (hai góc đối đỉnh).

Tứ giác GFHE có $\widehat{EGF}=\widehat{GFH}=\widehat{HEG}$ = 90° nên GFHE là hình chữ nhật.

Hình chữ nhật GFHE có FG = FH nên GFHE là hình vuông.