Trắc nghiệm Toán 12 Kết nối bài Hoạt động thực hành trải nghiệm: Tính nguyên hàm và tích phân với phần mềm GeoGebra. Tính gần đúng tích phân bằng phương pháp hình thang (P2)
Bộ câu hỏi và Trắc nghiệm Toán 12 kết nối tri thức bài Hoạt động thực hành trải nghiệm: Tính nguyên hàm và tích phân với phần mềm GeoGebra. Tính gần đúng tích phân bằng phương pháp hình thang (P2) có đáp án. Học sinh luyện tập bằng cách chọn đáp án của mình trong từng câu hỏi. Dưới cùng của bài trắc nghiệm, có phần xem kết quả để so sánh kết quả bài làm của mình. Kéo xuống dưới để bắt đầu.
TRẮC NGHIỆM
Câu 1: Bạn Nam muốn sử dụng phần mềm GeoGebra để tính đạo hàm của hàm số ![]() . Bạn Nam cần thao tác thế nào?
. Bạn Nam cần thao tác thế nào?
A. IntegralSymbolic(
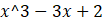 ).
).- B. Symbolic(
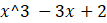 )
) - C.
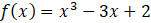 , IntegralSymbolic (x).
, IntegralSymbolic (x). - D. Nlntegral (f(x)).
Câu 2: Khi sử dụng phần mềm GeoGebra để tính tích phân của hàm số ![]() từ
từ ![]() đến
đến ![]() , ta cần nhập lệnh:
, ta cần nhập lệnh:
A. Nlntegral(
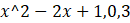 )
)- B. Nlntegral(
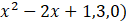 .
. - C. Nlntegral(
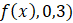 .
. - D.Nlntegral(
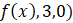 .
.
Câu 3: Để tính nguyên hàm của hàm số ta dùng lệnh:
- A. IntergarlSymbolic.
- B. Symbolic.
C. IntergarlSymbolic ().
- D. Nlntegral ().
Câu 4: Để tính giá trị gần đúng của tích phân, ta dùng lệnh:
- A. Tegral ().
B. Nlntegral ().
- C. Symbolic ().
- D. IntergarlSymbolic ().
Câu 5: Tính gần đúng tích phân sau ![]() với
với![]()
A. 0,981
- B. 1,25
- C. 0,871.
- D. 0,871.
Câu 6: Tính gần đúng tích phân ![]() với
với ![]() .
.
- A.
 .
. - B.
 .
. - C.
 .
. D.
 .
.
Câu 7: Phương pháp hình thang là một phương pháp số học dùng để tính gần đúng tích phân của một hàm số. Hãy chọn câu trả lời đúng về phương pháp này:A. Song song với mặt đất.
- A. Phương pháp hình thang sử dụng đoạn chia đều trên trục tung và tính diện tích của các hình tam giác nhỏ để xấp xỉ diện tích dưới đường cong.
- B. Phương pháp hình thang sử dụng đoạn chia đều trên trục hoành và tính diện tích của các hình chữ nhật nhỏ để xấp xỉ diện tích dưới đường cong.
- C.Phương pháp hình thang tính giá trị của hàm số tại các điểm chia và sau đó tính trung bình của các giá trị này để xấp xỉ diện tích dưới đường cong.
D. Phương pháp hình thang chia đoạn tích phân thành các đoạn nhỏ, sử dụng hình thang để tính diện tích dưới đường cong trên mỗi đoạn, sau đó cộng tổng diện tích của các hình thang nhỏ để xấp xỉ diện tích dưới đường cong.
Câu 8: Để tính xấp xỉ ![]() với độ chính xác không vượt quá số
với độ chính xác không vượt quá số ![]() cho trước, ta thực hiện các bước:
cho trước, ta thực hiện các bước:
(1) Với sai số ![]() cho trước, tìm số tự nhiên
cho trước, tìm số tự nhiên ![]() (nhỏ nhất) sao cho
(nhỏ nhất) sao cho ![]() .
.
(2) Tính ![]() và tìm
và tìm ![]() .
.
(3) Chia đoạn ![]() thành
thành ![]() đoạn con có độ dài bằng nhau và áp dụng công thức hình thang.
đoạn con có độ dài bằng nhau và áp dụng công thức hình thang.
A. (2); (1); (3).
- B. (1); (2); (3).
- C. (3); (2); (1).
- D.(3); (1); (2).
Câu 9: Một chiếc xe ô tô chạy thử nghiệm trên một đường thẳng bắt đầu từ trạng thái đứng yên. Tốc độ của chiếc xe ô tô đó (tính bằng mét/giây) được ghi lại trong bảng sau:
| Thời gian (giây) | 0 | 10 | 20 | 30 | 40 | 50 | 60 |
| Tốc độ (mét/giây) | 0 | 5 | 21 | 40 | 62 | 78 | 83 |
Hãy tính gần đúng quãng đường mà xe ô tô đó đã đi được tính đến giây thứ 60 của quá trình thử nghiệm theo phương pháp hình thang.
- A.
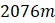 .
. - B.
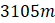 .
. C.
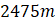 .
.- D.
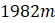 .
.
Câu 10: Đo cường độ dòng điện ![]() qua một mạch điện tại các thời diểm cách đều nhau 1s trong 10s, ta thu được các kết quả ghi trong bảng sau:
qua một mạch điện tại các thời diểm cách đều nhau 1s trong 10s, ta thu được các kết quả ghi trong bảng sau:

Dùng công thức hình thang tính gần đúng điện lượng ![]() chuyển qua đoạn mạch trong thời gian từ
chuyển qua đoạn mạch trong thời gian từ ![]() đến
đến ![]() .
.
- A.
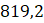 .
. B.
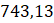 .
.- C.
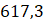 .
. - D.
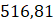 .
.
Nội dung quan tâm khác
Giải bài tập những môn khác
Môn học lớp 12 KNTT
5 phút giải toán 12 KNTT
5 phút soạn bài văn 12 KNTT
Văn mẫu 12 KNTT
5 phút giải vật lí 12 KNTT
5 phút giải hoá học 12 KNTT
5 phút giải sinh học 12 KNTT
5 phút giải KTPL 12 KNTT
5 phút giải lịch sử 12 KNTT
5 phút giải địa lí 12 KNTT
5 phút giải CN lâm nghiệp 12 KNTT
5 phút giải CN điện - điện tử 12 KNTT
5 phút giải THUD12 KNTT
5 phút giải KHMT12 KNTT
5 phút giải HĐTN 12 KNTT
5 phút giải ANQP 12 KNTT
Môn học lớp 12 CTST
5 phút giải toán 12 CTST
5 phút soạn bài văn 12 CTST
Văn mẫu 12 CTST
5 phút giải vật lí 12 CTST
5 phút giải hoá học 12 CTST
5 phút giải sinh học 12 CTST
5 phút giải KTPL 12 CTST
5 phút giải lịch sử 12 CTST
5 phút giải địa lí 12 CTST
5 phút giải THUD 12 CTST
5 phút giải KHMT 12 CTST
5 phút giải HĐTN 12 bản 1 CTST
5 phút giải HĐTN 12 bản 2 CTST
Môn học lớp 12 cánh diều
5 phút giải toán 12 CD
5 phút soạn bài văn 12 CD
Văn mẫu 12 CD
5 phút giải vật lí 12 CD
5 phút giải hoá học 12 CD
5 phút giải sinh học 12 CD
5 phút giải KTPL 12 CD
5 phút giải lịch sử 12 CD
5 phút giải địa lí 12 CD
5 phút giải CN lâm nghiệp 12 CD
5 phút giải CN điện - điện tử 12 CD
5 phút giải THUD 12 CD
5 phút giải KHMT 12 CD
5 phút giải HĐTN 12 CD
5 phút giải ANQP 12 CD
Giải chuyên đề học tập lớp 12 kết nối tri thức
Giải chuyên đề Ngữ văn 12 Kết nối tri thức
Giải chuyên đề Toán 12 Kết nối tri thức
Giải chuyên đề Vật lí 12 Kết nối tri thức
Giải chuyên đề Hóa học 12 Kết nối tri thức
Giải chuyên đề Sinh học 12 Kết nối tri thức
Giải chuyên đề Kinh tế pháp luật 12 Kết nối tri thức
Giải chuyên đề Lịch sử 12 Kết nối tri thức
Giải chuyên đề Địa lí 12 Kết nối tri thức
Giải chuyên đề Tin học ứng dụng 12 Kết nối tri thức
Giải chuyên đề Khoa học máy tính 12 Kết nối tri thức
Giải chuyên đề Công nghệ 12 Điện - điện tử Kết nối tri thức
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Kết nối tri thức
Giải chuyên đề học tập lớp 12 chân trời sáng tạo
Giải chuyên đề Ngữ văn 12 Chân trời sáng tạo
Giải chuyên đề Toán 12 Chân trời sáng tạo
Giải chuyên đề Vật lí 12 Chân trời sáng tạo
Giải chuyên đề Hóa học 12 Chân trời sáng tạo
Giải chuyên đề Sinh học 12 Chân trời sáng tạo
Giải chuyên đề Kinh tế pháp luật 12 Chân trời sáng tạo
Giải chuyên đề Lịch sử 12 Chân trời sáng tạo
Giải chuyên đề Địa lí 12 Chân trời sáng tạo
Giải chuyên đề Tin học ứng dụng 12 Chân trời sáng tạo
Giải chuyên đề Khoa học máy tính 12 Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Điện - điện tử Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Chân trời sáng tạo
Giải chuyên đề học tập lớp 12 cánh diều
Giải chuyên đề Ngữ văn 12 Cánh diều
Giải chuyên đề Toán 12 Cánh diều
Giải chuyên đề Vật lí 12 Cánh diều
Giải chuyên đề Hóa học 12 Cánh diều
Giải chuyên đề Sinh học 12 Cánh diều
Giải chuyên đề Kinh tế pháp luật 12 Cánh diều
Giải chuyên đề Lịch sử 12 Cánh diều
Giải chuyên đề Địa lí 12 Cánh diều
Giải chuyên đề Tin học ứng dụng 12 Cánh diều
Giải chuyên đề Khoa học máy tính 12 Cánh diều
Giải chuyên đề Công nghệ 12 Điện - điện tử Cánh diều
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Cánh diều

Bình luận