Câu 1: Cho hàm số y = $x^{4} + 4x^{2} + 3$ có đồ thị (C). Tìm số giao điểm của (C) và trục hoành.

• A. 3
• B. 2
• C. 1

• D. 0

Câu 2: Tìm đạo hàm của hàm số y = log₂(x+1)

• A. y' = $\frac{1}{x+1}$
• B. y' = $\frac{ln2}{x+1}$

• C. y' = $\frac{1}{(x+1)ln2}$

• D. y' = $\frac{1}{2ln(x+1)}$

Câu 3: Tìm tập nghiệm S của bất phương trình $log (2x - 2)$ $\geq$ $log (x + 1)$

• A. (3; = $\infty$)
• B. (1; 3]

• C. [3; + $\infty$)

• D. Vô nghiệm 

Câu 4: Hàm số y = $\frac{2x + 3}{x + 1}$ có bao nhiêu điểm cực trị?

• A. 3

• B. 0

• C. 2
• D. 1

Câu 5: Tìm giá trị nhỏ nhất m của hàm số y = $x^{2}$ + $\frac{x}{2}$ trên đoạn [$\frac{1}{2}$; 2]

• A. m = $\frac{17}{4}$
• B. m = 0
• C. m = 5

• D. m = 3

Câu 6: Cho hàm số y = $\frac{3x - 1}{x + 1}$. Mệnh đề nào dưới đây là đúng?

• A. Hàm số đồng biến trên các khoảng (-$\infty$; -1) và (-1; +$\infty$)

• B. Hàm số luôn luôn đồng biến trên R \ {-1}
• C. Hàm số nghịch biến trên các khoảng (-$\infty$; -1) và (-1; +$\infty$)
• D. Hàm số luôn luôn nghịch biến trên R \ {-1}

Câu 7: Bảng biến thiên sau đây là của hàm số nào?

• A. y = $x^{4}$ - 3$x^{2}$ + 1
• B. y = - $x^{4}$ + 3$x^{2}$ + 1

• C. y = $x^{4}$ + 3$x^{2}$ + 1

• D. y = - $x^{4}$ - 3$x^{2}$ + 1

Câu 8: Cho hàm số y = $\sqrt[]{2x^{2}+1}$. Mệnh đề nào dưới đây đúng?

• A. Hàm số nghịch biến trên khoảng (-1;1)

• B. Hàm số đồng biến trên khoảng (0; +$\infty$)

• C. Hàm số đồng biến trên khoảng (-$\infty$; 0)
• D. Hàm số nghịch biến trên khoảng (0; +$\infty$)

Câu 9: Tìm tất cả các giá trị của hàm số m để phương trình -$x^{4}$ + 2$x^{2}$ = m có bốn nghiệm thực phân biệt.

• A. m > 0
• B. 0 $\leq$  m $\leq$ 1

• C. 0 < m < 1

• D. m < 1

Câu 10: Một vật chuyển động theo quy luật s = - $\frac{1}{3}$ $t^{3}$ + 6 $t^{2}$ với t (giây) là khoảng thời gian tính từ khi vật bắt đầu chuyển động và s (mét) là quãng đường vật di chuyển được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 9 giây, kể từ khi bắt đầu chuyển động, vận động lớn nhất của vật đạt được là bao nhiêu?

• A. 144 (m/s)

• B. 36 (m/s)

• C. 243 (m/s)
• D. 27 (m/s)

Câu 11: Đồ thị hàm số y = $\frac{x-2}{x^{2}-3x+2}$ có bao nhiêu tiệm cận?

• A. 0
• B. 3
• C. 1

• D. 2

Câu 12: Tính giá trị của biểu thức K = $\frac{2^{3}.2^{-1}+5^{-3}.5^{4}}{10^{-3}:10^{-2} - (0,25)^{0}}$ là

• A. -10

• B. 10
• C. 12
• D. 15

Câu 13: Cho P = $log_{\frac{1}{a}}\sqrt[3]{a^{7}}$ (a>0, a \neq 1). Mệnh đề nào dưới đây đúng?

• A. P = $\frac{7}{3}$ 
• B. P = $\frac{5}{3}$ 
• C. P = $\frac{2}{3}$ 

• D. P = - $\frac{7}{3}$ 

Câu 14: Hàm số nào dưới đây nghịch biến trên khoảng (-$\infty$ ;+$\infty$).

• A. y = $x^{3}$ - 3 $x^{2}$
• B. y = $x^{4}$ + 4 $x^{2}$ + 2017
• C. y = - $x^{3}$ + 3 $x^{2}$ + 1

• D. y = $\frac{x + 5}{x + 1}$

Câu 15: Cho 0 < a < 1. Mệnh đề nào dưới các mệnh đề sau là SAI?

• A. $log_{a}x$ > 0 khi 0 < x < 1
• B. $log_{a}x$ < 0 khi x > 1

• C. Nếu x₁ < x₂ thì $log_{a}x_{1}$ < $log_{a}x_{2}$

• D. Đồ thị hàm số y = $log_{a}x$ có tiệm cận đứng là trục tung

Câu 16: Cho (H) là khối chóp tứ giác đều có các cạnh bằng a. Thể tích của (H) bằng.

• A. $\frac{a^{3}}{3}$

• B. $\frac{a^{3}\sqrt{2}}{6}$

• C. $\frac{a^{3}\sqrt{3}}{4}$
• D. $\frac{a^{3}\sqrt{3}}{2}$

Câu 17: Cho hàm số y = $\frac{mx+4m}{x+m}$ với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của m để hàm số nghịch biến trên các khoảng xác định. Tìm số phần tử của S.

• A. 5
• B. 4
• C. Vô số

• D. 3

Câu 18: Tìm tất cả các giá trị của thực của tham số m để đồ thị hàm số y = $mx^{2}$ - 4$mx^{3}$ có hai điểm cực trị A và B sao cho tam giác OAB có diện tích bằng 4 với O là gốc toạ độ.

• A. m = - $\frac{1}{\sqrt[4]{2}}$; m = $\frac{1}{\sqrt[4]{2}}$

• B. m = -1; m = 1

• C. m = 1
• D. m $\neq$ 0

Câu 19: Tìm giá trị lớn nhất của hàm số y = $-x^{3} + 3x + 1$ trên khoảng (0; +$\infty$)?

• A. -1

• B. 3

• C. -3
• D. 4

Câu 20: Trong các mệnh đề sau mệnh đề nào sai?

• A. Lắp ghép hai khối hộp sẽ được một khối đa diện lồi

• B. Khối hộp là khối đa diện lồi
• C. Khối tứ diện là khối đa diện lồi
• D. Khối lăng trụ tam giác là khối đa diện lồi

Câu 21: Tìm nghiệm S của phương trình $log_{2}x + 3 log_{x}2 = 4$ 

• A. S = {2;8}

• B. S = {4;3}
• C. S = {4; 16}
• D. Vô nghiệm

Câu 22: Tìm nghiệm của phương trình log₂(x - 5) = 4

• A. x = 21

• B. x = 3
• C. x = 11
• D. x = 13

Câu 23: Đường cong trong hình vẽ bên là đồ thị của một hàm số bên trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. 

Hỏi đó là hàm số nào?

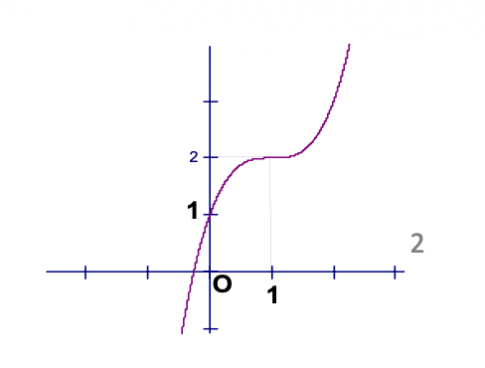
• A. $y = x^{3} - 3x^{2} + 3x + 1$

• B. $y = -x^{3} + 3x^{2} + 1$
• C. $y = 2x^{3} - x + 1$
• D. $y = -x^{3} - 3x^{2} + 1$

Câu 24: Cho a là số thực dương tuỳ ý khác 1. Mệnh đề nào dưới đây đúng?

• A. $log_{2}a = log_{a}2$
• B. $log_{2}a = \frac{1}{log_{2}a}$

• C. $log_{2}a = \frac{1}{log_{a}2}$

• D. $log_{2}a = -log_{a}2$

Câu 25: Tìm tập xác định D của hàm số $y = (x^{2}-x-2)^{-3}$

• A. D = $\mathbb{R}$
• B. D = (0; +$\infty$)
• C. D = (-$\infty$; -1) $\cup $ (2; +$\infty$)

• D. D = $\mathbb{R}$\ {-1;2}

Câu 26: Cho hình nón có thể tích bằng V = 36$\pi a^{3}$ và bán kính đáy bằng 3a. Tính độ dài đường cao h của hình nón đã cho.

• A. 4a

• B. 12a

• C. 5a
• D. a

Câu 27: Tìm tất cả các giá trị thực của tham số m để phương trình $3^{x}$ = m có nghiệm thực.

• A. m $\geq$ 1
• B. m $\geq$ 0

• C. m > 0

• D. m $\neq$ 0

Câu 28: Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi S là diện tích xung quanh đường tròn đáy ngoại tiếp hai hình vuông ABCD và A'B'C'D'. Diện tích S là:

• A. $\pi a^{2}$

• B. $\pi a^{2}\sqrt{2}$

• C. $\pi a^{2}\sqrt{3}$
• D. $\frac{\pi a^{2}\sqrt{2}}{2}$

Câu 29: Tìm tập xác định D của hàm số $y = log_{3}(x^{2}-4x+3)$

• A. D = (2-$\sqrt{2}$;1) $\cup $ (3; 2+$\sqrt{2}$)
• B. D = (1;3)

• C. D = (-$\infty$;1) $\cup $ (3; +$\infty$)

• D. D = (-$\infty$; 2-$\sqrt{2}$) $\cup $ (2+$\sqrt{2}$; +$\infty$)

Câu 30: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng 2a, diện tích xung quanh của hình nón đỉnh S và đáy là hình tròn nội tiếp ABCD bằng

• A. $\frac{\pi a^{2}\sqrt{17}}{4}$

• B. $\frac{\pi a^{2}\sqrt{15}}{4}$
• C. $\frac{\pi a^{2}\sqrt{17}}{6}$
• D. $\frac{\pi a^{2}\sqrt{17}}{8}$

Câu 31: Cho hàm số y = f(x) liên trục trên đoạn [-2;2] và có đồ thị là đường cong như hình vẽ bên. TÌm số nghiệm của phương trình |f(x)| = 1 trên đoạn [-2;2]

• A. 4

• B. 6

• C. 3
• D. 5

Câu 32: Cho hình nón có bán kính r = $\sqrt{3}$ và độ dài đường sinh l = 4. Tính diện tích xung quanh $S_{xq}$ của hình nón đã cho.

• A. $S_{xq}$ = 12$\pi$ 

• B. $S_{xq}$ = 4 $\sqrt{3 }$$\pi$ 

• C.  $S_{xq}$ = 12$\pi$
• D. $S_{xq}$ = 8 $\sqrt{3 }$$\pi$ 

Câu 33: Cho $log_{}3=a$ và $log_{}5=b$. Tính $log_{6}1125$.

• A. $\frac{3a+2b}{a-1+b}$

• B. $\frac{2a+3b}{a+1-b}$

• C. $\frac{3a+2b}{a+1-b}$
• D. $\frac{3a-2b}{a+1+b}$

Câu 34: Cho hình bát diện đều cạnh a. Gọi S là tổng diện tích tất cả các mặt của bát diện đều đó. Mệnh đề nào dưới đây đúng?

• A. S = $4\sqrt{3}a^{2}$
• B. S = $\sqrt{3}a^{2}$

• C. S = $2\sqrt{3}a^{2}$

• D. S = $8a^{2}$

Câu 35: Hỏi phương trình $2^{x+\sqrt{2x+5}}-2^{1+\sqrt{2x+5}}+2^{6-x}-32=0$ có bao nhiêu nghiệm phân biệt?

• A. 2

• B. 1
• C. 3
• D. 4

Câu 36: Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB = a, AD = 2a, SA = $a\sqrt{3}$, SA vuông góc (ABCD). M là điểm trên SA sao cho AM = $\frac{a\sqrt{3}}{3}$. Tính thể tích của khối chóp S.BMC

• A. $\frac{2a^{3}\sqrt{3}}{9}$

• B. $\frac{2a^{3}\sqrt{3}}{3}$
• C. $\frac{4a^{3}\sqrt{3}}{3}$
• D. $\frac{3a^{3}\sqrt{2}}{9}$

Câu 37: Với mọi a, b, x là các số thực dương thoả mãn $log_{2}x=5^{2}a+3log_{2}b$. Mệnh đề dưới đây đúng?

• A. x = 3a+5b
• B. x= 5a+3b
• C. x = $a^{5}+b^{3}$

• D. x = $a^{5}+b^{3}$

Câu 38: Cho khối chóp tam giác S.ABC có cạnh đáy bằng a và cạnh bên bằng 2a. Tính thể tích V của khối chóp S.ABC.

• A. V = $\frac{\sqrt{13}a^{3}}{12}$ 

• B. V = $\frac{\sqrt{11}a^{3}}{12}$

• C. V =$\frac{\sqrt{11}a^{3}}{6}$
• D. V =$\frac{\sqrt{11}a^{3}}{4}$

Câu 39: Gọi l, h, R lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình nón. Đẳng thức nào sau đây luôn đúng.

• A. $l^{2}=h^{2}+R^{2}$

• B. $\frac{1}{l^{2}}=\frac{1}{h^{2}}+\frac{1}{R^{2}}$
• C. $R^{2}=h^{2}+l^{2}$
• D. $l^{2}=hR$

Câu 40: Hàm số f(x) = ln x có đạo hàm cấp n là:

• A. $f^{(n)}(x)=\frac{n}{x^{n}}$

• B. $f^{(n)}(x)=(-1)^{n+1}\frac{(n-1)!}{x^{n}}$

• C. $f^{(n)}(x)=\frac{1}{x^{n}}$
• D. $f^{(n)}(x)=\frac{n!}{x^{n}}$

Câu 41: Gọi l, h, R lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của khối nói (N). Thể tích V của khối nón (N) bằng

• A. V = $\frac{1}{3}\pi R^{2}h$
• B. V = $\pi R^{2}h$
• C. V = $\frac{1}{3}\pi R^{2}l$
• D. V = $\frac{1}{3}\pi R^{2}l$

Câu 42: Tìm giá trị thực của tham số m để phương trình $9^{x}-2.3^{x+1}+m=0$ có hai nghiệm thực $x_{1}$, $x_{2}$ thoả mãn $x_{1}$ + $x_{1}$ = 1

• A. m = 6

• B. m = -3
• C. m = 3
• D. m = 1 

Câu 43: Cho khối chóp S.ABCD có đáy ABCD có nửa lục giác đều nội tiếp trong nửa đường tròn đường kính AB = 2R, cạnh bên SD vuông góc với đáy, mặt (SBC) hợp với ABCD một góc 45 độ. Tính thể tích khối chóp S.ABCD

• A. $\frac{\sqrt{3}R^{3}}{2}$

• B. $3R^{3}$
• C. $\frac{3R^{3}}{6}$
• D. $\frac{3R^{3}}{2}$

Câu 44: Tìm giá trị thực của tham số m để đường thẳng d: y = (2m-1)x + 3 + m vuông góc với đường thẳng đi qua hai điểm cực trị của hàm số y = $x^{3}-3^{2}+1$.

• m = $\frac{2}{3}$

• m = $\frac{3}{4}$

• m = $\frac{1}{2}$
• m = $\frac{1}{4}$

Câu 45: Hỏi có bao nhiêu giá trị m nguyên trong đoạn [-2017;2017] để phương trình $log_{3}m + log^{3}x = 2 log_{3}(x+1)$ luôn có 2 nghiệm phân biệt?

• A. 4015
• B. 2010
• C. 2018

• D. 2013

Câu 46: Hàm số $y = 4\sqrt{x^{2}-2x+3}+2x-x^{2}$ đạt giá trị lớn nhất tại hai giá trị x mà tích của chúng là:

• A. 2
• B. 1
• C. 0

• D. -1

Câu 47: Tìm tất cả các giá trị thực của tham số m để hàm số $y=ln(x^{2}-2x+m+1)$ có tập xác định là

• A. m = 0
• B. 0 < m < 3
• C. m < -1 hoặc m > 0

• D. m > 0

Câu 48: Anh Nam gửi 100 triệu đồng vào ngân hàng Vietcombank. Lãi suất hàng năm không thay đổi là 7,5%/năm. Nếu anh Nam hàng năm không rút lãi thì sau 5 năm số tiền anh Nam nhận được cả vốn lẫn tiền lãi (kết quả làm tròn đến hàng ngàn) là

• A. 143.563.000 đồng

• B. 2.373.047.000 đồng
• C. 137.500.500 đồng
• D. 133.547.000 đồng 

Câu 49: Cho một tấm bìa hình vuông cạnh 5dm. Để làm một mô hình kim tự tháp Ai Cập, người ta cắt bỏ bốn tam giác cân bằng nhau có cạnh đáy chính là cạnh của hindh vuông rồi gấp lên, ghép lại thành một hình chóp tứ giác đều. Để mô hình có thể tích lớn nhất thì cạnh đáy của mô hình là: 

• A. $\frac{3\sqrt{2}}{2}$
• B. $\frac{5}{2}$
• C. $\frac{5\sqrt{2}}{2}$

• D. $2\sqrt{2}$

Câu 50: Cho tam giác ABC vuông cân tại A có AB = AC = 12. Lấy một điểm M thuộc cạnh huyền BC và gọi H là hình chiếu của M lên cạnh góc vuông AB. Quay tam giác AMH quanh trục là đường thẳng AB tạp thành mặt nón tròn xoay (N), hỏi thể tích V của khối nón tròn xoay (H) lớn nhất là bao nhiêu? 

• A. V = $\frac{256\pi }{3}$

• B. V = $\frac{128\pi }{3}$
• C. V = 256$\pi$ 
• D. V = 72$\pi$