BÀI TẬP ÔN TẬP CUỐI NĂM

A. TRẮC NGHIỆM

Bài 1: Cho hệ bất phương trình bậc nhất hai ẩn . Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình đã cho?

A. (1; 1)                B. (2; 0)           C. (3; 2)                D. (3; -2).

Đáp án:

C

Bài 2: Cho tam giác ABC. Có bao nhiêu điểm M thỏa mãn + = 3 ?

A. Vô số               B. 1                 C. 2                       D. 3

Đáp án:

A

Bài 3: Biết rằng parabol y = x² +bx + c có đỉnh là I(1; 4). Khi đó giá trị của b + c là

A. 1                    B. 2                   C. 3                      D. 4.

Đáp án:

C                                      

Bài 4: Trong mặt phẳng tọa độ Oxy, cho đường thẳng Δ: x + 2y -5 = 0. Tìm mệnh đề sai trong các mệnh đề sau:

A. Vectơ =(1;2) là một vectơ pháp tuyến của Δ

B.  Vectơ =(2;−1) là một vectơ chỉ phương của Δ.

C. Đường thẳng Δ song song với đường thẳng d:

D. Đường thẳng Δ có hệ số góc k = 2.

Đáp án:

D

Bài 5: Trong khai triển nhị thức Newton của (2 + 3x)⁴, hệ số của x² là:

A. 9                   B.               C. 9.                   D. 36.

Đáp án:

D

Bài 6: Một tổ gồm 7 nam và 3 nữ. Chọn ngẫu nhiên hai người. Xác suất để trong hai người được chọn có ít nhất một nữ là:

A. .                     B. .                             C. .                     D. .

Đáp án:

B

B. TỰ LUẬN

Bài 7: Cho các mệnh đề:

P: "Tam giác ABC là tam giác vuông tại A";

Q: "Tam giác ABC có các cạnh thỏa mãn AB² + AC² = BC²"

a. Hãy phát biểu các mệnh đề P ⇒ Q, Q ⇒ P, P ⇔ Q, ⇒ . Xét tính đúng sai của các mệnh đề này.

b. Dùng các khái niệm "điều kiện cần" và "điều kiện đủ" để diễn rả mệnh đề P ⇒ Q.

c. Gọi X là tập hợp các tam giác ABC vuông tại A, Y là tập hợp các tam giác ABC có trung tuyến AM=BC. Nêu mối quan hệ giữa hai tập hợp X và Y.

Đáp án: 

a.

• P ⇒ Q: Nếu tam giác ABC là tam giác vuông tại A thì tam giác ABC có các cạnh thỏa mãn AB² + AC² = BC².

• Q ⇒ P: Nếu tam giác ABC có các cạnh thỏa mãn AB² + AC² = BC² thì tam giác ABC là tam giác vuông tại A.

• P ⇔ Q: Tam giác ABC là tam giác vuông tại A khi và chỉ khi tam giác ABC có các cạnh thỏa mãn AB² + AC² = BC².

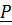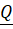• ⇒ : Nếu tam giác ABC không là tam giác vuông tại A thì tam giác ABC có các cạnh thỏa mãn AB² + AC² ≠ BC².

b.

• Tam giác ABC là tam giác vuông tại A là điều kiện đủ để tam giác ABC có các cạnh thỏa mãn AB² + AC² = BC².

• Tam giác ABC có các cạnh thỏa mãn AB² + AC² = BC² là điều kiện cần để tam giác ABC là tam giác vuông tại A.

c. X = Y

Bài 8: a. Biểu diễn miền nghiệm D của hệ bất phương trình bậc nhất hai ẩn sau:

b. Từ kết quả câu a, tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F(x; y) = 2x + 3y trên miền D.

Đáp án:

a. 

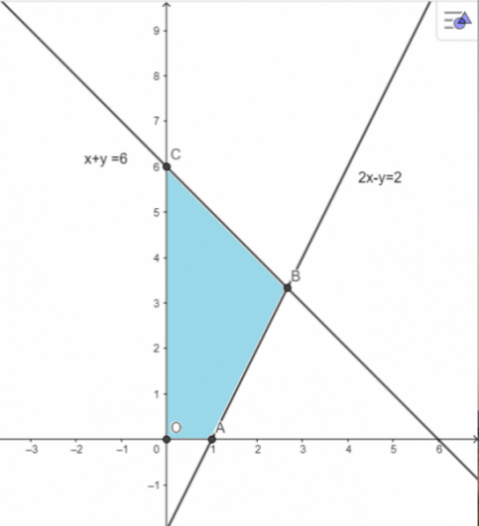
b.

• Giá trị lớn nhất của F trên miền D là: F(0; 6) = 18

• Giá trị nhỏ nhất của E trên miền D là: F(0; 0) = 0

Bài 9: Cho hàm số y = f(x) = ax² + bx + c với đồ thị là parabol (P) có đỉnh I() 

và đi qua điểm A(1; 2).

a. Biết rằng phương trình của parabol có thể viết dưới dạng y = a(x - h)² + k, trong đó I(h, k) là tọa độ đỉnh của parabol. Hãy xác định phương trình của parabol (P) đã cho và vẽ parabol này.

b. Từ parabol (P) đã vẽ ở câu a, hãy cho biết khoảng đồng biến và khoảng nghịch biến của hàm số y=f(x).

c. Giải bất phương trình f(x) ≥ 0.

Đáp án: 

a. y = x² -5x +6.

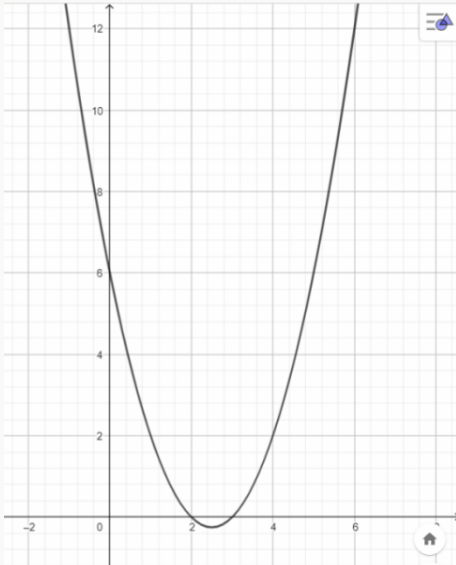
b.

• Hàm số f(x) đồng biến trên khoảng: (;+∞)

• Hàm số f(x) nghịch biến trên khoảng: (−∞;).

c.  x ≥ 3 hoặc x ≤ 2.

Bài 10: Giải các phương trình chứa căn thức sau:

a.

b.

Đáp án:

a. vô nghiệm

b. x = 5+

Bài 11: Từ các chữ số 0; 1; 2;.....; 9 có thể lập được tất cả bao nhiêu số tự nhiên nhỏ hơn 1000, chia hết cho 5 và gồm các chữ số khác nhau?

Đáp án:

155 số

Bài 12: Viết khai triển nhị thức Newton của (2x -1)ⁿ, biết n là số tự nhiên thỏa mãn + 24 = 140

Đáp án:

32x⁵ - 80x⁴ + 80x³ - 40x² + 10x -1. 

Bài 13: Từ các công thức tính diện tích tam giác đã được học, hãy chứng minh rằng, trong tam giác ABC, ta có:

r

Đáp án:

S_ABC =

Mà: p - a = ; p - b =;  p - c

⇒ rS_ABC : p =

Bài 14: Cho hình vuông ABCD có cạnh bằng a. Gọi M, N tương ứng là trung điểm của các cạnh AB, BC.

a. Biểu thị các vectơ ,  theo các vectơ ,

b. Tính  . và tìm góc giữa hai đường thẳng DM và AN.

Đáp án:

a. ;   

b.  = 0 => góc giữa đường thẳng DM và AN là 90^o.

Bài 15: Trong mặt phẳng tọa độ, cho tam giác ABC có ba đỉnh A(-1; 3), B(1; 2), C(4; -2).

a. Viết phương trình đường thẳng BC.

b. Tính diện tích tam giác ABC.

c. Viết phương trình đường tròn có tâm A và tiếp xúc với đường thẳng BC.

Đáp án:

a.  4x+3y−10=0

b. S_ABC =

c) (x + 1)² + (y – 3)² = 1. 

Bài 16: Trên mặt phẳng tọa độ, hai vật thể khởi hành cùng lúc tại hai điểm A(1; 1) và B(-1; 21) với các vectơ vận tốc tương ứng là =(1;2), =(1;−4). Hỏi hai vật thể đó có gặp nhau không?

Đáp án:

Hai vật không thể gặp nhau.

Bài 17: Trong đêm, một âm thanh cầu cứu phát ra từ một vị trí trong rừng và đã được hai trạm ghi tín hiệu ở các vị trí A, B nhận được. Khoảng cách giữa hai trạm là 16 km và trạm ở vị trí A nhận được tín hiệu sớm hơn 6 giây so với trạm ở vị trí. Giả sử vận tốc âm thanh là 1236 km/h. Hãy xác định phạm vi tìm kiếm vị trí phát ra âm thanh đó.

Đáp án:

Phạm vi tìm kiếm vị trí phát ra âm thanh đó là nhánh gần A của hypebol (H) có phương trình

Bài 18: Các nhà toán học cổ đại Trung Quốc đã dùng phân số để xấp xỉ cho π.

a. Cho biết đâu là số đúng, đâu là số gần đúng.

b. Đánh giá sai số tuyệt đối, sai số tương đối của giá trị gần đúng này biết: 

3,1415 < π < 3,1416.

Đáp án:

a.Số đúng π;  Số gần đúng

b. Sai số tuyệt đối là 0,0014; Sai số tương đối là 0, 0,00045

Bài 19:  Tỷ lệ hộ nghèo (%) của 10 tỉnh/thành phố thuộc đồng bằng sông Hồng trong năm 2010 và năm 2016 được cho trong bảng sau:

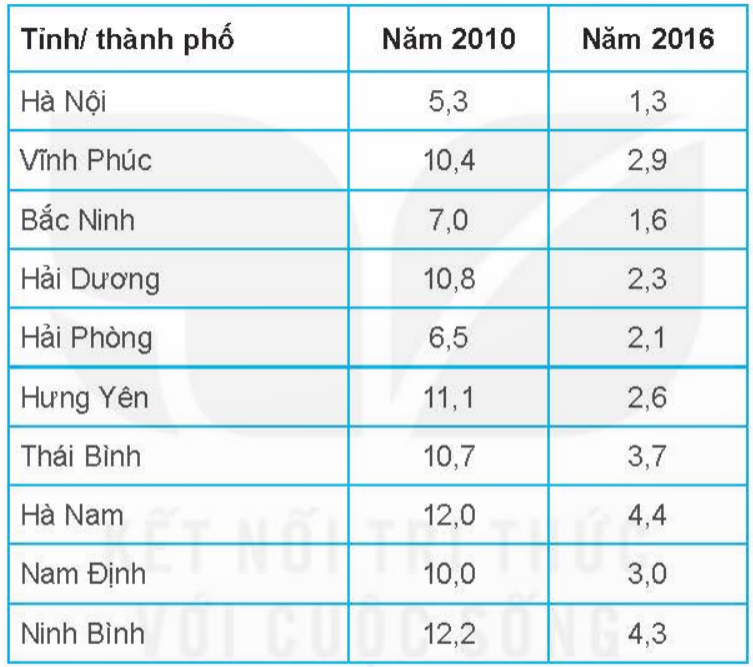
a. Tính số trung bình và độ lệch chuẩn của tỉ lệ hộ nghèo các tỉnh/thành phố thuộc đồng bằng sông Hồng trong các năm 2010, 2016.

b. Dựa trên kết quả nhận được, em có nhận xét gì về số trung bình và độ phân tán của tỉ lệ hộ nghèo các tỉnh/thành phố thuộc đồng bằng sông Hồng trong các năm 2010 và 2016.

Đáp án:

-Năm 2010

            Số trung bình: 9,6; Độ lệch chuẩn : 2,3

-Năm 2016

            Số trung bình  2,82; Độ lệch chuẩn : 1,007

b. Mức độ phân tán của năm 2010 cao hơn năm 2016.

Bài 20: Chọn ngẫu nhiên ba số khác nhau từ 23 số nguyên dương đầu tiên. Tìm xác suất để tổng ba số chọn được là một số chẵn

Đáp án:

P(A)