Slide bài giảng toán 8 cánh diều bài 8: Trường hợp đồng dạng thứ ba của tam giác

Tóm lược nội dung

BÀI 8. TRƯỜNG HỢP ĐỒNG DẠNG THỨ BA CỦA TAM GIÁC

I. TRƯỜNG HỢP ĐỒNG DẠNG THỨ BA : GÓC- GÓC

Luyện tập 1 (Trang 83):

Cho hai tam giác ABC và MNP thỏa mãn = 50⁰ ; = 60⁰; = 60⁰; = 70⁰.Chứng minh △ABC  ᔕ△MNP. 

Trả lời rút gọn:

Tam giác MNP có + + = 180⁰

Mà = 60⁰; = 70⁰ => = 50⁰

Ta có : = = 50⁰ ; = = 60⁰

Suy ra △ABC  ᔕ △MNP (g.g)

II. ÁP DỤNG TRƯỜNG HỢP ĐỒNG DẠNG THỨ BA CỦA TAM GIÁC VÀO TAM GIÁC VUÔNG

Luyện tập 2 (Trang 84):

Cho tam giác nhọn ABC có hai đường cao AD, BE cắt nhau tại H. Chứng minh HA.HD = HB.HE 

Trả lời rút gọn:

Ta có : = = 90⁰ ; = (hai góc đối đỉnh)

Suy ra : △AEH ᔕ △BDH (g.g)

Do đó: = hay HA.HD = HB.HE

BÀI TẬP CUỐI SGK

Bài 1 (Trang 85): 

Cho Hình 86. 

a) Chứng minh △MNP ᔕ △ABC.                          b) Tìm x.

Trả lời rút gọn:

a) Ta có : = = 60⁰ ; = = 45⁰

suy ra △MNP ᔕ △ABC (g.g)

b) △MNP ᔕ △ABC nên = hay = => x = 3

Bài 2 (Trang 85): 

Cho hai tam giác ABC và PMN thỏa mãn = 70⁰ ; = 80⁰; = 80⁰; = 30⁰.Chứng minh = =

Trả lời rút gọn: 

Tam giác MNP có + + = 180⁰

Mà = 80⁰; = 30⁰ => = 70⁰

Ta có : = = 70⁰ ; = = 80⁰

Suy ra △ABC  ᔕ △PMN (g.g)

Do đó = =

Bài 3 (Trang 85): 

Cho tam giác nhọn ABC, hai đường cao AD và BE cắt nhau tại H. Chứng minh:

a) △ACD ᔕ △BCE và CA.CE = CB.CD;

b) △ACD ᔕ △AHE và AC.AE = AD.AH. 

Trả lời rút gọn:

a) Ta có : = = 90⁰; chung góc C

suy ra △ACD ᔕ △BCE (g.g) 

do đó = hay CA.CE = CB.CD

b) Ta có : = = 90⁰; chung góc A

suy ra △ACD ᔕ △AHE (g.g) 

do đó = hay AC.AE = AD.AH

Bài 4 (Trang 85): 

Cho Hình 87 với = . Chứng minh:

a) △OAD ᔕ  △OCB;                b)  =             c) △OAC ᔕ △ODB.

Trả lời rút gọn:

a) Ta có : = ,  chung góc O

suy ra △OAD ᔕ  △OCB( g.g)

b) △OAD ᔕ  △OCB nên =  

hay =

c) = (cmt) và chung góc O => △OAC ᔕ △ODB (c.g.c)

Bài 5 (Trang 85): 

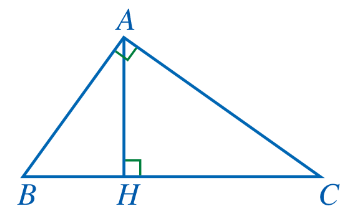
Cho tam giác ABC vuông tại A, đường cao AH (Hình 88). Chứng minh:

a) △ABC  ᔕ△HBA và AB² = BC . BH;

b) △ABC ᔕ △HAC và AC² = BC . CH;

c) △ABH ᔕ △CAH và AH²  = BH . CH;

d) =  

Trả lời rút gọn:

a) Ta có : = = 90⁰; chung góc B

Suy ra △ABC  ᔕ△HBA

Do đó : = hay AB² = BC . BH

b) Ta có : = = 90⁰; chung góc C

Suy ra △ABC  ᔕ△HAC

Do đó : = hay AC² = BC . CH

c) Ta có  △ABC  ᔕ △HBA

Mà △ABC  ᔕ△HAC

Suy ra △ABH  ᔕ△CAH

Do đó = hay AH² = BH. CH

d) Ta có: AB² = BC . BH => =

              AC² = BC . CH => =

               AH² = BH . CH => = (1)

 Ta có : + = + = = = (2)

Từ (1)(2) suy ra : =

Bài 6 (Trang 85): 

Trong Hình 89, bạn Minh dùng một dụng cụ để đo chiều cao của cây. Cho biết khoảng cách từ mắt bạn Minh đến cây và đến mặt đất lần lượt là AH = 2,8 m và AK = 1,6 m. Em hãy tính chiều cao của cây.

Trả lời rút gọn:

Chiều cao của cây là đoạn thẳng BC. 

Ta có: AHBK là hình chữ nhật nên AK = BH = 1,6 m

Tam giác AHB vuông tại H: AB² = AH² + BH² = 2,8² + 1,6² = 10,4 => AB =

Ta có : = = 90⁰; chung góc B

Suy ra : △HBA ᔕ △ABC

Do đó =

Suy ra BC = = 6,5 (m)