Slide bài giảng toán 8 cánh diều bài 4: Tính chất đường phân giác của tam giác

Tóm lược nội dung

BÀI 4. TÍNH CHẤT ĐƯỜNG PHÂN GIÁC CỦA TAM GIÁC

Luyện tập 1 (Trang 67):

Hình 37 minh họa một phần sân nhà bạn Duy được lát bởi các viên gạch hình vuông khít nhau, trong đó các điểm A, B, C, D là bốn đỉnh của một viên gạch. Bạn Duy đặt một thước gỗ trên mặt sân sao cho thước gỗ luôn đi qua điểm C và cắt tia AB tại M, cắt tia AD tại N. Bạn Duy nhận thấy ta luôn có tỉ lệ thức .

Tại sao ta luôn có tỉ lệ thức ?

Trả lời rút gọn:

+ Vì là hình vuông nên là tia phân giác của => là đường phân giác trong .

+ Áp dụng tính chất đường phân giác trong tam giác, ta có :  (đpcm).

Luyện tập 2 (Trang 67):

Cho tam giác ABC có AB < AC, AD là đường phân giác. 

Chứng minh DB < DC. 

Trả lời rút gọn:

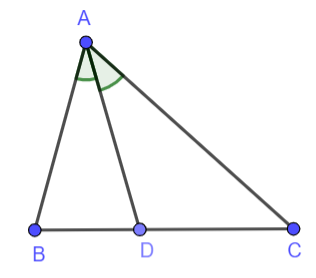
Xét có là đường phân giác=>

Mà => => => .

Luyện tập 3 (Trang 68): 

Cho tam giác ABC có ba đường phân giác AD, BE, CF.

 Chứng minh = 1

Trả lời rút gọn: 

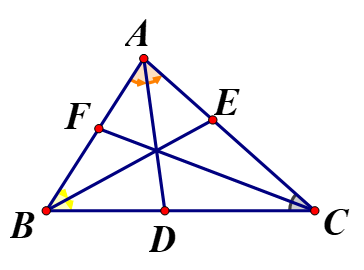
Xét có là các đường phân giác nên ; ;

Ta có: (đpcm)

Luyện tập 4 (Trang 68):

Cho tam giác ABC, điểm D thuộc cạnh BC sao cho . Chứng minh AD là tia phân giác của góc BAC. 

Trả lời rút gọn:

Lấy thuộc sao cho

Theo hệ quả định lí Thalès, có:

Mà nên =>

Khi đó cân tại =>

Mà nên =>

Vậy là phân giác của góc .

BÀI TẬP CUỐI SGK

Bài 1 (Trang 69): Cho tam giác ABC có ba đường phân giác AD, BE, CF. Biết AB = 4, BC = 5, CA = 6. Tính BD, CE, AF.

Trả lời rút gọn:

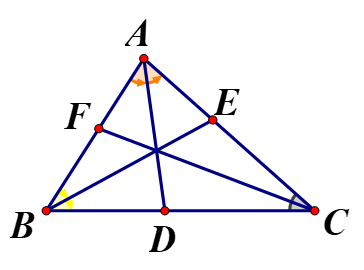
Xét có là đường phân giác nên ; ;

+)  

+)

Từ   Suy ra 

Vậy

+)

Từ  Suy ra 

Vậy

Bài 2 (Trang 69):  

Cho tam giác ABC có đường trung tuyến AM. Tia phân giác của góc ABC lần lượt cắt các đoạn thẳng AM, AC tại điểm D, E. Chứng minh

Trả lời rút gọn: 

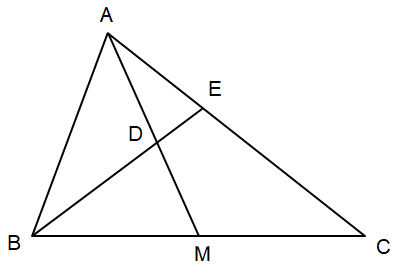
có là đường phân giác nên

là trung điểm của ( là đường trung tuyến) nên

=> (1)

có là phân giác nên (2)

Từ (1)(2) suy ra :

Bài 3 (Trang 69): 

Quan sát Hình 43 và chứng minh =

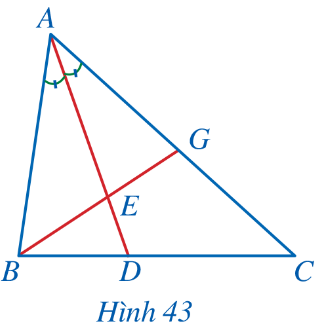
Trả lời rút gọn:

Tam giác ABC có AD là đường phân giác nên

Tam giác ABG có AE là đường phân giác nên =

: =  

Bài 4 (Trang 69): 

Cho hình thoi ABCD (Hình 44). Điểm M thuộc cạnh AB thỏa mãn AB = 3AM. Hai đoạn thẳng AC và DM cắt nhau tại N. Chứng minh ND = 3MN. 

Trả lời rút gọn:

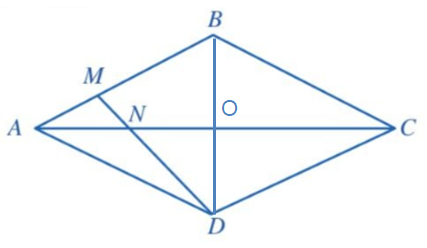
Gọi

Vì là hình thoi nên tại

cân tại có là đường cao nên cũng là đường phân giác

có là đường phân giác => (1)

Ta có : mà => (2)

Từ (1)(2) suy ra hay  

Do đó

Bài 5 (Trang 69):

Cho tam giác ABC vuông tại A có AB = 3, AC = 4, AD là đường phân giác. Tính: 

a) Độ dài các đoạn thẳng BC, DB, DC;

b) Khoảng cách từ điểm D đến đường thẳng AC;

c) Độ dài đường phân giác AD. 

Trả lời rút gọn: 

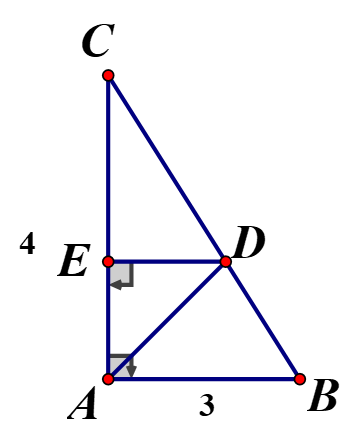
a) + Áp dụng định lí Pythagore trong : BC = 5 cm 

    + Áp dụng tính chất đường phân giác trong , ta có :

    + DC = BC – DB 

          hay => DB = ; DC =

b) Gọi là chân đường vuông góc kẻ từ đến  

Nên khoảng cách từ đến là

Ta có (quan hệ từ song song đến vuông góc)

Suy ra:  =>  =>  

Vậy khoảng cách từ đến là  

c) Xét có nên (định lí Thalès) => =>

vuông tại nên ta có :

Bài 6 (Trang 69): 

Cho tứ giác ABCD với các tia phân giác của các góc CAD và CBD cùng đi qua điểm E thuộc cạnh CD (Hình 45). Chứng minh AD.BC = AC.BD. 

Trả lời rút gọn:

Tam giác ACD có AE là đường phân giác của góc CAD =>

Tam giác BCD có BE là đường phân giác của góc CBD =>

=>  hay (đpcm)