Slide bài giảng toán 8 cánh diều bài 1: Định lí Pythagore

Tóm lược nội dung

CHƯƠNG V. ĐỊNH LÍ PYTHAGORE. TỨ GIÁC

BÀI 1. ĐỊNH LÍ PYTHAGORE (2 tiết)

I. Định lí Pythagore.

Hoạt động 1 (Trang 94): 

Thực hiện các hoạt động sau:

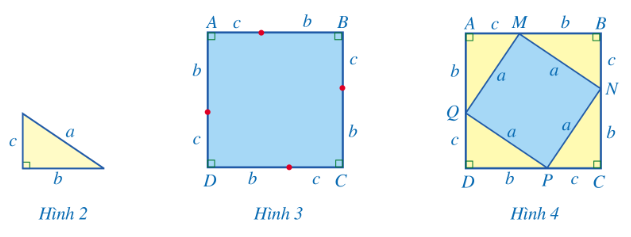
a) Vẽ và cắt giấy để có 4 hình tam giác vuông như nhau với độ dài cạnh huyền là a, độ dài hai cạnh góc vuông là b và c, trong đó a, b, c có cùng đơn vị độ dài (Hình 2).

b. Vẽ hình vuông ABCD có cạnh là b + c như  Hình 3. Đặt 4 hình tam giác vuông đã cắt ở câu a lên hình vuông ABCD vừa vẽ, phần chưa bị che đi là hình vuông MNPQ với độ đài cạnh là a (Hình 4).

c. Gọi S1 là diện tích của hình vuông ABCD. Gọi S2 là tổng diện tích của hình vuông MNPQ và diện tích của 4 tam giác vuông AQM, BMN, CNP, DPQ. So sánh S1 và S2

d. Dựa vào kết quả ở câu c, dự đoán mối liên hệ giữa a² và b²+c²

Trả lời rút gọn:

a), b) HS tự thực hành theo hướng dẫn SGK.

c) là: (đơn vị diện tích).

là: (đơn vị diện tích).

là: (đơn vị diện tích).

Tổng diện tích của 4 tam giác vuông

là:

(đơn vị diện tích).

d) bằng tổng diện tích của hình vuông và diện tích của 4 tam giác vuông hay .

Do đó:

Hay

=>

Luyện tập 1 (Trang 95): 

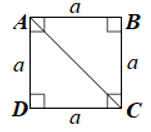
Tính độ dài đường chéo của hình vuông có độ dài cạnh là a.

Trả lời rút gọn:

Ta có hình vuông độ dài các cạnh là . Đường chéo

Áp dụng định lí Pythagore cho vuông tại , có:

=>

II. Định lí Pythagore đảo.

Hoạt động 2 (Trang 95): 

Thực hiện các hoạt động sau:

a) Vẽ một tam giác ABC có AB = 3 cm, AC = 4 cm và BC = 5 cm:

b) Tính và so sánh diện tích của hình vuông có cạnh BC với tổng diện tích của hai hình vuông tương ứng có cạnh AB và AC (Hình 6):

c) Kiểm tra xem góc A của tam giác ABC có phải là góc vuông hay không.

Trả lời rút gọn:

a) 

b) Diện tích của hình vuông có cạnh là:

Diện tích của hình vuông có cạnh là:

Tổng diện tích của hai hình vuông trên là:

Diện tích của hình vuông có cạnh là:

Vậy diện tích của hình vuông có cạnh bằng tổng diện tích của hai hình vuông tương ứng có cạnh và .

c) Dùng thước êke (hoặc thước đo góc) ta xác định được của là góc vuông.

Luyện tập 2 (Trang 96): 

Tam giác có ba cạnh là 20 cm, 21 cm, 29 cm có phải là tam giác vuông hay không?

Trả lời rút gọn:

Ta có: cm

=> Tam giác có ba cạnh là tam giác vuông.

III. Bài tập

Bài 1 (Trang 96): 

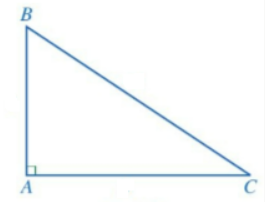
Cho tam giác ABC vuông tại A. Tìm độ dài cạnh còn lại trong mỗi trường hợp sau:

a) AB = 8 cm, BC = 17 cm;

b) AB = 20 cm, AC = 21 cm;

c) AB = AC = 6cm.

Trả lời rút gọn:

Vì vuông tại , nên theo định lí Pythagore ta có :

a) Với

=> => =>

b) Với

=> =>

c) Với

=> =>

Bài 2 (Trang 96): 

Tam giác có độ dài ba cạnh trong mỗi trường hợp sau có phái là tam giác vuông hay không?

a) 12 cm, 35 cm, 37 cm;           

b) 10 cm, 7 cm, 8 cm;                   

c) 11 cm, 6 cm, 7 cm.

Trả lời rút gọn:

a) Ta có : => Đây là 3 cạnh của một tam giác vuông.

b) Ta có :  

=> Đây không phải là 3 cạnh của một tam giác vuông.

c) Ta có :

=> Đây không phải là 3 cạnh của một tam giác vuông.

Bài 3 (Trang 97): 

Cho tam giác vuông cân có độ dài cạnh góc vuông bằng 1 dm. Tính độ dài cạnh huyền của tam giác đó.

Trả lời rút gọn:

Gọi cạnh huyền có độ dài bằng .

Sử dụng định lí Pythagore ta có : .

Bài 4 (Trang 97): 

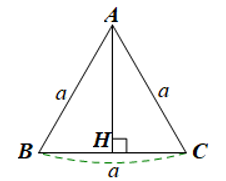
Cho một tam giác đều cạnh a.

a) Tính độ dài đường cao của tam giác đó theo a.

b) Tính diện tích của tam giác đó theo a.

Trả lời rút gọn:

a) Xét có ; Gọi là đường cao của

=> cũng là đường trung tuyến =>

Áp dụng định lí Pythagore vào ta có :

hay => =>

b) (đvdt).

Bài 5 (Trang 97): 

Hình 9 mô tả một thanh gỗ dài 2,6 m dựa vào một bức tường thẳng đứng. Chân thanh gỗ cách mép tường một khoảng là 1 m. Khoảng cách từ điểm thanh gỗ chạm vào tường đến mặt đất là bao nhiêu mét?

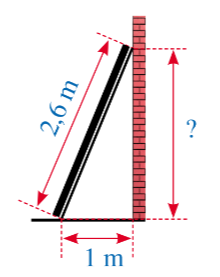
Trả lời rút gọn:

Ta thấy, bức tường thẳng đứng  => góc giữa bức tường với mặt đất bằng

Gọi độ dài từ điểm thanh gỗ chạm vào tường đến mặt đất là (m).

Áp dụng định lí Pythagore ta có : => => (m).

Bài 6 (Trang 97): 

Hình 10 mô tả mặt cắt đứng của một sân khấu ngoài trời có mái che. Chiểu cao của khung phía trước khoảng 7 m, chiểu cao của khung phía sau là 6 m, hai khung cách nhau một khoảng là 5 m. Chiều dài của mái che sân khấu đó là bao nhiêu mét (làm tròn kết quả đến hàng phần trăm)?

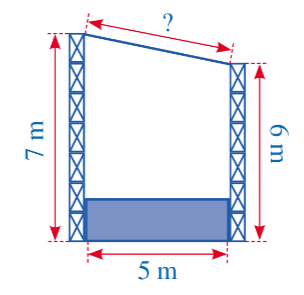
Trả lời rút gọn:

Ta phác họa lại hình hành của mặt cắt đứng của một sân khấu ngoài trời như sau

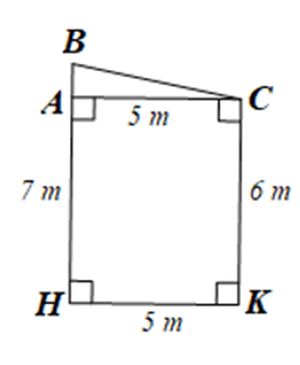
+ Ta có tứ giác là hình chữ nhật => ;

=>

Xét vuông tại có :

Áp dụng định lí Pythagore ta có :  

=> .