Slide bài giảng toán 8 cánh diều bài 3: Đường trung bình của tam giác

Tóm lược nội dung

BÀI 3. ĐƯỜNG TRUNG BÌNH CỦA TAM GIÁC

I. ĐỊNH NGHĨA

Hoạt động 1 (Trang 62):

Quan sát tam giác ABC ở Hình 29 và cho biết hai đầu mút D, E của đoạn thẳng DE có đặc điểm gì. 

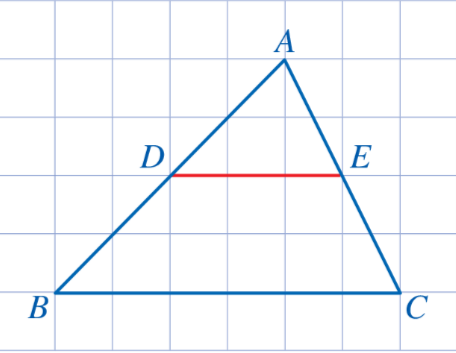
Trả lời rút gọn:

Đầu mút D là trung điểm của đoạn thẳng AB, đầu mút E là trung điểm của đoạn thẳng AC. 

Luyện tập 1 (Trang 62): 

Vẽ tam giác ABC và các đường trung bình của tam giác đó.

Trả lời rút gọn: 

Gọi M, N, H lần lượt là trung điểm của AB, AC, BC.

Do đó: MN, MH, NH là đường trung bình của tam giác ABC.

II. TÍNH CHẤT

Hoạt động 2 (Trang 63):

Cho tam giác ABC có MN là đường trung bình (Hình 31).

a) MN có song song với BC hay không? Vì sao?

b) Tỉ số bằng bao nhiêu?

Trả lời rút gọn:

a) Áp dụng định lý Thales đảo vào ta có: 

nên

b) Theo hệ quả của định lý Thales ta có:   

Luyện tập 2 (Trang 64):

Cho hình thang ABCD (AB // CD). Giả sử M, N, P lần lượt là trung điểm của các đoạn thẳng AD, BC, AC. Chứng minh:

a) M, N, P thẳng hàng.

b) MN= (AB+CD).

Trả lời rút gọn:

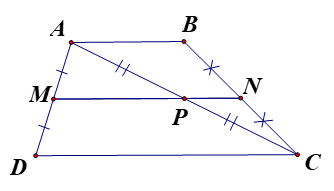
a) + Xét , ta có: là đường trung bình của .

=> và  

+ Xét , ta có: là đường trung bình của .

=> và (2)

Mà AB // CD nên theo Tiên đề Ơclit ta có M, N, P  thẳng hàng.

b) Từ (1) và (2) suy ra 

MN = MP + PN (AB + CD)

BÀI TẬP CUỐI SGK

Bài 1 (Trang 65):

Cho tam giác ABC có M là trung điểm của AB, điểm N thuộc cạnh AC thỏa mãn MN // BC. Chứng minh NA = NC và MN = BC.

Trả lời rút gọn:

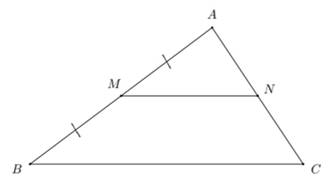
Do nên theo định lý Thales ta có:  

=> là trung điểm của hay

Theo định lý Thales ta có:  =>

Bài 2 (Trang 65): 

Cho tam giác ABC có AM là đường trung tuyến, các điểm N, P phân biệt thuộc cạnh AB sao cho AP = PN = NB. Gọi Q là giao điểm của AM và CP. Chứng minh:

a) MN // CP                     b) AQ = QM                              c) CP = 4PQ.

Trả lời rút gọn: 

a) Ta có => là trung điểm của

Mà là đường trung tuyến => là trung điểm của

=> là đường trung bình của => .

b) Theo câu a) ta có  =>

Mà là trung điểm của nên suy ra là trung điểm của hay .

c) Ta có MN là đường trung bình của => .

là đường trung bình của => =>

Bài 3 (Trang 65): 

Cho tứ giác ABCD có M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. 

a) Chứng minh tứ giác MNPQ là hình bình hành.

b) Cho AC = BD. Chứng minh tứ giác MNPQ là hình thoi.

c) Cho AC ⊥ BD. Chứng minh tứ giác MNPQ là hình chữ nhật.

Trả lời rút gọn:

a) Xét có lần lượt là trung điểm của và

=> là đường trung bình của .

=> và (1)

Xét có lần lượt là trung điểm của và .

=> là đường trung bình của .

=> và (2)

Từ (1) và (2) => MN // PQ và MN = QP 

=> là hình bình hành.

b) Do MQPN nên MQ = NP 

Xét có lần lượt là trung điểm của và .

=> là đường trung bình của .

=> và . 

Mà nên . Suy ra là hình thoi.

c) Ta có => . Do đó tứ giác là hình chữ nhật.

Bài 4 (Trang 65): 

Cho tam giác ABC nhọn có H là trực tâm. Gọi M, N, P, Q lần lượt là trung điểm của các đoạn thẳng AB, BH, HC, CA. Chứng minh tứ giác MNPQ là hình chữ nhật.

Trả lời rút gọn:

Tam giác ABH có: M, N lần lượt là trung điểm của AB, BH.

Suy ra: MN là đường trung bình nên MN // AH và MN = AH (1)

Tam giác ACH có: P, Q lần lượt là trung điểm của CH, AC.

Suy ra: PQ là đường trung bình nên PQ // AH và PQ = AH (2)

Từ (1)(2) suy ra: MN // PQ và MN = PQ. 

Do đó: MNPQ là hình bình hành (3)

Ta có: MN // AH 

Mà AH ⊥ BC (H là trực tâm tam giác ABC)

Suy ra: MN ⊥ BC

Mà MQ // BC (MQ là đường trung bình của tam giác ABC)

Do đó: MN ⊥ MQ (4)

Từ (3)(4) suy ra: MNPQ là hình chữ nhật.

Bài 5 (Trang 65): 

Trong Hình 36, ba cạnh màu vàng AB, BC, CA gợi nên hình ảnh tam giác ABC và đoạn thẳng màu xanh MN là một đường trung bình của tam giác đó. Bạn Duyên đứng ở phía dưới đo khoảng cách giữa hai chân cột số 1 và số 2, từ đó ước lượng được độ dài đoạn thẳng MN khoảng 4,5 m. Khoảng cách giữa hai mép dưới của mái được tính bằng độ dài đoạn thẳng BC. Hỏi khoảng cách đó khoảng bao nhiêu mét?

Trả lời rút gọn:

MN là đường trung bình của tam giác ABC nên MN = BC hay BC = 2MN

Mà khoảng cách giữa hai mép dưới của mái được tính bằng độ dài đoạn thẳng BC

Suy ra: Khoảng cách đó bằng 2.MN = 2.4,5 = 9 m.