Soạn giáo án điện tử Toán 7 Kết nối bài: Luyện tập chung trang 85
Giáo án powerpoint toán 7 kết nối tri thức mới bài bài: Luyện tập chung trang 85. Giáo án soạn theo tiêu chí hiện đại, đẹp mắt với nhiều hình ảnh, nội dung, hoạt động phong phú, sáng tạo. Giáo án điện tử này dùng để giảng dạy online hoặc trình chiếu. Tin rằng, bộ bài giảng này sẽ hỗ trợ tốt việc giảng dạy và đem đến sự hài lòng với thầy cô.









Còn nữa....Giáo án khi tải về là bản đầy đủ. Có full siles bài giảng!
Nội dung giáo án
CHÀO MỪNG CÁC EM ĐẾN VỚI LỚP HỌC
KHỞI ĐỘNG
Câu 1: Chọn câu trả lời đúng. Điền dấu X vào ô trống
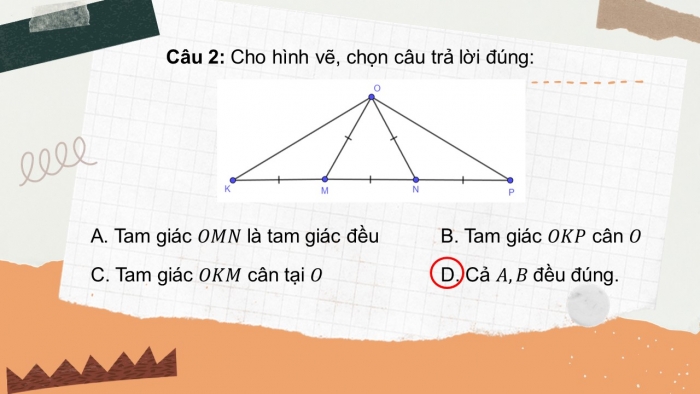
Câu 2: Cho hình vẽ, chọn câu trả lời đúng:
- Tam giác là tam giác đều B. Tam giác cân
- Tam giác cân tại D. Cả đều đúng.
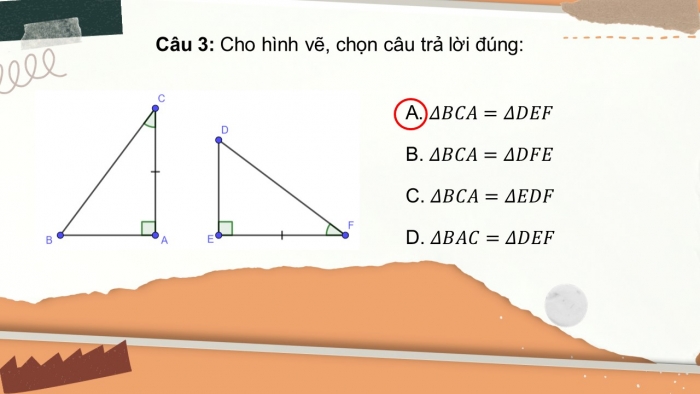
Câu 3: Cho hình vẽ, chọn câu trả lời đúng:
Câu 4: Cho tam giác cân tại , tam giác cân tại và là trung điểm của , chọn câu trả lời đúng:
- thuộc đường trung trực của .
- thuộc đường trung trực của .
- thuộc cùng một đường thẳng.
- đều đúng.
Câu 5: Cho tam giác vuông cân tại , là tia phân giác của góc ( nằm trên ), chọn câu trả lời đúng:
- B.
- D. đều đúng.
LUYỆN TẬP CHUNG
Ví dụ 1
Cho Hình 4.71, biết , .
Gọi lần lượt là trung điểm của các đoạn thẳng . Chứng minh rằng
- a) b) .
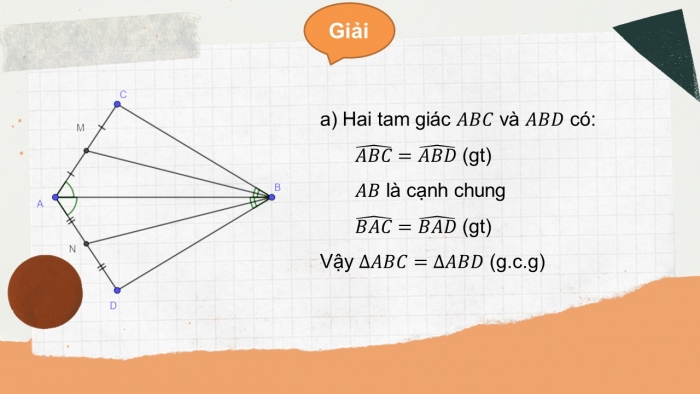
Giải
- a) Hai tam giác và có:
(gt)
là cạnh chung
(gt)
Vậy (g.c.g)
- b) Vì nên , và .
Do lần lượt thuộc nên , .
Vì vậy .
Mặt khác, vì và lần lượt là trung điểm của và nên .
Xét và có:
, ,
Do đó .
Ví dụ 2
Cho là đường trung trực của đoạn thẳng và là giao điểm của với . Cho và là hai điểm phân biệt nằm trên sao cho . Chứng minh rằng
- a) b)
- c) Tam giác cân tại .
Giải
Vì là đường trung trực của đoạn thẳng nên vuông góc với tại .
- a) Xét hai tam giác vuông và có:
là cạnh chung; ( )
Do đó (cạnh huyền – cạnh góc vuông).
- b) Xét hai tam giác và có:
(do )
(do )
là cạnh chung
Vậy (c.c.c)
Do đó (hai góc tương ứng)
- c) Xét hai tam giác vuông và có:
(gt)
là cạnh chung
Do đó (hai cạnh góc vuông)
Vậy (hai cạnh tương ứng)
Suy ra tam giác cân tại .
LUYỆN TẬP – VẬN DỤNG
Bài 4.29 (SGK – tr.86) Cho Hìn 4.73 Hãy tìm số đo của các góc và độ dài của các đoạn thẳng trên hình vẽ.
Giáo án điện tử toán 7 kết nối tri thức, giáo án powerpoint toán 7 KNTT bài: Luyện tập chung trang 85, bài giảng điện tử toán 7 Kết nối
Nâng cấp lên tài khoản VIP để tải tài liệu và dùng thêm được nhiều tiện ích khác
Xem thêm giáo án khác
Bài tập 4.29 trang 86 toán 7 tập 1 KNTT
Cho Hình 4.73. Hãy tính các độ dài a, b và số đo x, y của các góc trên hình vẽ.

Hướng dẫn giải:
Dựa vào định lý tổng ba góc trong một tam giác bằng $180^{\circ}$. Ta suy ra :
Trong tam giác ABD :
x= $180^{\circ}$ -$60^{\circ}$ -$75^{\circ}$ = $45^{\circ}$
Trong tam giác ABC :
y= $180^{\circ}$ -$45^{\circ}$ -$75^{\circ}$ = $60^{\circ}$
Giờ xét 2 tam giác : ABC và ABD , ta có :
- $\widehat{CAB}$ = $\widehat{DAB}$ = $45^{\circ}$
- AB chung
- $\widehat{ABC}$ = $\widehat{ABD}$ = $60^{\circ}$
=> $\Delta$ABC = $\Delta$ABD
Suy ra :
- a= BC = BD = 3,3 cm
- b= AD= AC = 4 cm
Bài tập 4.30 trang 86 toán 7 tập 1 KNTT
Cho góc xOy. Trên tia Ox lấy hai điểm A, M; trên tia Oy lấy hai điểm B, N sao cho OA = OB, OM =ON, OA > OM. Chứng minh rằng:
a. ΔOAN = ΔOBM;
b. ΔAMN = ΔBNM.
Hướng dẫn giải:
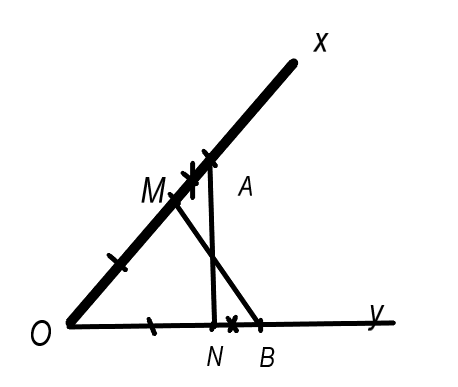
a. Xét ΔOAN và ΔOBM, ta có :
- OA= OB
- Góc O chung
- OM= ON
=> ΔOAN = ΔOBM (c-g-c)
b. Từ câu a => AN= BM. Mà OA = OB=> AM =BN
Xét ΔAMN và ΔBNM, ta có :
- AN= BM
- AM =BN
- MN chung
=> ΔAMN = ΔBNM (c-c-c)
Bài tập 4.31 trang 86 toán 7 tập 1 KNTT
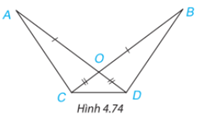
Cho Hình 4.74, biết OA = OB, OC = OD. Chứng minh rằng:
a. AC = BD;
b. ΔACD = ΔBDC.
Hướng dẫn giải:
a. Vì $\widehat{AOC}$ và $\widehat{AOC}$ đối đỉnh nhau => $\widehat{AOC}$ = $\widehat{AOC}$
Xét ΔAOC và ΔBOD, ta có :
- AO = BO
- $\widehat{AOC}$ = $\widehat{AOC}$
- OC= OD
=> ΔAOC = ΔBOD
=> AC = BD
b. Từ giả thiết ta có :
OA + OD= OB +OC => AD = BC
Xét 2 tám giác ΔACD và ΔBDC, ta có :
- AD = BC
- AC = BD
- CD chung
=> ΔACD = ΔBDC (c-c-c)
Bài tập 4.32 trang 86 toán 7 tập 1 KNTT
Cho tam giác MBC vuông tại M có $\widehat{B}=60 ^{\circ}$. Gọi A là điểm nằm trên tia đối của tia MB sao cho MA = MB. Chứng minh rằng tam giác ABC là tam giác đều.
Hướng dẫn giải:
Xét 2 tam giác vuông CMB và CMA có:
- MC chung
- MB=MA
=>ΔCMB=ΔCMA (c.g.c)
=>CA = CB (2 cạnh tương ứng).
=> Tam giác ABC cân tại C.
Mà góc B bằng $\widehat{B}=60 ^{\circ}$
=>Tam giác ABC đều.
