Soạn giáo án điện tử Toán 7 Kết nối bài: Luyện tập chung trang 10
Giáo án powerpoint toán 7 kết nối tri thức mới bài bài: Luyện tập chung trang 10. Giáo án soạn theo tiêu chí hiện đại, đẹp mắt với nhiều hình ảnh, nội dung, hoạt động phong phú, sáng tạo. Giáo án điện tử này dùng để giảng dạy online hoặc trình chiếu. Tin rằng, bộ bài giảng này sẽ hỗ trợ tốt việc giảng dạy và đem đến sự hài lòng với thầy cô.







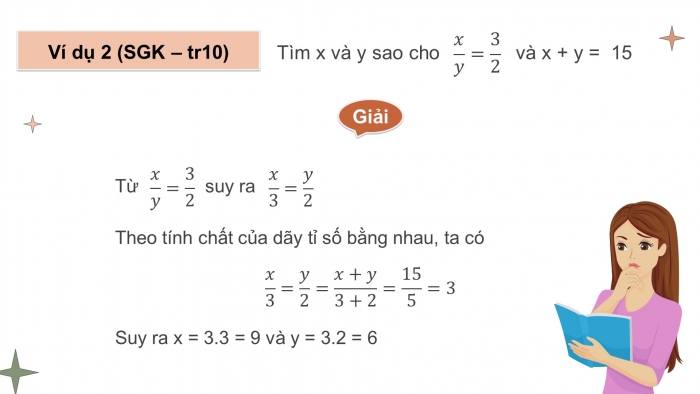




Còn nữa....Giáo án khi tải về là bản đầy đủ. Có full siles bài giảng!
Nội dung giáo án
BÀI LUYỆN TẬP CHUNG TRANG 10 (2 TIẾT)
- KHỞI ĐỘNG
- Em hãy nêu lại các tính chất của tỉ lệ thức.
- Em hãy nêu lại tính chất của dãy tỉ số bằng nhau.
- NỘI DUNG BÀI HỌC
Các dạng toán:
Dạng 1: Lập các tỉ lệ thức
Dạng 2: Tìm hai số biết tổng (hoặc hiệu) và tỉ số của chúng.
Dạng 3: Bài toán có lời văn
III. PHẦN TRIỂN KHAI KIẾN THỨC
HĐ: PHÂN TÍCH CÁC VÍ DỤ:
GV giới thiệu các dạng toán HS cần nắm được:
Dạng 1: Lập các tỉ lệ thức (Ví dụ 1)
Dạng 2: Tìm hai số biết tổng (hoặc hiệu) và tỉ số của chúng. (Ví dụ 2)
Dạng 3: Bài toán có lời văn (Ví dụ 3)
HS đọc, nêu phương pháp giải, hoàn thành Ví dụ 1
Ví dụ 1 (SGK-tr10): Lập các tỉ lệ thức có thể được từ bốn số: 15; 18; 20; 2
Giải:
Từ bốn số đã cho ta lập được đẳng thức: 15.24 = 18.20 (vì đều bằng 360)
Từ đẳng thức này ta lập được bốn tỉ lệ thức sau:
; ; ;
GV hướng dẫn PP giải, HS đọc, tự trình bày Ví dụ 2, sau đó trao đổi nhóm đôi kiểm tra chéo.
Ví dụ 2 (SGK-tr10): Tìm x và y sao cho và x + y = 15
Giải:
Từ suy ra
Theo tính chất của dãy tỉ số bằng nhau, ta có:
Suy ra x = 3.3 = 9 và y = 3.2 = 6
GV hướng dẫn PP giải, HS đọc, tự trình bày Ví dụ 3, sau đó trao đổi nhóm đôi kiểm tra chéo.
Ví dụ 3 (SGK-tr10). Tính độ dài các cạnh của một tam giác, biết độ dài các cạnh của nó tỉ lệ với 2; 3; 4 và cạnh lớn nhất dài hơn cạnh nhỏ nhất 6 cm.
GV đặt câu hỏi dẫn dắt:
Gọi độ dài các cạnh của một tam giác lần lượt là x, y, z. Độ dài các cạnh của nó tỉ lệ với 2; 3; 4, thì ta suy ra được điều gì? Cạnh lớn nhất dài hơn cạnh nhỏ nhất 6 cm, ta suy ra được biểu thức nào?
Giải:
Gọi độ dài ba cạnh của tam giác (theo thứ tự từ nhỏ đến lớn) lần lượt là: x, y, z (cm, x, y, z> 0)
Theo đề bài, ta có: và z – x = 6
Theo tính chất của dãy tỉ số bằng nhau, ta có:
Suy ra x = 3.2 = 6; y = 3.3 = 9 và z = 3.4 = 12
Vậy độ dài ba cạnh của tam giác đó là 6cm, 9 cm và 12 cm.
- LUYỆN TẬP
HOẠT ĐỘNG NHÓM ĐÔI: hoàn thành BT6.11; 6.12; 6.13; 6.16 (SGK)
Bài 6.11 (Tr10)
Lập các tỉ lệ thức có thể được từ đẳng thức 3x = 4y (x.y ≠ 0).
Giải:
Từ đẳng thức , ta có thể lập được bốn tỉ lệ thức sau:
; ; ;
Bài 6.12 (Tr10)
Hãy lập tất cả các tỉ lệ thức có thể được từ bốn số: 5; 10; 25; 50.
Giải:
Từ 4 số trên, ta chỉ có đẳng thức: 5 . 50 = 10 . 25 (vì đều bằng 250)
Từ đẳng thức trên, có thể lập được các tỉ lệ thức là:
; ; ;
Bài 6.13 (Tr10). Tìm x và y, biết:
- a) và x+y=16
- b) và x−y=−15
Giải:
- a) Từ suy ra
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
Từ đây tính được: x = 2 . 5 = 10 và y = 2 . 3 = 6
- b) Từ suy ra 4x = 9y
Từ đẳng thức này ta suy ra tỉ lệ thức:
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
Từ đây tính được: x = -3 . 9 = -27 và y = -3 . 4 = -12
Bài 6.16 (Tr10). Tìm ba số x, y, z, biết rằng: và x+2y−3z = −12
Giáo án điện tử toán 7 kết nối tri thức, giáo án powerpoint toán 7 KNTT bài: Luyện tập chung trang 10, bài giảng điện tử toán 7 Kết nối
Nâng cấp lên tài khoản VIP để tải tài liệu và dùng thêm được nhiều tiện ích khác
Xem thêm giáo án khác
Bài tập 6.11 trang 10 toán 7 tập 2 KNTT
Lập các tỉ lệ thức có thể được từ đẳng thức 3x = 4y (x.y $\neq $ 0).
Hướng dẫn giải:
Từ đẳng thức $3x = 4y$, ta có thể lập được bốn tỉ lệ thức sau:
$\frac{3}{4} = \frac{y}{x}$; $\frac{3}{y} = \frac{4}{x}$; $\frac{x}{-4} = \frac{y}{3}$; $\frac{x}{y} = \frac{4}{3}$
Bài tập 6.12 trang 10 toán 7 tập 2 KNTT
Hãy lập tất cả các tỉ lệ thức có thể được từ bốn số: 5; 10; 25; 50.
Hướng dẫn giải:
Từ 4 số trên, ta chỉ có đẳng thức: 5 . 50 = 10 . 25 (vì đều bằng 250)
Từ đẳng thức trên, có thể lập được các tỉ lệ thức là:
$\frac{5}{25} = \frac{10}{50}$; $\frac{5}{25} = \frac{10}{50}$; $\frac{50}{10} = \frac{25}{5}$; $\frac{50}{25} = \frac{10}{5}$
Bài tập 6.13 trang 10 toán 7 tập 2 KNTT
Tìm $x$ và $y$, biết:
a) $\frac{x}{y} = \frac{5}{3}$ và $x + y = 16$
b) $\frac{x}{y} = \frac{9}{4}$ và $x - y = -15$
Hướng dẫn giải:
a) Từ $\frac{x}{y} = \frac{5}{3}$ suy ra 3x = 5y
Từ đẳng thức này ta suy ra tỉ lệ thức: $\frac{x}{5} = \frac{y}{3}$
Theo tính chất của tỉ lệ thức, ta có:
$\frac{x}{5} = \frac{y}{3} = \frac{x + y}{5+3} = \frac{x+y}{8} = \frac{16}{8} = 2$
=> Từ đây tính được: x = 2 . 5 = 10 và y = 2 . 3 = 6
b) Từ $\frac{x}{y} = \frac{9}{4}$ suy ra 4x = 9y
Từ đẳng thức này ta suy ra tỉ lệ thức: $\frac{x}{9} = \frac{y}{4}$
Theo tính chất của tỉ lệ thức, ta có:
$\frac{x}{9} = \frac{y}{4} = \frac{x - y}{9-4} = \frac{x-y}{5} = \frac{-15}{5} = -3$
=> Từ đây tính được: x = -3 . 9 = -27 và y = -3 . 4 = -12
Bài tập 6.14 trang 10 toán 7 tập 2 KNTT
Tỉ số của số học sinh của hai lớp 7A và 7B là 0,95. Hỏi mỗi lớp có bao nhiêu học sinh, biết số học sinh của một lớp nhiều hơn lớp kia là 2 em?
Hướng dẫn giải:
Gọi x, y lần lượt là số học sinh của lớp 7A và 7B.
- Theo đề bài, ta được: $\frac{x}{y} = 0,95 \Leftrightarrow \frac{x}{y} = \frac{19}{20} \Leftrightarrow \frac{x}{19} = \frac{y}{20}$
Như vậy, từ đề bài ta có: $\frac{x}{19} = \frac{y}{20}$ và y - x = 2
- Áp dụng tính chất của tỉ lệ thức, ta có:
$\frac{x}{19} = \frac{y}{20} = \frac{y-x}{20-19} = \frac{y-x}{1} = \frac{2}{1} = 2$
- Từ đây tính được:
- x = 2 . 19 = 38
- y = 2 . 20 = 40
Kết luận:
- Số học sinh của lớp 7A là 38 học sinh.
- Số học sinh của lớp 7B là 40 học sinh.
Bài tập 6.15 trang 10 toán 7 tập 2 KNTT
Người ta định làm một con đường trong 15 ngày. Một đội công nhân 45 người làm trong 10 ngày mới được một nửa công việc. Hỏi phải bổ sung thêm bao nhiêu người nữa để có thể hoàn thành công việc đúng hạn (biết năng suất lao động của mỗi người như nhau).
Hướng dẫn giải:
Gọi: x là số lượng công nhân bổ sung thêm để hoàn thành công việc đúng hạn.
- Thời gian hoàn thành là 15 ngày, đội công nhân làm được 10 ngày.
- Giai đoạn đầu, thời gian và khối lượng công việc đã làm: $\frac{2}{3}$ thời gian và $\frac{1}{2}$ khối lượng công việc.
=> Giai đoạn còn lại, thời gian và khối lượng công việc còn lại lần lược là: $\frac{1}{3}$ và $\frac{1}{2}$
=> Vậy khối lượng công việc là bằng nhau ở hai giai đoạn.
Từ đó, ta có công thức:
$45 . \frac{2}{3} = (x + 45). \frac{1}{3}$
Suy ra: $x = 45$
* Vậy: số lượng công nhân bổ sung thêm để hoàn thành công việc đúng hạn là 45 công nhân.
Bài tập 6.16 trang 10 toán 7 tập 2 KNTT
Tìm ba số $x$, $y$, $z$, biết rằng: $\frac{x}{2} = \frac{y}{3}= \frac{z}{4}$ và $x + 2y -3z = -12$
Hướng dẫn giải:
- Áp dụng tính chất của tỉ lệ thức, ta có:
$\frac{x}{2} = \frac{y}{3} = \frac{z}{4} = \frac{x+2y-3z}{2+2.3-3.4} = \frac{x+2y-3z}{-4} = \frac{-12}{-4} = 3$
=> Từ đây tính được:
- x = 3 . 2 = 6
- y = 3 . 3 = 9
- z = 3 . 4 = 12
