Soạn giáo án điện tử Toán 7 Kết nối bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác
Giáo án powerpoint toán 7 kết nối tri thức mới bài bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác. Giáo án soạn theo tiêu chí hiện đại, đẹp mắt với nhiều hình ảnh, nội dung, hoạt động phong phú, sáng tạo. Giáo án điện tử này dùng để giảng dạy online hoặc trình chiếu. Tin rằng, bộ bài giảng này sẽ hỗ trợ tốt việc giảng dạy và đem đến sự hài lòng với thầy cô.





Còn nữa....Giáo án khi tải về là bản đầy đủ. Có full siles bài giảng!
Nội dung giáo án
CHÀO MỪNG CÁC EM ĐẾN VỚI LỚP HỌC
KHỞI ĐỘNG
Thế nào là hai đoạn thẳng bằng nhau?
Ta nói hai đoạn thẳng bằng nhau nếu chúng có cùng độ dài, hai góc bằng nhau nếu chúng có cùng số đo góc. Vậy hai tam giác như thế nào thì được gọi là bằng nhau và làm thế nào để kiểm tra được hai tam giác đó bằng nhau?
BÀI 13: HAI TAM GIÁC BẰNG NHAU.
TRƯỜNG HỢP BẰNG NHAU THỨ NHẤT CỦA TAM GIÁC
NỘI DUNG BÀI HỌC
Hai tam giác bằng nhau
Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh.
- HAI TAM GIÁC BẰNG NHAU
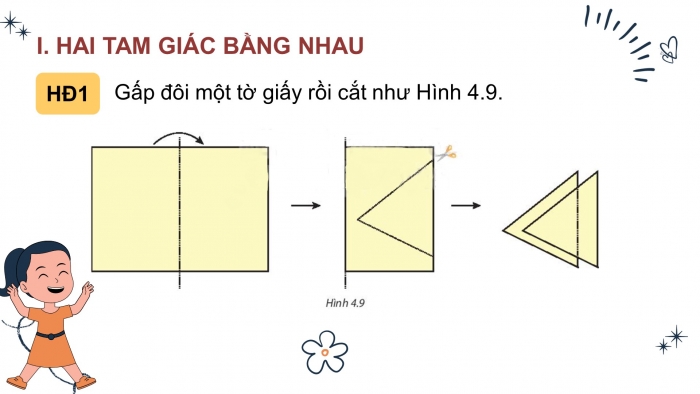
Gấp đôi một tờ giấy rồi cắt như Hình 4.9.
Phần được cắt ra là hai tam giác “chồng khít” lên nhau. Theo em
- Các cạnh tương ứng có bằng nhau không?
- Các góc tương ứng có bằng nhau không?
- Các cạnh tương ứng chồng lên nhau bằng nhau.
- Các góc tương ứng chồng lên nhau thì có số đo bằng nhau.
KẾT LUẬN
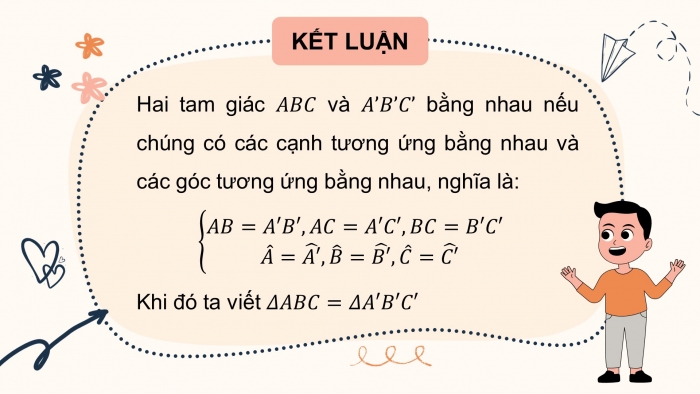
Hai tam giác và bằng nhau nếu chúng có các cạnh tương ứng bằng nhau và các góc tương ứng bằng nhau, nghĩa là:
Khi đó ta viết
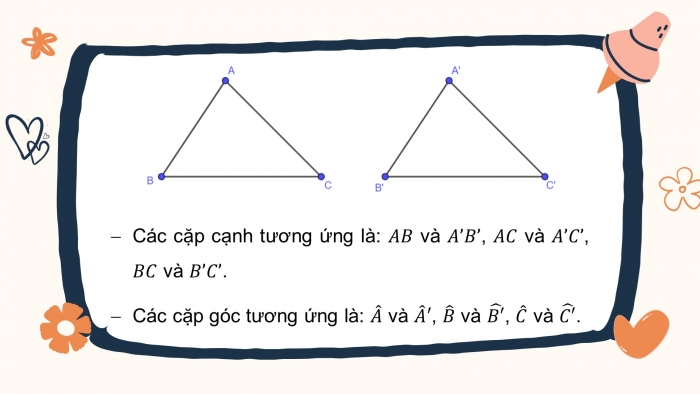
- Các cặp cạnh tương ứng là: và , và , và .
- Các cặp góc tương ứng là: và , và , và .
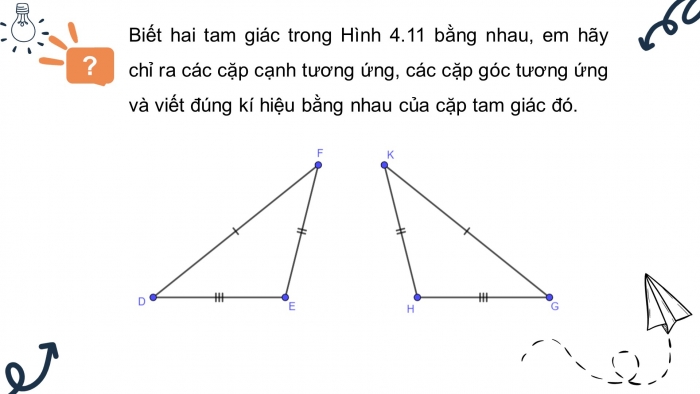
- Biết hai tam giác trong Hình 4.11 bằng nhau, em hãy chỉ ra các cặp cạnh tương ứng, các cặp góc tương ứng và viết đúng kí hiệu bằng nhau của cặp tam giác đó.
Trả lời
- Các cặp cạnh tương ứng: và , và , và
- Các cặp góc tương ứng: và , và , và .
- Kí hiệu: .
Ví dụ 1
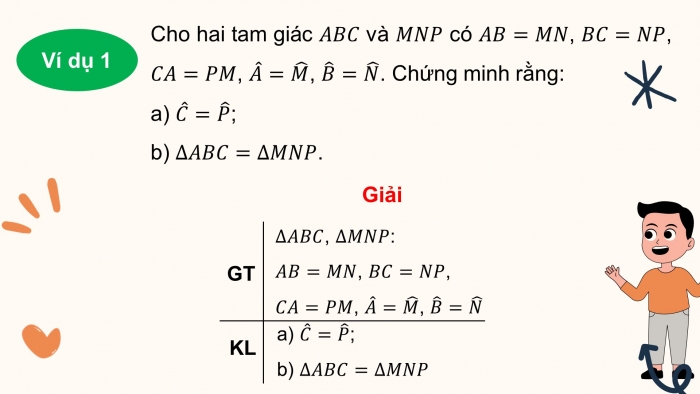
Cho hai tam giác và có , , , , . Chứng minh rằng:
- a) ;
- b) .
Giải
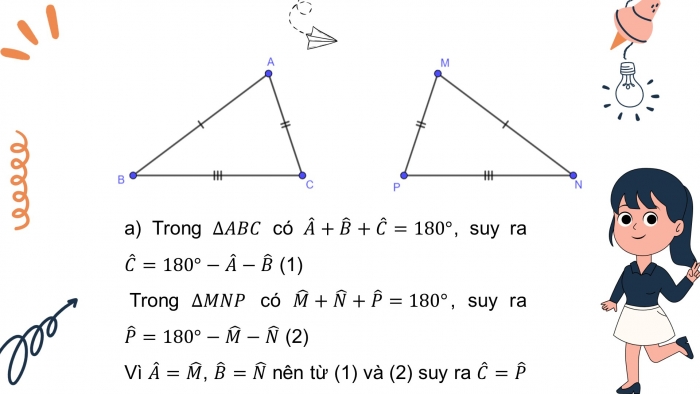
- a) Trong có , suy ra (1)
Trong có , suy ra (2)
Vì , nên từ (1) và (2) suy ra
- b) Hai tam giác và có:
, , ;
, ,
Vậy hai tam giác và có các cạnh và các góc tương ứng bằng nhau.
Do đó .
Luyện tập 1
Cho tam giác bằng tam giác . Biết rằng , , . Hãy tính độ dài đoạn thẳng và số đo góc .
Giải
Vì nên ;
Ta có:
hay .
- TRƯỜNG HỢP BẰNG NHAU THỨ NHẤT CỦA TAM GIÁC: CẠNH – CẠNH – CẠNH (C.C.C)
HĐ2
Vẽ tam giác có , , theo các bước sau:
- Dùng thước thẳng có vạch chia vẽ đoạn thẳng .
- Vẽ cung tròn tâm bán kính và cung tròn tâm bán kính sao cho hai cung tròn cắt nhau tại điểm .
- Vẽ đoạn thẳng ta được tam giác .
Giáo án điện tử toán 7 kết nối tri thức, giáo án powerpoint toán 7 KNTT bài 13: Hai tam giác bằng nhau. Trường, bài giảng điện tử toán 7 Kết nối
Nâng cấp lên tài khoản VIP để tải tài liệu và dùng thêm được nhiều tiện ích khác
Xem thêm giáo án khác
1. HAI TAM GIÁC BẰNG NHAU
Hoạt động 1: Gấp đôi một tờ giấy rồi cắt như Hình 4.9.
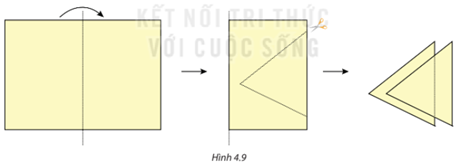
Phần được cắt ra là hai tam giác “chồng khít" lên nhau.Theo em:
- Các cạnh tương ứng có bằng nhau không?
Các góc tương ứng có bằng nhau không?
Hướng dẫn giải:
Từ hình vẽ ta thấy :
Các cạnh tương ứng bằng nhau.
Các góc tương ứng bằng nhau.
Câu hỏi 1: Biết hai tam giác trong Hình 4.11 bằng nhau, em hãy chỉ ra các cặp cạnh tương ứng, các cặp góc tương ứng và viết đúng kí hiệu bằng nhau của cặp tam giác đó.

Hướng dẫn giải:
Các cạnh tương ứng bằng nhau: DE = HG; EF= HK; DF=KG
Các góc tương ứng bằng nhau: $\widehat{E}$ = $\widehat{H}$; $\widehat{F}$ = $\widehat{K}$; $\widehat{D}$ = $\widehat{G}$
Luyện tập 1: Cho tam giác ABC bằng tam giác DEF (H. 4.13). Biết rằng BC = 4 cm, $\widehat{ABC}$= $40^{\circ} $; $\widehat{ACB}$= $60^{\circ} $. Hãy tính độ dài đoạn thẳng EF và số đo góc EDF.
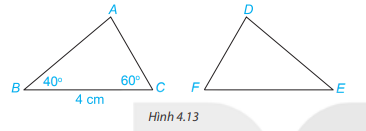
Hướng dẫn giải:
Trong tam giác ABC ta có : $\widehat{BAC}$= $180^{\circ} $ - $40^{\circ} $- $60^{\circ} $ = $80^{\circ} $
Theo đề bài ta có : 2 tam giác ABC và DEF bằng nhau nên suy ra:
2 góc tương ứng $\widehat{BAC}$ và $\widehat{EDF}$ bằng nhau= > $\widehat{EDF}$ = $80^{\circ} $
2 cạnh tương ứng EF= BC = 4cm
2. TRƯỜNG HỢP BẰNG NHAU THỨ NHẤT CỦA TAM GIÁC: CẠNH - CẠNH - CẠNH
Hoạt động 2: Vẽ tam giác ABC có AB=5cm,AC=4cm, BC=6cm theo các bước sau:
- Dùng thước thẳng có vạch chia vẽ đoạn thẳng BC=6cm
Vẽ cung tròn tâm B bán kính 5cm và cung tròn tâm C bán kính 4cm sao cho hai cung tròn cắt nhau tại điểm A(H.4.14)
Vẽ các đoạn thẳng A B, A C ta được tam giác ABC.
Hướng dẫn giải:

Hoạt động 3: Tương tự, vẽ thêm tam giác A′B′C′ có A′B′=5cm,A′C′=4cm,B′C′=6cm
Dùng thước đo góc kiểm tra xem các góc tương ứng của hai tam giác ABC và A′B′C′có bằng nhau không.
Hai tam giác ABC và A′B′C′có bằng nhau không?
Hướng dẫn giải:
Các góc tương ứng của hai tam giác ABC và A′B′C′có bằng nhau .
Hai tam giác ABC và A′B′C′ bằng nhau không?
Câu hỏi: Trong Hình 4.15, những cặp tam giác nào bằng nhau?
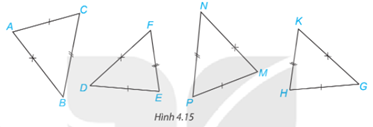
Hướng dẫn giải:
- Xét ΔABC và ΔMNP :
AB = MN; BC = NP; AC=MP
=> ΔABC = ΔMNP
- Xét ΔDEF và ΔGHK
DE=GH; EF=HK; DF=GK
=> ΔDEF=ΔGHK
Luyện tập 2: Cho hình 4.17, biết AB=AD, BC=DC. Chứng minh rằng ΔABC=ΔADC
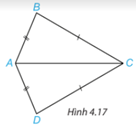
Hướng dẫn giải:
Xét tam giác ΔABC và ΔADC:
AB=AD; BC=DC; AC chung
=> ΔABC=ΔADC
Vận dụng: Người ta dùng compa và thước thẳng để vẽ tia phân giác của góc xOy

1. Vẽ đường tròn tâm O, cắt Ox và Oy lần lượt tại A và B.
2. Vẽ đường tròn tâm A bán kính AO và đường tròn tâm B bán kính BO. Hai đường tròn cắt nhau tại điểm M khác điểm O.
3. Vē tia Oz đi qua M. Em hãy giải thích vì sao tia OM là tia phân giác của góc xOy.
Hướng dẫn giải:
Xét ΔOAM và ΔOBM , ta có :
- OA=OB(=R)
- OM chung
- AM=BM (do hai đường tròn tâm A và B có bán kính bằng nhau)
⇒ ΔOAM = ΔOBM
⇒ 2 góc tương ứng $\widehat{MOB} = \widehat{MOA}$
Mà tia OM nằm trong góc xOy => OM là tia phân giác của góc xOy.
