Soạn giáo án điện tử Toán 7 Kết nối bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác
Giáo án powerpoint toán 7 kết nối tri thức mới bài bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác. Giáo án soạn theo tiêu chí hiện đại, đẹp mắt với nhiều hình ảnh, nội dung, hoạt động phong phú, sáng tạo. Giáo án điện tử này dùng để giảng dạy online hoặc trình chiếu. Tin rằng, bộ bài giảng này sẽ hỗ trợ tốt việc giảng dạy và đem đến sự hài lòng với thầy cô.







Còn nữa....Giáo án khi tải về là bản đầy đủ. Có full siles bài giảng!
Nội dung giáo án
CHÀO MỪNG CÁC EM ĐẾN VỚI BUỔI HỌC
KHỞI ĐỘNG
Em hãy nhắc lại khái niệm hai tam giác bằng nhau và trường hợp bằng nhau thứ nhất của hai tam giác.
BÀI 14: TRƯỜNG HỢP BẰNG NHAU THỨ HAI VÀ THỨ BA CỦA TAM GIÁC
NỘI DUNG BÀI HỌC
Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh.
Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc.
- TRƯỜNG HỢP BẰNG NHAU THỨ HAI CỦA TAM GIÁC: CẠNH – GÓC – CẠNH (C.G.C)
HĐ1
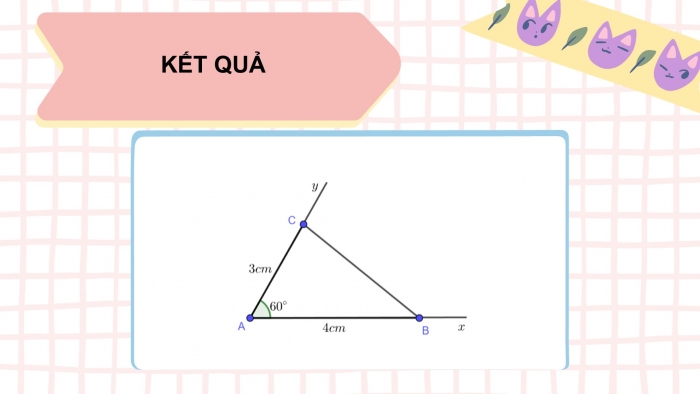
Vẽ . Lấy điểm trên tia và điểm trên tia sao cho: , .
Nối điểm với điểm ta được tam giác .
Dùng thước thẳng có vạch chia đo dộ dài cạnh của tam giác .
KẾT QUẢ
HĐ2
Vẽ thêm tam giác với , và .
Dùng thước thẳng có vạch chia hoặc compa để so sánh độ dài các cạnh tương ứng của hai tam giác và .
- Hai tam giác và có bằng nhau không?
- Độ dài cạnh và của hai tam giác em vừa vẽ có bằng các cạnh và của hai tam giác các bạn khác vẽ không?
- Hai tam giác em vừa vẽ có bằng hai tam giác mà các bạn khác vẽ không?
Trả lời
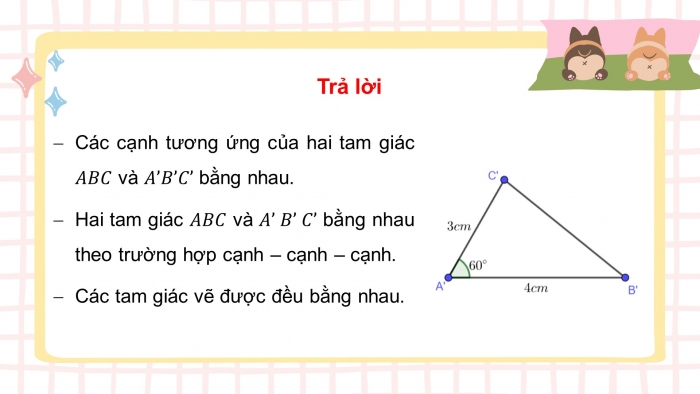
- Các cạnh tương ứng của hai tam giác và bằng nhau.
- Hai tam giác và bằng nhau theo trường hợp cạnh – cạnh – cạnh.
- Các tam giác vẽ được đều bằng nhau.
Chú ý:
Trong tam giác , góc được gọi là góc xen giữa hai cạnh và của tam giác .
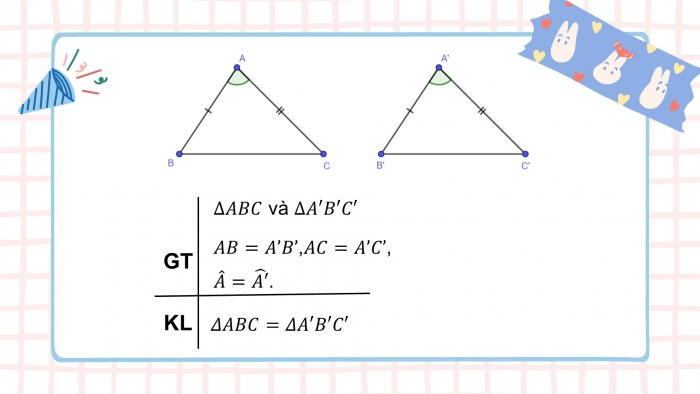
Định lí: Trường hợp bằng nhau cạnh – góc – cạnh (c.g.c)
Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
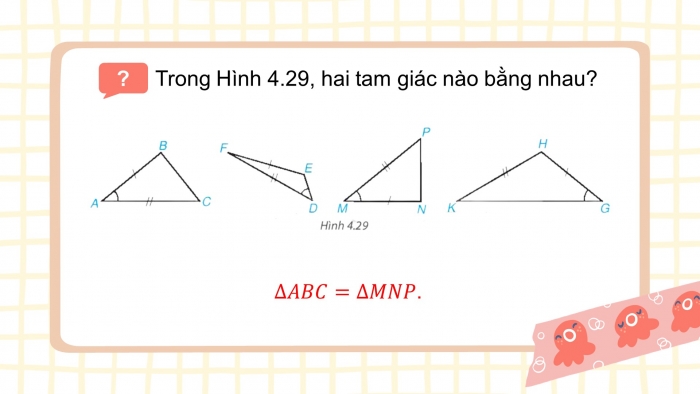
Trong Hình 4.29, hai tam giác nào bằng nhau?
.
Ví dụ 1
Xét hai tam giác và có:
;
;
là cạnh chung
Vậy (c.g.c).
Luyện tập 1
Hai tam giác và trong Hình 4.31 có bằng nhau không? Vì sao?
Giải
+) Xét tam giác có:
.
+ Xét hai tam giác và có:
(c.g.c)
Vận dụng
Cho Hình 4.32, biết , và . Chứng minh rằng:
- a)
- b) .
Giải
- a)
- b) Xét hai tam giác và có:
(cmt)
(c.g.c)
Giáo án điện tử toán 7 kết nối tri thức, giáo án powerpoint toán 7 KNTT bài 14: Trường hợp bằng nhau thứ hai, bài giảng điện tử toán 7 Kết nối
Nâng cấp lên tài khoản VIP để tải tài liệu và dùng thêm được nhiều tiện ích khác
Xem thêm giáo án khác
1. TRƯỜNG HỢP BẰNG NHAU THỨ HAI CỦA TAM GIÁC
Hoạt động 1: Vẽ $\widehat{xAy}=60^{\circ}$ . Lấy điểm B trên tia Ax và điểm C trên tia Ay sao cho: AB = 4 cm, AC = 3 cm. Nối điểm B với điểm C ta được tam giác ABC (H.4.27)
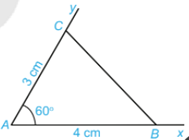
Dùng thước thẳng có vạch chia đo độ dài cạnh BC của tam giác ABC.
Hướng dẫn giải:
Dùng thước thẳng có vạch chia đo độ dài cạnh BC ta được: BC=3,6cm.
Hoạt động 2: Vẽ thêm tam giác A’B’C’ với $\widehat{B'A'C'}=60^{\circ}$, A’B’ = 4 cm và A'C'= 3 cm (H.4.28).

Dùng thước thẳng có vạch chia hoặc compa để so sánh độ dài các cạnh tương ứng của hai tam giác ABC và ABC.
- Hai tam giác ABC và ABC có bằng nhau không?
- Độ dài các cạnh AB và AB của hai tam giác em vừa vẽ có bằng các cạnh AB và AB của hai tam giác các bạn khác về không?
- Hai tam giác em vừa vẽ có bằng hai tam giác mà các bạn khác vẽ không?
Hướng dẫn giải:
- Độ dài các cạnh tương ứng của 2 tam giác ABC và A’B’C’ bằng nhau.
- Hai tam giác ABC và ABC có bằng nhau.
- Độ dài các cạnh AB và AB của hai tam giác em vừa vẽ có bằng các cạnh AB và AB của hai tam giác các bạn khác vẽ.Hai tam giác em vừa vẽ có bằng hai tam giác mà các bạn khác vẽ.
Câu hỏi: Trong Hình 4.29, hai tam giác nào bằng nhau?

Hướng dẫn giải:
Xét 2 tam giác ABC và MNP có:
AB=MN; $\widehat{BAC}$ = $\widehat{NMP}$ ; AC=MP
=> ΔABC=ΔMNP(c.g.c)
Luyện tập 1: Hai tam giác ABC và MNP trong Hình 431 Có bằng nhau không? Vì sao?

Hướng dẫn giải:
Xét tam giác MNP , ta có :
$\widehat{M}$ = $180^{\circ} -50 ^{\circ}- 70^{\circ}$= $60^{\circ}$
Xét 2 tam giác ABC và MNP có :
$\widehat{A}$ = $\widehat{M}$
AC=MP , AB= MN
=> 2 tam giác ABC = MNP (c-g-c)
Vận dụng: Cho Hình 4.32, biết $\widehat{OAB}$ = $\widehat{ODC}$,OA=OD và AB=CD
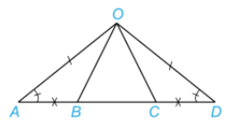
Chứng minh rằng:
a. AC=DB
b. ΔOAC=ΔODB
Hướng dẫn giải:
a. Ta có :
AC= AB+ BC
DB = DC+ CB
Mà AB = DC = > AB+ BC = DC+ CB=> AC= DB
b. Xét ΔOAC và ΔODB, ta có:
OA = OD
$\widehat{A}$= $\widehat{D}$
AC= DB
=> ΔOAC = ΔODB (c-g-c)
2. TRƯỜNG HỢP BẰNG NHAU THỨ BA CỦA TAM GIÁC (GÓC - CẠNH - GÓC)
Hoạt động 3: Vẽ đoạn thẳng BC=3cm. Vẽ hai tia Bx và Cy sao cho $\widehat{xBC}= 80^{\circ} $, $\widehat{yBC}= 40^{\circ} $ như Hình 4.33. Lấy giao điểm A của hai tia Bx và Cy, ta được tam giác ABC (H.4.33)

Dùng thước thẳng có vạch chia độ dài hai cạnh AB, AC của tam giác ABC.
Hướng dẫn giải:
AB=2,2 cm
AC=3,4 cm
Hoạt động 4: Vẽ thêm tam giác A′B′C′ sao cho B′C′=3cm, $\widehat{A'B'C'}= 80^{\circ} $, $\widehat{A'C'B'}= 40^{\circ} $.(H.4.34). Dùng thước thẳng có vạch chia hoặc compa so sánh độ dài các cạnh của hai tam giác ABC và A′B′C′. Hai tam giác ABC và A′B′C′ có bằng nhau không?
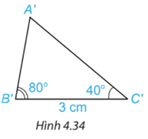
Hướng dẫn giải:
A’B’=2,2 cm
A’C’=3,4 cm
ΔABC = ΔA′B′C′
Câu hỏi: Hai tam giác nào trong Hình 4.35 bằng nhau?
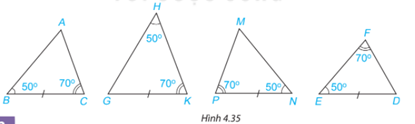
Hướng dẫn giải:
Xét 2 tam giác ABC và MNP, ta có :
$\widehat{B}$= $\widehat{N}$
BC= PN
$\widehat{C}$=$\widehat{P}$
Luyện tập 2: Chứng minh hai tam giác ABD và CBD trong hình 4.37 bằng nhau.
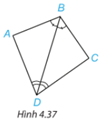
Hướng dẫn giải:
Xét 2 tam giác ABD và CBD ta có :
- $\widehat{ADB}$= $\widehat{CDB}$
- BD chung
- $\widehat{ABD}$= $\widehat{CBD}$
=> ΔABD = ΔCBD
Thử thách nhỏ: Bạn Lan nói rằng: “Nếu tam giác này có một cạnh cùng một góc kề và góc đối diện tương ứng bằng một cạnh cùng một góc kề và góc đối diện của tam giác kia thì hai tam giác đó bằng nhau” (H.4.38). Theo em bạn Lan nói có đúng không? Vì sao?

Hướng dẫn giải:
Bạn Lan nói đúng vì : Áp dụng định lý tổng 3 góc trong một tam giác bằng $180^{\circ}$. Mà 2 trong 3 góc của 2 tam giác là bằng nhau thì góc còn lại cũng bằng nhau.
Tức là : $\widehat{C}$= $\widehat{C'}$
Vậy ΔABC = ΔA'B'C' ( g-c-g)
