Soạn giáo án điện tử Toán 7 Kết nối bài: Bài tập cuối chương I (1 tiết)
Giáo án powerpoint toán 7 kết nối tri thức mới bài bài: Bài tập cuối chương I (1 tiết). Giáo án soạn theo tiêu chí hiện đại, đẹp mắt với nhiều hình ảnh, nội dung, hoạt động phong phú, sáng tạo. Giáo án điện tử này dùng để giảng dạy online hoặc trình chiếu. Tin rằng, bộ bài giảng này sẽ hỗ trợ tốt việc giảng dạy và đem đến sự hài lòng với thầy cô.









Còn nữa....Giáo án khi tải về là bản đầy đủ. Có full siles bài giảng!
Nội dung giáo án
CHÀO MỪNG CÁC EM ĐẾN VỚI BÀI HỌC HÔM NAY!
KHỞI ĐỘNG
1.17. Câu nào sau đây không là mệnh đề?
- Tam giác đều là tam giác có 3 cạnh bằng nhau.
- 3 < 1
- 4 - 5 = 1
- Bạn học giỏi quá!
1.18. Cho định lí “Nếu hai tam giác bằng nhau thì diện tích của chúng bằng nhau”. Mệnh đề nào sau đây là đúng?
- Hai tam giác bằng nhau là điều kiện cần để diện tích của chúng bằng nhau.
- Hai tam giác bằng nhau là điều kiện cần và đủ để chúng có diện tích bằng nhau.
- Hai tam giác có diện tích bằng nhau là điều kiện đủ để chúng bằng nhau.
- Hai tam giác bằng nhau là điều kiện đủ để diện tích của chúng bằng nhau.
1.19. Mệnh đề nào sau đây là mệnh đề đúng?
- x , x2 > 1 x > - 1
- x , x2 > 1 x > 1
- x , x > - 1 x2 > 1
- x , x > 1 x2 > 1
1.20. Cho tập hợp A = {a, b, c}. Tập A có tất cả bao nhiêu tập con?
- 4
- 6
- 8
- 10
1.21. Cho các tập hợp A, B được minh họa bằng
biểu đồ Ven như hình bên. Phần tô màu xám trong
hình là biểu diễn của tập hợp nào sau đây?
- A B
- A B
- A \ B
- B \ A
BÀI TẬP CUỐI CHƯƠNG I (1 Tiết)
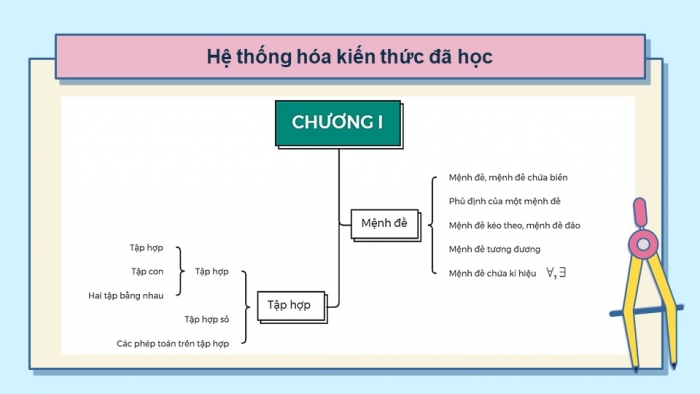
Hệ thống hóa kiến thức đã học
LUYỆN TẬP
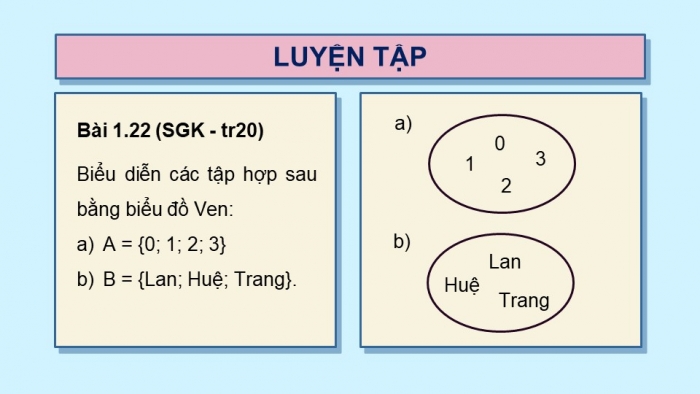
Bài 1.22 (SGK - tr20)
Biểu diễn các tập hợp sau bằng biểu đồ Ven:
- A = {0; 1; 2; 3}
- B = {Lan; Huệ; Trang}.
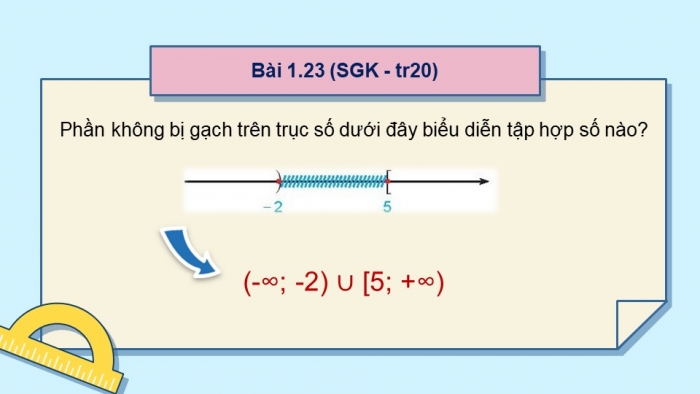
Bài 1.23 (SGK - tr20)
Phần không bị gạch trên trục số dưới đây biểu diễn tập hợp số nào?
Bài 1.24 (SGK - tr21)
Cho A = {x ∈ | x < 7}; B = {1; 2; 3; 6; 7; 8}. Xác định các tập hợp sau: A ∪ B; A ∩ B; A∖B
Giải
A ∪ B = {0; 1; 2; 3; 4; 5; 6; 7; 8}
A ∩ B = {1; 2; 3; 6}
A∖B = {0; 4; 5}.
Bài 1.25 (SGK - tr21)
Cho hai tập hợp A = [-2; 3] và B = (1; +∞). Xác định các tập hợp sau:
A ∩ B; B∖A;
A ∩ B = (1;3]
B∖A = (3; +∞)
= (-∞; 1].
Bài 1.26 (SGK - tr21)
Xác định các tập hợp sau và biểu diễn chúng trên trục số.
- a) (−∞; 1) ∩ (0; +∞)
- b) (4; 7] ∪ (−1; 5)
- c) (4; 7] \ (-3; 5]
Bài 1.27 (SGK - tr21)
Một cuộc khảo sát về khách du lịch thăm vịnh Hạ Long cho thấy trong 1410 khách du lịch được phỏng vấn có 789 khách du lịch đến thăm động Thiên Cung, 690 khách du lịch đến đảo Titop. Toàn bộ khách được phỏng vấn đã đến ít nhất một trong hai địa điểm trên. Hỏi có bao nhiêu khách du lịch vừa đến thăm động Thiên Cung vừa đến thăm đảo Titop ở vịnh Hạ Long?
Giải
Áp dụng công thức n(A ∪ B) = n(A) + n(B) - n(A ∩ B), với A là tập hợp khách du lịch thăm vịnh Hạ Long có đến thăm động Thiên Cung; B là tập hợp khách du lịch thăm vịnh Hạ Long có đến thăm đảo Titop.
Khi đó A ∩ B là tập hợp khách du lịch vừa đến thăm động Thiên Cung và vừa đến đảo Titop trong vịnh Hạ Long.
Ta có: 1410 = 789 + 690 - n(A ∩ B) nên n(A ∩ B) = 69.
Từ đó suy ra có 69 khách du lịch vừa đến thăm động Thiên Cung và vừa đến đảo Titop trong vịnh Hạ Long.
VẬN DỤNG
Câu 1: Tập A = {0; 2; 4; 6} có bao nhiêu tập hợp con có đúng hai phần tử?
- 4 B. 6 C. 7 D. 8
Câu 2: Cho A = {0; 1; 2; 3; 4}; B = {2; 3; 4; 5; 6 }. Tập hợp (A\ B) ∪ (B\ A) bằng:
- {0; 1; 5; 6 } B. {1; 2 } C. {2; 3; 4 } D. {5; 6 }
Câu 3
Cho hai tập hợp
A = {x ∈ , x + 3 < 4 + 2x} và B = {x ∈ , 5x - 3 < 4x - 1}. Tìm tất cả các số tự nhiên thuộc cả hai tập A và B.
- 0 và 1 1
- 0 D. Không có.
Câu 4
Cho số thực a < 0 và hai tập hợp A = (-∞;9 a), B = ( ; +∞). Tìm a để A ∩ B ≠ ∅.
- a = - - ≤ a < 0
- - < a <0 D. a < -
Câu 5: Lớp 10B1 có 7 học sinh giỏi Toán, 5 học sinh giỏi Lý, 6 học sinh giỏi Hóa, 3 học sinh giỏi cả Toán và Lý, 4 học sinh giỏi cả Toán và Hóa, 2 học sinh giỏi cả Lý và Hóa, 1 học sinh giỏi cả 3 môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một môn (Toán, Lý, Hóa) của lớp 10B1 là bao nhiêu?
Giải
Ta dùng biểu đồ Ven để giải:
Nhìn vào biểu đồ, số học sinh giỏi ít nhất 1 trong 3 môn là:
1 + 2 + 1 + 3 + 1 + 1 + 1 = 10.
Bài tập làm thêm
Câu 1: Có bao nhiêu giá trị nguyên dương của m để [m ; m + 1]\ (3; +∞) ≠ ∅?
Câu 2: Có bao nhiêu tập hợp X thỏa: {a; b} ⊂ X ⊂ {a; b; c; d; e}?
Câu 3: Tìm m để trong tập hợp A= m - 1; m ∩ (3; 5) có đúng một số tự nhiên?
Câu 4: Tập hợp A= {x = | x ∈ ; n ∈ } có bao nhiêu tập hợp con?
HƯỚNG DẪN VỀ NHÀ
Ôn tập kiến thức chương I
Hoàn thành bài tập về nhà và bài tập trong SBT
Chuẩn bị bài sau Bài 3: Bất phương trình bậc nhất hai ẩn
HẸN GẶP LẠI CẢ LỚP TRONG TIẾT HỌC SAU!
Giáo án điện tử toán 7 kết nối tri thức, giáo án powerpoint toán 7 KNTT bài: Bài tập cuối chương I (1 tiết), bài giảng điện tử toán 7 Kết nối
Nâng cấp lên tài khoản VIP để tải tài liệu và dùng thêm được nhiều tiện ích khác
Xem thêm giáo án khác
Bài tập 1.35 trang 25 toán 7 tập 1 KNTT
Hình 1.14 mô hỏng vị trí của 5 điểm A, B, C, D, E so với mực nước biển. Biết rằng độ cao ( đơn vị kilomet ) so với mực nước biển của mỗi điểm là một trong các số sau : $\frac{33}{12}$; $\frac{79}{30}$; $-\frac{25}{12}$; $-\frac{5}{6}$; 0 . Quan sát và cho biết độ cao của mỗi điểm.
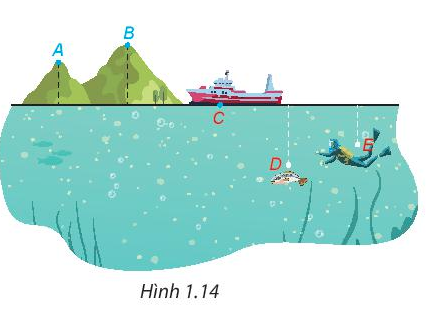
Hướng dẫn giải:
Độ cao của mỗi điểm sẽ là :
Điểm D: $-\frac{25}{12}$
Điểm E: $-\frac{5}{6}$
Điểm C: 0
Điểm A: $\frac{79}{30}$
Điểm B: $\frac{33}{12}$
Bài tập 1.36 trang 25 toán 7 tập 1 KNTT
Tính giá trị của các biểu thức sau :
a. $\frac{3^{12} + 3^{15}}{1+ 3^{3}}$
b. $ 2:\left ( \frac{1}{2} - \frac{2}{3}\right )^{2} + 0,125^{3}. 8^{3}- \left ( -12 \right )^{4}:6^{4}$
Hướng dẫn giải:
a. $\frac{3^{12} + 3^{15}}{1+ 3^{3}}$ = $\frac{3^{12} + 3^{3} .3^{12}}{1+ 3^{3}}$= $\frac{3^{12} (1 +3^{3} )}{1+ 3^{3}}$ = $3^{12}$
b. $ 2:\left ( \frac{1}{2} - \frac{2}{3}\right )^{2} + 0,125^{3}. 8^{3}- \left ( -12 \right )^{4}:6^{4}$= $ 2:\left ( \frac{3}{6} - \frac{4}{6}\right )^{2} + (0,125.8)^{3} - \left (12 \right )^{4}:6^{4}$ = 2:$(\frac{-1}{6})^{2}$ + 1 - $\left ( \frac{12}{6} \right )^{4}$ = 2: $\frac{1}{36}$ + 1 - $2^{4}$ = 72 + 1 -16 = 57
Bài tập 1.37 trang 25 toán 7 tập 1 KNTT
Chị Trang đang có 3 tháng thực tập tại Mỹ. Gần hết thời gian thực tập, chị Trang và bạn có kế hoạch tổ chức một bữa tiệc chia tay trước khi về nước. Chị ấy dự định mua 4 cái bánh Pizza. Mỗi cái giá 10,25 USD. Chị Trang có phiếu giảm giá 1,5 USD cho mỗi cái bánh Pizza. Hãy tính tổng tiền chị ấy dùng để mua bánh.
Hướng dẫn giải:
Số tiền chị ấy dùng để mua 1 cái bánh là : 10,25 - 1,5 = 8,75 USD
Vậy tổng tiền chị ấy dùng để mua bánh là : 8,75 x 4 = 35 USD
Bài tập 1.38 trang 25 toán 7 tập 1 KNTT
Bố của Hà chuẩn bị đi công tác bằng máy bay. Theo kế hoạch, máy bay sẽ cất cánh lúc 2 giờ 40 phút chiều. Bố của Hà cần phải có mặt ở sân bay trước ít nhất 2 giờ để làm thủ tục, biết rằng đi từ nhà Hà đến sân bay mất khoảng 45 phút. Hỏi bố của Hà phải đi từ nhà muộn nhất là lúc mấy giờ để đến sân bay cho kịp giờ bay?
Hướng dẫn giải:
2 giờ 40 phút chiều = 14 giờ 40 phút
Bố của Hà phải đi từ nhà để đến sân bay cho kịp giờ bay muộn nhất là lúc:
14 giờ 40 phút – 2 giờ - 45 phút = 11 giờ 55 phút
Vậy bố của Hà cần đi từ nhà muộn nhất là từ 11 giờ 55 phút.
