Soạn giáo án điện tử Toán 7 Kết nối bài 12: Tổng các góc trong một tam giác
Giáo án powerpoint toán 7 kết nối tri thức mới bài bài 12: Tổng các góc trong một tam giác. Giáo án soạn theo tiêu chí hiện đại, đẹp mắt với nhiều hình ảnh, nội dung, hoạt động phong phú, sáng tạo. Giáo án điện tử này dùng để giảng dạy online hoặc trình chiếu. Tin rằng, bộ bài giảng này sẽ hỗ trợ tốt việc giảng dạy và đem đến sự hài lòng với thầy cô.




Còn nữa....Giáo án khi tải về là bản đầy đủ. Có full siles bài giảng!
Nội dung giáo án
CHÀO MỪNG CÁC EM ĐẾN VỚI BÀI HỌC HÔM NAY!
KHỞI ĐỘNG
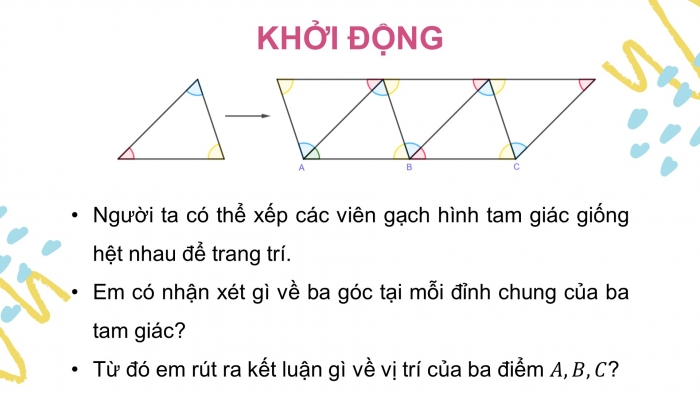
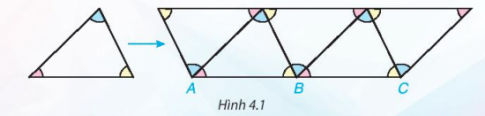
- Người ta có thể xếp các viên gạch hình tam giác giống hệt nhau để trang trí.
- Em có nhận xét gì về ba góc tại mỗi đỉnh chung của ba tam giác?
- Từ đó em rút ra kết luận gì về vị trí của ba điểm ?
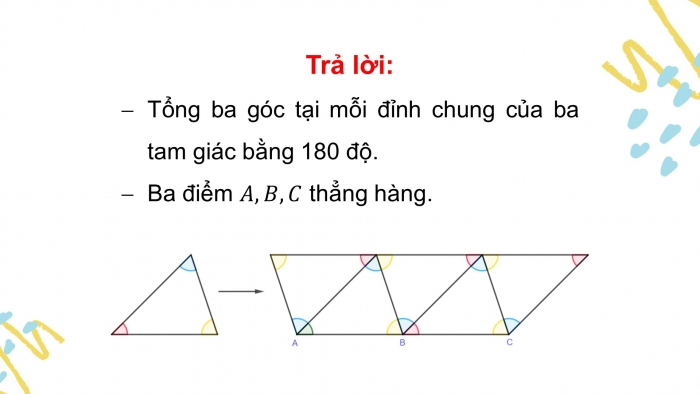
Trả lời:
- Tổng ba góc tại mỗi đỉnh chung của ba tam giác bằng 180 độ.
- Ba điểm thẳng hàng.
CHƯƠNG IV. TAM GIÁC BẰNG NHAU
BÀI 12: TỔNG CÁC GÓC TRONG MỘT TAM GIÁC
NỘI DUNG BÀI HỌC
Tổng các góc trong một tam giác.
Góc ngoài của tam giác.
- Tổng các góc trong một tam giác
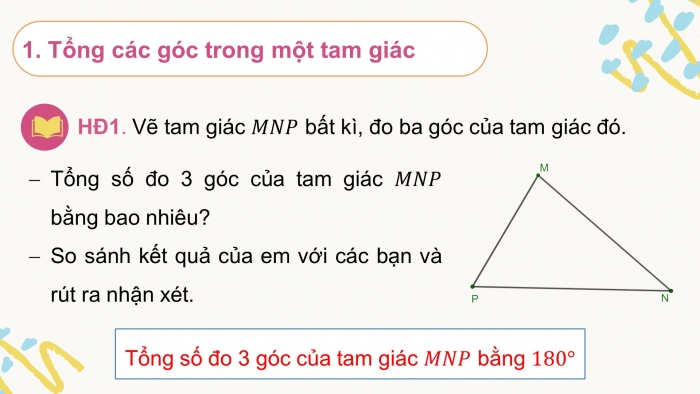
HĐ1. Vẽ tam giác bất kì, đo ba góc của tam giác đó.
- Tổng số đo 3 góc của tam giác bằng bao nhiêu?
- So sánh kết quả của em với các bạn và rút ra nhận xét.
- Tổng số đo 3 góc của tam giác bằng
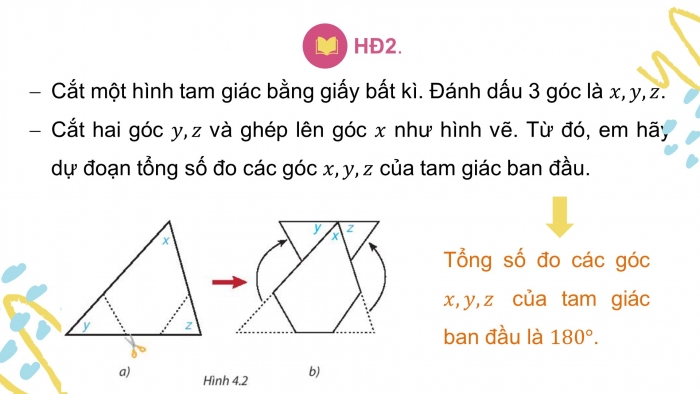
HĐ2.
- Cắt một hình tam giác bằng giấy bất kì. Đánh dấu 3 góc là .
- Cắt hai góc và ghép lên góc như hình vẽ. Từ đó, em hãy dự đoạn tổng số đo các góc của tam giác ban đầu.
- Tổng số đo các góc của tam giác ban đầu là .
Định lí: Tổng 3 góc trong một tam giác bằng .
Qua kẻ đường thẳng song song với .
(các cặp góc so le trong)
Do đó .
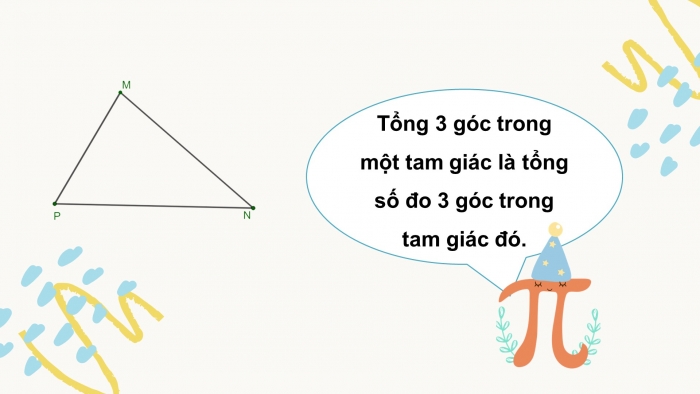
Tổng 3 góc trong một tam giác là tổng số đo 3 góc trong tam giác đó.
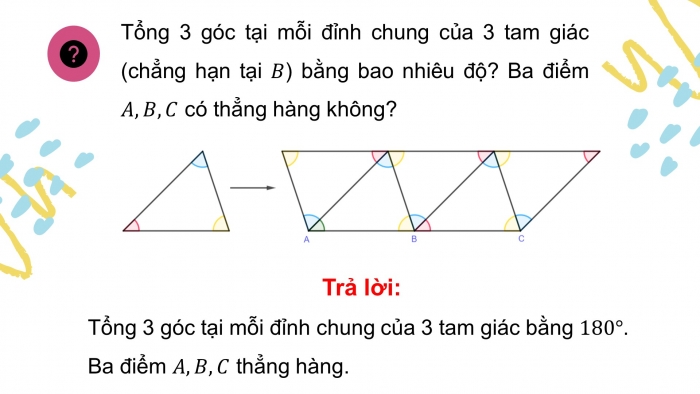
Tổng 3 góc tại mỗi đỉnh chung của 3 tam giác (chẳng hạn tại ) bằng bao nhiêu độ? Ba điểm có thẳng hàng không?
Trả lời:
Tổng 3 góc tại mỗi đỉnh chung của 3 tam giác bằng .
Ba điểm thẳng hàng.
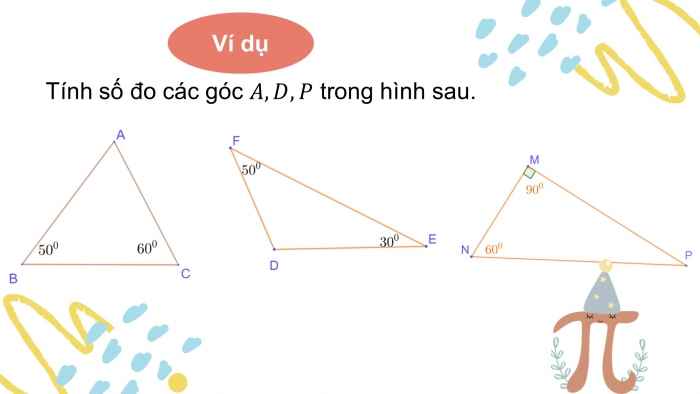
Ví dụ
Tính số đo các góc trong hình sau.
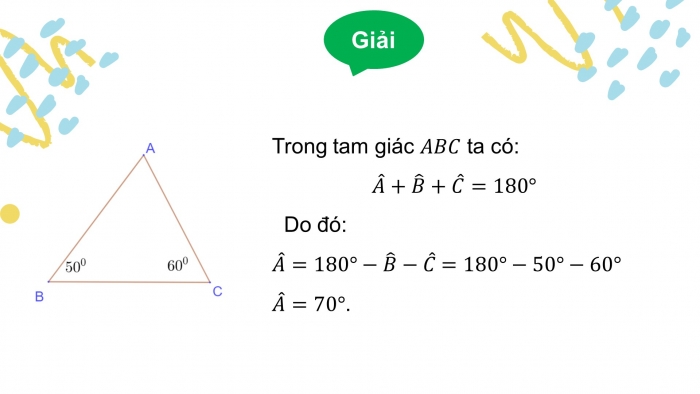
Giải
Trong tam giác ta có:
Do đó:
.
Trong tam giác ta có:
Do đó,
.
Trong tam giác ta có:
Do đó,
.
Chú ý:
- Tam giác có 3 góc đều nhọn là tam giác nhọn.
- Tam giác có 1 góc tù là tam giác tù.
- Tam giác có 1 góc vuông là tam giác vuông.
LUYỆN TẬP.
Cho tam giác vuông tại . Tính tổng hai góc và .
Giải
Xét tam giác ta có:
Giáo án điện tử toán 7 kết nối tri thức, giáo án powerpoint toán 7 KNTT bài 12: Tổng các góc trong một tam, bài giảng điện tử toán 7 Kết nối
Nâng cấp lên tài khoản VIP để tải tài liệu và dùng thêm được nhiều tiện ích khác
Xem thêm giáo án khác
TỔNG CÁC GÓC TRONG MỘT TAM GIÁC
Hoạt động 1: Vẽ tam giác MNP bất kì, đo ba góc của tam giác đó.
- Tổng số đo ba góc của tam giác MNP bằng bao nhiêu?
- So sánh kết quả của em với các bạn và rút ra nhận xét.

Hướng dẫn giải:
- Tổng số đo ba góc của tam giác MNP bằng 180 độ.
- So sánh kết quả với các bạn khác , rút ra nhận xét: Tổng ba góc của một tam giác bất kì bằng 180 độ.
Hoạt động 2: Cắt một hình tam giác bằng giấy bất kì (H.4.2a). Đánh dấu ba góc là x, y, z. Cắt hai góc y, z và ghép lên góc x như Hình 4.2b. Từ đó, em hãy dự đoán tổng số đo các góc x, y, z của tam giác ban đầu.

Hướng dẫn giải:
Tổng số đo các góc x,y,z của tam giác ban đầu ở hình a bằng số đo của góc bẹt ở hình b và bằng 180 độ.
Câu hỏi 1: Trở lại tình huống mở đầu, tổng ba góc tại mỗi đỉnh chung của ba tam giác (chẳng hạn tại B trong Hình 4.1) bằng bao nhiêu độ? Ba điểm A, B, C có thẳng hàng không?
Hướng dẫn giải:
- Tổng ba góc tại mỗi đỉnh chung của ba tam giác bằng 180 độ.
- Ba điểm A,B,C có thẳng hàng.
Luyện tập: Cho tam giác ABC vuông tại A. Tính tổng hai góc B và C.
Hướng dẫn giải:
Áp dụng định lí: Tổng ba góc của một tam giác bằng 180 độ.
=>$\widehat{B}$ +$\widehat{C}$ = $180^{\circ}$ - $\widehat{A}$ = $180^{\circ}$ - $90^{\circ}$ = $90^{\circ}$
Vận dụng: Cho tam giác ABC và Cx là tia đối của tia CB (H.4.5). Chứng minh rằng $\widehat{ACx}$ = $\widehat{BAC}$ + $\widehat{CBA}$

Hướng dẫn giải:
Vì Cx là tia đối của tia CB nên $\widehat{ACB}$ và $\widehat{ACx}$ là hai góc kề bù => $\widehat{ACB}$ + $\widehat{ACx}$ = $180^{\circ}$(1)
Mặt khác áp dụng định lí: Tổng ba góc của một tam giác bằng 180 độ. Ta suy ra :
$\widehat{BAC}$ + $\widehat{CBA}$ + $\widehat{ACB}$ =$180^{\circ}$ (2)
Từ (1) và (2) => $\widehat{ACx}$ = $\widehat{BAC}$ + $\widehat{CBA}$
