Soạn giáo án điện tử Toán 7 Kết nối bài: Luyện tập chung trang 74
Giáo án powerpoint toán 7 kết nối tri thức mới bài bài: Luyện tập chung trang 74. Giáo án soạn theo tiêu chí hiện đại, đẹp mắt với nhiều hình ảnh, nội dung, hoạt động phong phú, sáng tạo. Giáo án điện tử này dùng để giảng dạy online hoặc trình chiếu. Tin rằng, bộ bài giảng này sẽ hỗ trợ tốt việc giảng dạy và đem đến sự hài lòng với thầy cô.







Còn nữa....Giáo án khi tải về là bản đầy đủ. Có full siles bài giảng!
Nội dung giáo án
\
CHÀO MỪNG CÁC EM ĐẾN VỚI LỚP HỌC
KHỞI ĐỘNG
Em hãy nêu trường hợp bằng nhau thứ hai và thứ ba của hai tam giác?
Các em hãy trả lời nhanh các câu hỏi trắc nghiệm sau
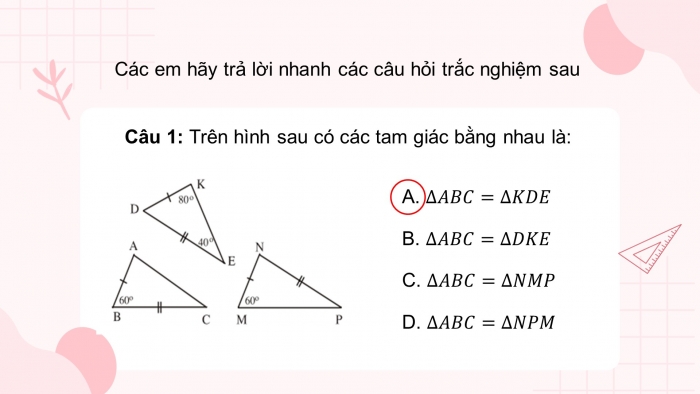
Câu 1: Trên hình sau có các tam giác bằng nhau là:
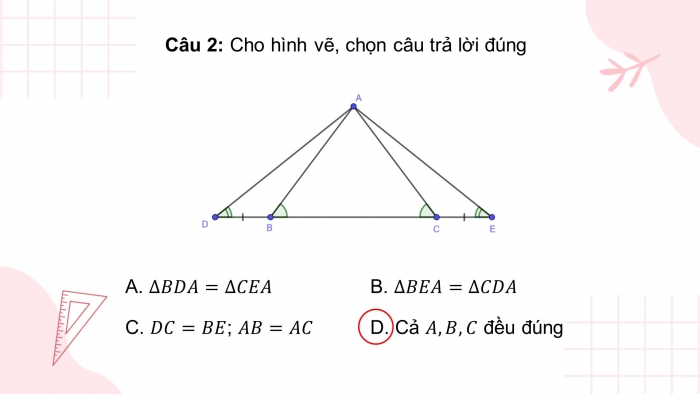
Câu 2: Cho hình vẽ, chọn câu trả lời đúng
- B.
- ; D. Cả đều đúng
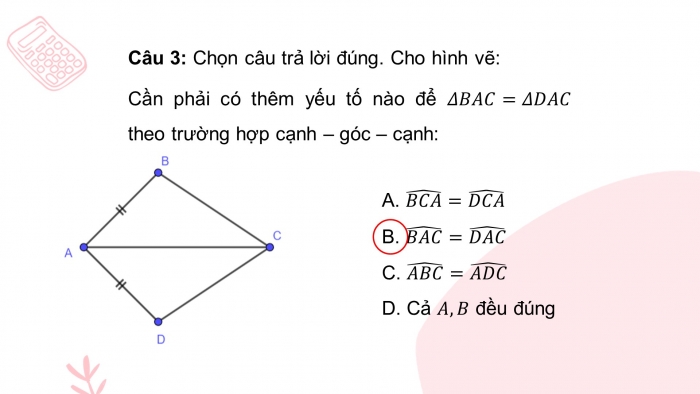
Câu 3: Chọn câu trả lời đúng. Cho hình vẽ:
Cần phải có thêm yếu tố nào để theo trường hợp cạnh – góc – cạnh:
- Cả đều đúng
Câu 4: Cho tam giác có . Tia phân giác của góc cắt tại . Ta có
- Cả đều đúng.
LUYỆN TẬP CHUNG
Ví dụ
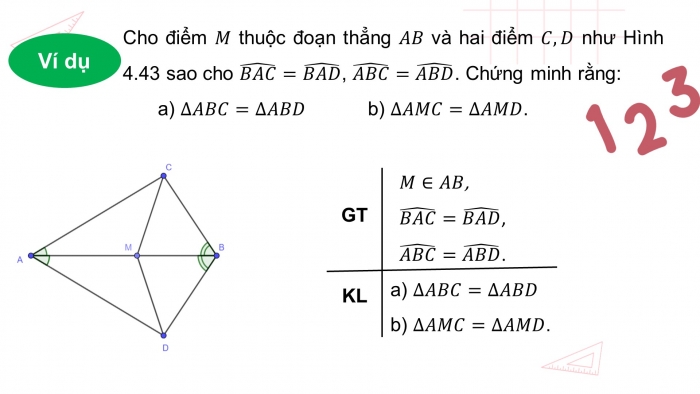
Cho điểm thuộc đoạn thẳng và hai điểm như Hình 4.43 sao cho , . Chứng minh rằng:
- a) b) .
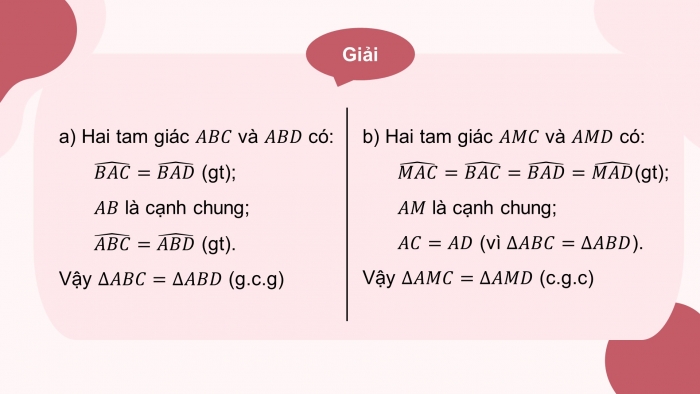
Giải
- a) Hai tam giác và có:
(gt);
là cạnh chung;
(gt).
Vậy (g.c.g)
- b) Hai tam giác và có:
(gt);
là cạnh chung;
(vì ).
Vậy (c.g.c)
LUYỆN TẬP
Bài 4.16 (SGK – tr.74) Cho hai tam giác và thoả mãn , , , , . Tính độ dài cạnh và số đo các góc , , .
Giải
Xét có:
Xét và có:
, , (gt)
Do đó (c.g.c)
suy ra
,
.
Bài 4.17 (SGK – tr.74) Cho hai tam giác và thoả mãn , , , . Tính độ dài cạnh .
Giải
Xét và có:
(gt),
Do đó (g.c.g)
suy ra .
Bài 4.18 (SGK – tr.74) Cho Hình 4.44, biết và . Chứng minh rằng
- a) b) .
Giải
- a) Xét và có:
;
;
là cạnh chung.
Do đó (c.g.c)
VẬN DỤNG
Bài 4.19 (SGK – tr.74) Cho tia là tia phân giác của góc . Lấy các điểm lần lượt thuộc các tia sao cho .
- a) Chứng minh rằng .
- b) Lấy điểm trên tia đối của tia . Chứng minh rằng .
Giáo án điện tử toán 7 kết nối tri thức, giáo án powerpoint toán 7 KNTT bài: Luyện tập chung trang 74, bài giảng điện tử toán 7 Kết nối
Nâng cấp lên tài khoản VIP để tải tài liệu và dùng thêm được nhiều tiện ích khác
Xem thêm giáo án khác
Bài tập 4.16 trang 74 toán 7 tập 1 KNTT
Cho tam giác ABC và DEF thỏa mãn AB= DE; AC=DF; $\widehat{BAC}$= $\widehat{DEF}$ = $60^{\circ}$ ; BC= 6cm, $\widehat{ABC}$ = $45^{\circ}$. Tính độ dài cạnh EF và số đo các góc ACB, DEF, EFD.
Hướng dẫn giải:
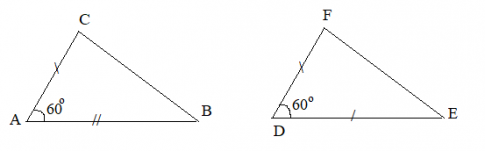
Xét hai tam giác ABC và DEF có:
- AB=DE
- AC=DF
- $\widehat{BAC}$= $\widehat{EDF}$ = $60^{\circ}$
=> $\Delta $BAC = $\Delta $EDF(c-g-c)
Từ đó ta suy ra:
- EF =BC= 6cm.
- $\widehat{ABC}$= $\widehat{DEF}$ = $45^{\circ}$
Áp dụng định lý tổng ba góc trong một tam giác bằng $180^{\circ}$ . Vậy ttrong tam giác ABC sẽ có :
$\widehat{A}$ + $\widehat{B}$ + $\widehat{C}$= $180^{\circ}$ => $\widehat{C}$ = $180^{\circ}$- ($\widehat{A}$ + $\widehat{B}$) = $180^{\circ}$-( $60^{\circ}$+ $45^{\circ}$) = $75^{\circ}$
Vì $\Delta $BAC = $\Delta $EDF(c-g-c) => $\widehat{F}$ = $\widehat{C}$ = $75^{\circ}$
Bài tập 4.17 trang 74 toán 7 tập 1 KNTT
Cho hai tam giác ABC và DEF thoả mãn AB=DE; AB=DE, $\widehat{ABC} = \widehat{DEF} = 70^{\circ}$ ; $\widehat{BAC} = \widehat{EDF} = 60^{\circ}$ ,AC=6cm. Tính độ dài cạnh DF.
Hướng dẫn giải:
Xét hai tam giác ABC và DEF ta có :
- $\widehat{A} = \widehat{D} = 60^{\circ}$
- AB= DE
- $\widehat{B} = \widehat{E} = 70^{\circ}$
=> $\Delta$ABC = $\Delta$DEF (g-c-g)
=> DF= AC = 6cm
Bài tập 4.18 trang 74 toán 7 tập 1 KNTT
Cho Hình 4.44, biết EC=ED; và $\widehat{AEC}$ = $\widehat{AED}$. Chứng minh rằng:
a. ΔAEC=ΔAED
b. ΔABC=ΔABD

Hướng dẫn giải:
a. Xét ΔAEC và ΔAED, ta có :
- EC= ED
- $\widehat{AEC}$ = $\widehat{AED}$
- Cạnh AE chung
=> ΔAEC = ΔAED (c-g-c)
=> AC = AD (*)
b. Ta có :
$\widehat{AEC}$ và $\widehat{CEB}$ là 2 góc kề bù => $\widehat{AEC}$ + $\widehat{CEB}$ = $180^{\circ}$ => $\widehat{CEB}$ = $180^{\circ}$- $\widehat{AEC}$ (1)
$\widehat{AED}$ và $\widehat{DEB}$ là 2 góc kề bù => $\widehat{AED}$ + $\widehat{DEB}$ = $180^{\circ}$ => $\widehat{DEB}$ = $180^{\circ}$- $\widehat{AED}$ (2)
Mà $\widehat{AEC}$ = $\widehat{AED}$ kết hợp với (1) và (2)=> $180^{\circ}$- $\widehat{AEC}$ = $180^{\circ}$- $\widehat{AED}$=> $\widehat{AEC}$ = $\widehat{AED}$
Xét ΔCEB và ΔDEB, ta có :
- CE= DE
- $\widehat{AEC}$ = $\widehat{AED}$
- EB chung
=> ΔCEB = ΔDEB
=> CB= DB (3)
Kết hợp với (*), xét ΔABC và ΔABD :
- CB= DB (3)
- AC = AD (*)
- AB chung
=> ΔABC = ΔABD
Bài tập 4.19 trang 74 toán 7 tập 1 KNTT
Cho tia Oz là tia phân giác của góc xOy. Lấy các điểm A,B,C lần lượt thuộc các tia Ox, Oy, Oz sao cho $\widehat{CAO}$= $\widehat{CBO}$
a. Chứng minh rằng ΔOAC=ΔOBC
b. Lấy điểm M trên tia đối của tia CO. Chứng minh rằng ΔMAC=ΔMBC
Hướng dẫn giải:
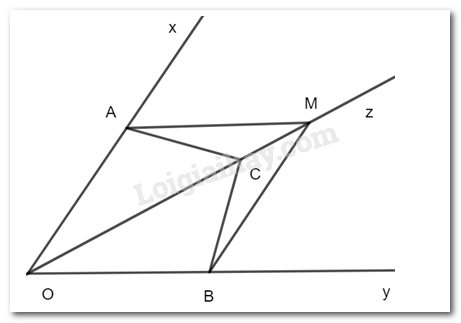
a.
Xét hai tam giác OAC và OBC có
- $\widehat{AOC}$= $\widehat{AOB}$
- OC chung
- $\widehat{ACO}$= $\widehat{ABO}$ (Áp dụng định lý tổng 3 góc trong một tam giác bằng $180^{\circ}$)
=> $\Delta $OAC và $\Delta $OBC (g-c-g)
b. Từ câu a ta suy ra :
- AO= BO
- AC= BC
Xét 2 tam giác AOM và BOM, ta có :
- AO= BO
- $\widehat{AOM}$= $\widehat{BOM}$
- OM chung
=> $\Delta $AOM và $\Delta $BOM (g-c-g)
=> AM= BM
Xét ΔMAC và ΔMBC , ta có :
- AM= BM
- AC= BC
- MC chung
=> ΔMAC = ΔMBC (c-c-c)
