Giáo án điện tử toán 7 kết nối tri thức

Soạn giáo án điện tử Toán 7 Kết nối bài 3: Lũy thừa với số mũ tự nhiên của một số hữu tỉ (3 tiết)

Giáo án powerpoint toán 7 kết nối tri thức mới bài bài 3: Lũy thừa với số mũ tự nhiên của một số hữu tỉ (3 tiết). Giáo án soạn theo tiêu chí hiện đại, đẹp mắt với nhiều hình ảnh, nội dung, hoạt động phong phú, sáng tạo. Giáo án điện tử này dùng để giảng dạy online hoặc trình chiếu. Tin rằng, bộ bài giảng này sẽ hỗ trợ tốt việc giảng dạy và đem đến sự hài lòng với thầy cô.

Cùng hệ thống với: Kenhgiaovien.com - Zalo hỗ trợ: Fidutech - nhấn vào đây

Còn nữa....Giáo án khi tải về là bản đầy đủ. Có full siles bài giảng!


Tải về

Nội dung giáo án

CHÀO MỪNG CÁC EM THAM DỰ BUỔI HỌC HÔM NAY!

Trái Đất, ngôi nhà chung của chúng ta có khoảng 71% diện tích bề mặt được bao phủ bởi nước. Nếu gom hết toàn bộ lượng nước trên Trái Đất để đổ đầy vào một bể chứa hình lập phương thì kích thước cạnh của bể phải lên tới 1111,34 km.

  • Muốn biết lượng nước trên Trái đất là khoảng bao nhiêu ta phải tính thế nào?
  • Biểu thức 1111,34 x 1111,34 x 1111,34 có thể viết gọn hơn dưới dạng lũy thừa giống như lũy thừa của một số tự nhiên mà em được học ở lớp 6 không?

BÀI 3: LŨY THỪA VỚI SỐ MŨ TỰ NHIÊN CỦA MỘT SỐ HỮU TỈ (3 Tiết)

NỘI DUNG BÀI HỌC

Lũy thừa với số mũ tự nhiên

Nhân và chia hai lũy thừa cùng cơ số

Lũy thừa của lũy thừa

Lũy thừa với số mũ tự nhiên

Thảo luận nhóm đôi, hoàn thành HĐ1, HĐ2, HĐ3.

Viết các tích sau dưới dạng lũy thừa rồi chỉ ra cơ số và số mũ của lũy thừa đó.

HĐ2:

Thực hiện phép tính:

  1. a) (-2). (-2). (-2) c) . . . =

= -8

  1. b) (-0,5). (-0,5) = 0,25

HĐ3:

Hãy viết các biểu thức trong HĐ2 dưới dạng lũy thừa tương tự như lũy thừa của số tự nhiên.

Giải

  1. a) (-2).(-2).(-2) = (-2)3 b) (-0,5).(-0,5) = (-0,5)2

Định nghĩa

Lũy thừa bậc n của một số hữu tỉ x, kí hiệu xn, là tích của n thừa số x (n là số tự nhiên lớn hơn 1):

 = x. x. x.... . x (x   , n , n > 1)

n thừa số x

Cách gọi:   x: cơ số;       n: Số mũ   

Quy ước:   x1 = x;           x0 = 1 (x 0)

Ví dụ 1: Tính

  1. a) (-3)3 b)

Giải

  1. (-3)3 = (-3). (-3). (-3) = -27
  2. b) = . . . = =

Luyện tập 1: Tính

  1. a) b) (0,7)3

Giải

  1. b) (0,7)3 = (0,7).(0,7).(0,7) = 0,343

Đọc Ví dụ 2 và nêu cách so sánh

Ví dụ 2:

Tính và so sánh:

  1. 22. 32 và (2. 3)2 b)  và

Giải:

  1. 22. 32 = 4. 9 = 36 và (2. 3)2 = 62 = 36 nên 22. 32 = (2. 3)2

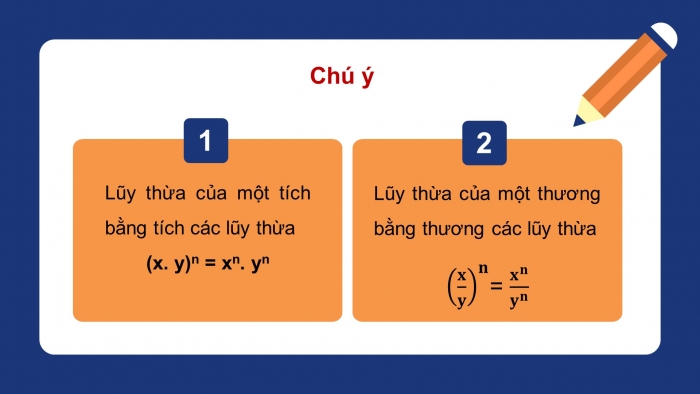
Chú ý:

Lũy thừa của một tích bằng tích các lũy thừa

(x. y)n = xn. yn

Lũy thừa của một thương bằng thương các lũy thừa

=

Luyện tập 2: Tính

  1. a) . 310

=  . 310

= 210

(-125)3 : 253

= (-125 : 25)3

= (-5)3 = -125

  1. c) (0,08)3 . 103

Vận dụng

Viết công thức tính thể tích hình lập phương cạnh a dưới dạng lũy thừa. Từ đó viết biểu thức lũy thừa để tính toàn bộ lượng nước trên Trái Đất trong bài toán mở đầu (đơn vị kilômét khối).

Giải

Lượng nước trên Trái Đất là:

1111,343 ≈ 1 372 590 024 (km3).

Chú ý

Lũy thừa của một tích bằng tích các lũy thừa

(x. y)n = xn. yn

Lũy thừa của một thương bằng thương các lũy thừa

=

Luyện tập 2: Tính

  1. a) . 310 b) (-125)3 : 253 c) (0,08)3 . 103     

=  . 310

= 210

Vận dụng

Viết công thức tính thể tích hình lập phương cạnh a dưới dạng lũy thừa. Từ đó viết biểu thức lũy thừa để tính toàn bộ lượng nước trên Trái Đất trong bài toán mở đầu (đơn vị kilômét khối).

Giải

Lượng nước trên Trái Đất là:

1111,343 ≈ 1 372 590 024 (km3).

Nhân và chia hai lũy thừa cùng cơ số

Thảo luận nhóm đôi, hoàn thành HĐ4.

HĐ4

Tính và so sánh:

  1. a) (-3)2. (-3)4 và (-3)6 b) 0,63 : 0,62 và 0,6.
  2. a) (-3)2.(-3)4 = 9. 81 = 729; (-3)6 = 729

Vậy (-3)2.(-3)4 = (-3)6

  1. b) (0,6)3: 0,62 = 0,216: 0,36 = 0,6

Vậy (0,6)3: 0,62 = 0,6.

Tính chất

  • Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng hai số mũ.

xm . xn = xm + n 

  • Khi chia hai lũy thừa cùng cơ số khác 0, ta giữ nguyên cơ số và lấy số mũ của lũy thừa bị chia trừ số mũ của lũy thừa số chia.

xm : xn = xm - n (x  0; m ≥ 0)

Ví dụ 3

Tính: a) . ;                 b) (-5)5 : (-5)5

Giải:

  1. b) (-5)5 : (-5)5 = (-5)5-5

    = (-5)0 = 1.

Luyện tập 3

Viết kết quả của các phép tính sau dưới dạng lũy thừa:

  1. a) (-2)3. (-2)4; = (-2)3+4 = (-2)7
  2. b) (0,25)7 : (0,25)3= (0,25)7-3 = (0,25)4

Lũy thừa của lũy thừa

Thảo luận nhóm đôi, hoàn thành HĐ5.

HĐ5

Viết số (22)3 dưới dạng lũy thừa cơ số 2 và số [(-3)2]2 dưới dạng lũy thừa cơ số -3.

Giải

  • (22)3 = 22. 22. 22 = 22+2+2 = 26
  • [(-3)2]2 = (-3)2. (-3)2 = (-3)2+2 = (-3)4

KẾT LUẬN

Khi tính lũy thừa của một lũy thừa, ta giữ nguyên cơ số và nhân hai số mũ.

(xm)n = xm. xn

Ví dụ 4: Tính [(-5)3]7

Giải:

[(-5)3]7 = (-5)3.7 = (-5)21.

Luyện tập 4: Viết các số  và  dưới dạng lũy thừa cơ số .

Giải:

Thử thách nhỏ

Cho hình vuông như Hình 1.12. Em hãy thay dấu “?” bằng một lũy thừa của 2, biết tích các lũy thừa trên mỗi hàng, mỗi cột và mỗi đường chéo đều bằng nhau.

LUYỆN TẬP

Bài 1.19 (SGK - tr18)

Viết các số ;  dưới dạng lũy thừa cơ số .

Giải

Bài 1.21 (SGK - tr19)

Không sử dụng máy tính, hãy tính:

  1. a) (-3)8, biết (-3)7 = -2 187; b) , biết =  

Giải

  1. a) (-3)8 = (-3)7. (-3) = -2 187. (-3) = 6 561

Bài 1.22 (SGK - tr19

Viết các biểu thức sau dưới dạng lũy thừa của một số hữu tỉ.

  1. a) 158. 24 b) 275 : 323

Giải

  1. 158. 24 = (152)4. 24 = (152. 2)4 = 4504
  2. 275 : 323 = (33)5 : (25)3 = 315 : 215 =

VẬN DỤNG

Bài 1.24 (SGK - tr19)

Khoảng cách từ Trái Đất đến Mặt Trời bằng khoảng 1,5. 108 km. Khoảng cách từ Mộc tinh đến Mặt Trời khoảng 7,78. 108 km. Hỏi khoảng cách từ Mộc tinh đến Mặt Trời gấp khoảng bao nhiêu lần khoảng cách từ Trái Đất đến Mặt Trời?

Giải

Ta có: 7,78. 108 : (1,5 . 108) =

Vậy khoảng cách từ Mộc tinh đến Mặt Trời gấp khoảng  lần khoảng cách từ Trái Đất đến Mặt Trời.

Bài 1. 25 (SGK - tr19)

Bảng thống kê bên cho biết số lượt khách quốc tế đến thăm Việt Nam trong năm 2019.

Em hãy sắp xếp tên các quốc gia theo thứ tự số lượng khách đến thăm Việt Nam từ nhỏ đến lớn.

HƯỚNG DẪN VỀ NHÀ

Ghi nhớ kiến thức đã học

Hoàn thành bài tập SGK và làm bài tập trong SBT

Chuẩn bị bài sau - Bài 4

CẢM ƠN SỰ QUAN TÂM VÀ THEO DÕI CỦA CÁC EM!


=> Xem toàn bộ Giáo án điện tử toán 7 kết nối tri thức

Từ khóa tìm kiếm:

Giáo án điện tử toán 7 kết nối tri thức, giáo án powerpoint toán 7 KNTT bài 3: Lũy thừa với số mũ tự, bài giảng điện tử toán 7 Kết nối

Nâng cấp lên tài khoản VIP để tải tài liệu và dùng thêm được nhiều tiện ích khác

Chat hỗ trợ - 0386 168 725

Xem thêm giáo án khác

1. LŨY THỪA VỚI SỐ MŨ TỰ NHIÊN

Thực hành 1: Tính

$\left ( \frac{-2}{3} \right )^{3}$ ; $\left ( \frac{-3}{5} \right )^{2}$; (-0,5)3;  (-0,5)2; (37,57)0; (3,57)1

Hướng dẫn giải:

$\left ( \frac{-2}{3} \right )^{3}$ = $\frac{-8}{27}$  ;  $\left ( \frac{-3}{5} \right )^{2}$ = $\frac{9}{25}$ ;

(-0,5)3 =$\left ( \frac{-1}{2} \right )^{3}$ = $\frac{-1}{8}$ ; (-0,5)2 = =$\left ( \frac{-1}{2} \right )^{2}$ = $\frac{1}{4}$ 

(37,57)0 = 1 ; (3,57)1 = 3,57

2. TÍCH VÀ THƯƠNG CỦA HAI LŨY THỪA CÙNG CƠ SỐ

Hoạt động khám phá 1: Tìm số thích hợp thay vào dấu "?" trong các câu dưới đây:

a) $\left ( \frac{1}{3} \right )^{2}$ . $\left ( \frac{1}{3} \right )^{2}$ = $\left ( \frac{1}{3} \right )^{?}$;

b) (0,2)2 . (0,2)3 = (0,2)? 

Hướng dẫn giải: 

a) $\left ( \frac{1}{3} \right )^{2}$ . $\left ( \frac{1}{3} \right )^{2}$ = $\left ( \frac{1}{3} \right )^{4}$;

b) (0,2)2 . (0,2)3 = (0,2)5

Thực hành 2:  Tính:

a)  ${{(-2)}^{2}}.{{(-2)}^{3}}$

b) ${{\text{(-0,25)}}^{\text{7}}}\text{:(-0,25}{{\text{)}}^{\text{5}}}$

c) ${{\left( \frac{3}{4} \right)}^{4}}.{{\left( \frac{3}{4} \right)}^{3}}$

Hướng dẫn giải: 

a)  ${{(-2)}^{2}}.{{(-2)}^{3}}={{(-2)}^{5}}$

b) ${{\text{(-0,25)}}^{\text{7}}}\text{:(-0,25}{{\text{)}}^{\text{5}}}={{\text{(-0,25)}}^{2}}$$={{\left( \frac{1}{4} \right)}^{2}}=\frac{1}{16}$

c) ${{\left( \frac{3}{4} \right)}^{4}}.{{\left( \frac{3}{4} \right)}^{3}}=\frac{3}{4}$

3. LŨY THỪA CỦA LŨY THỪA

Hoạt động khám phá 2: Tính và so sánh

 a)  [(-2)2 ]3 và (-2)6

b) $\left [ \left ( \frac{1}{2} \right )^{2} \right ]^{2}$ và $\left ( \frac{1}{2} \right )^{4}$

Hướng dẫn giải:

a)  [(-2)2 ]3 = (-2)6 

b) $\left [ \left ( \frac{1}{2} \right )^{2} \right ]^{2}$ = $\left ( \frac{1}{2} \right )^{4}$ 

Thực hành 3: Thay số thích hợp vào dấu "?" trong các câu sau:

a) $\left [ \left ( \frac{-2}{3} \right )^{2} \right ]^{5}$ = $\left ( \frac{2}{3} \right )^{?}$ 

b)  [(0,4)3 ]3 = (0,4)?

c)  [(7,31)3 ]0 = ?

Hướng dẫn giải:

a) $\left [ \left ( \frac{-2}{3} \right )^{2} \right ]^{5}$ = $\left ( \frac{2}{3} \right )^{10}$ 

b)  [(0,4)3 ]3 = (0,4)9

c)  [(7,31)3 ]0 = 1

Vận dụng: Để viết những số có giá trị lớn, người ta thường viết các số ấy dưới dạng tích của lũy thừa cơ số 10 với một số lớn hơn hoặc bằng 1 nhưng nhỏ hơn 10. Chẳng hạn khoảng cách trung bình giữa Mặt Trời và Trái Đất là 149 600 000 km được viết là 1,496 . 108 km.

Hãy dùng cách viết trên để viết các đại lượng sau:

a) Khoảng cách từ Mặt Trời đến Sao Thủy dài khoảng 58 000 000 km.

b) Một năm ánh sáng có độ dài khoảng 9 460 000 000 km.

Hướng dẫn giải:

a) Khoảng cách từ Mặt Trời đến Sao Thủy dài khoảng 58 000 000 km  được viết là: 5,8 . 107 km.

b) Một năm ánh sáng có độ dài khoảng 9 460 000 000 km được viết là: 9,46 . 109 km.