Soạn giáo án điện tử Toán 7 Kết nối bài 1: Tập hợp các số hữu tỉ
Giáo án powerpoint toán 7 kết nối tri thức mới bài bài 1: Tập hợp các số hữu tỉ. Giáo án soạn theo tiêu chí hiện đại, đẹp mắt với nhiều hình ảnh, nội dung, hoạt động phong phú, sáng tạo. Giáo án điện tử này dùng để giảng dạy online hoặc trình chiếu. Tin rằng, bộ bài giảng này sẽ hỗ trợ tốt việc giảng dạy và đem đến sự hài lòng với thầy cô.










Còn nữa....Giáo án khi tải về là bản đầy đủ. Có full siles bài giảng!
Nội dung giáo án
CHÀO MỪNG CÁC EM ĐẾN VỚI BUỔI HỌC HÔM NAY!
KHỞI ĐỘNG
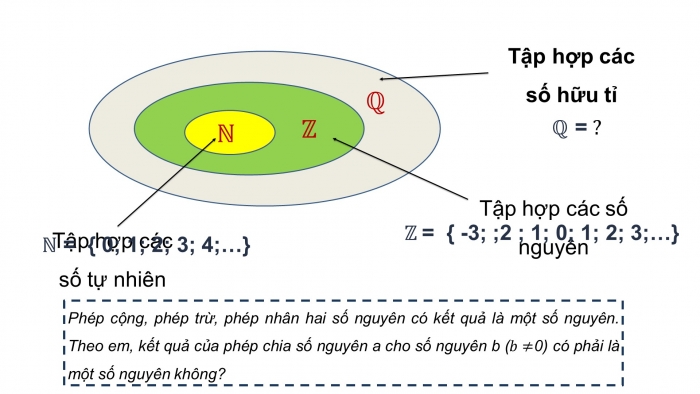
Phép cộng, phép trừ, phép nhân hai số nguyên có kết quả là một số nguyên. Theo em, kết quả của phép chia số nguyên a cho số nguyên b ( 0) có phải là một số nguyên không?
BÀI 1:
TẬP HỢP CÁC SỐ HỮU TỈ
NỘI DUNG
- Số hữu tỉ
- Thứ tự trong tập hợp số hữu tỉ
- Biểu diễn số hữu tỉ trên trục số
- Số đối của một số hữu tỉ
- Số hữu tỉ
HOẠT ĐỘNG NHÓM 4
HĐKP1
Cho các số -7; 0,5; 0; .
Với mỗi số, hãy viết một phân số bằng số đã cho.
Trả lời:
Các số -7; 0,5; 0; đều có thể viết dưới dạng phân số, người ta gọi đó là số hữu tỉ.
Vậy số hữu tỉ là gì?
Số hữu tỉ là số viết được dưới dạng phân số với a, b , b 0
Các phân số bằng nhau biểu diễn cùng một số hữu tỉ.
Tập hợp các số hữu tỉ được kí hiệu là .
HOẠT ĐỘNG CẶP ĐÔI
Ví dụ 1:
- Các số có là các số hữu tỉ không? Vì sao?
- Các số 3; -1,4; có là các số hữu tỉ không? Vì sao?
Giải:
Ví dụ 1:
- Các số là các số hữu tỉ . Vì các số là các phân số thỏa mãn điều kiện a, b , b
- Các số 3; -1,4; là các số hữu tỉ. Vì:
;
Nhận xét:
- Có vô số phân số bằng các phân số đã cho.
- Các phân số bằng nhau là các cách viết khác nhau của cùng một số hữu tỉ.
- Mỗi số nguyên là một số hữu tỉ.
Thực hành 1
Vì sao các số -0,33; 0; ; 0,25 là các số hữu tỉ?
Vì các số đó đều biểu diễn được dưới dạng phân số:
Vận dụng 1
Viết số đo các đại lượng sau dưới dạng ; với a, b , b
- 2,5 kg đường.
- 3,8 m dưới mực nước biển.
Giải:
- a) 2,5kg đường = kg đường.
- b) 3,8m = m
- THỨ TỰ TRONG TẬP HỢP SỐ HỮU TỈ
HĐKP2
- So sánh hai phân số và
- Trong mỗi trường hợp sau, nhiệt độ nào cao hơn?
- 0oC và -0,5oC; ii. -12oC và -7oC
Trả lời:
- a) Có 2 > -5 >
- b)
- Có 0oC > -0,5oC
- 12oC > -7oC
- Với hai số hữu tỉ bất kì x, y ta luôn có: hoặc x = y hoặc x < y hoặc x > y.
- Số hữu tỉ lớn hơn 0 gọi là số hữu tỉ dương.
- Số hữu tỉ nhỏ hơn 0 gọi là số hữu tỉ âm.
- Số hữu tỉ 0 không là số hữu tỉ dương cũng không là số hữu tỉ âm.
Ví dụ 2. So sánh các cặp số hữu tỉ sau:
- a) -0,5 và ; b) -1 và 0
- Giải:
Ta có: -0,5 = ; = . Vì -5 < -2 và 10 > 0, nên < .
Vậy -0,5 <
- b) Ta có: -1 = ; = . Vì -5 < 0 và 3 > 0, nên < .
Vậy -1 < 0
Thực hành 2: Cho các số hữu tỉ: ; ; 5,12; -3; ; -3,75
- So sánh với -3,75; với .
- Trong các số hữu tỉ đã cho, số nào là số hữu tỉ dương, số nào là số hữu tỉ âm, số nào không là số hữu tỉ dương cũng không là số hữu tỉ âm.
Giải:
- b) + Số hữu tỉ dương: ; 5,12 ; số hữu tỉ âm: ; -3; -3,75.
+ Số không là số hữu tỉ dương cũng không là số hữu tỉ âm.
3.BIỂU DIỄN SỐ HỮU TỈ TRÊN TRỤC SỐ
HĐKP3
- Biểu diễn các số nguyên -1; 1; -2 trên trục số.
- Quan sát hình 2. Hãy dự doán điểm A biểu diễn số hữu tỉ nào?
Giải:
- b) Điểm A biểu diễn số hữu tỉ:
Kết luận
- Trên trục số, mỗi số hữu tỉ được biểu diễn bởi một điểm. Điểm biểu diễn số hữu tỉ x được gọi là điểm x.
- Với hai số hữu tỉ bất kì x, y nếu x < y thì trên trục số nằm ngang, điểm x ở bên trái điểm y.
Ví dụ 3: Để biểu diễn số hữu tỉ ta làm như sau:
- Chia đoạn thẳng đơn vị thành bốn phần bằng nhau, ta được đoạn đơn vị mới bằng đơn vị cũ.
- Số hữu tỉ được biểu diễn bởi điểm A nằm bên phải điểm 0 và cách điểm 0 một đoạn bằng 3 đơn vị mới ( Hình 3).
Ví dụ 4: Để biểu diễn số hữu tỉ ta làm như thế nào?
HOẠT ĐỘNG NHÓM BA
- Chia đoạn thẳng đơn vị thành hai phần bằng nhau, ta được đoạn đơn vị mới bằng đơn vị cũ.
- Số hữu tỉ được biểu diễn bởi điểm B nằm bên trái điểm 0 và cách điểm 0 một đoạn bằng 3 đơn vị mới ( Hình 3).
Thực hành 3
- a) Các điểm M, N, P trong Hình 6 biểu diễn các số hữu tỉ nào?
- b) Biểu diễn các số hữu tỉ trên trục số: -0,75; ;
- Số đối của số hữu tỉ
HĐKP4
Em có nhận xét gì về vị trí điểm và ?
Trả lời:
Điểm và trên trục số cách đều và nằm về hai phía điểm gốc O.
- Hai số hữu tỉ có điểm biểu diễn trên trục số cách đều và nằm về hai phía điểm gốc O là hai số đối nhau, số này gọi là số đối của số kia.
- Số đối của số hữu tỉ x kí hiệu là –x.
Nhận xét
- a) Mọi số hữu tỉ đều có một số đối.
- b) Số đối của số 0 là số 0.
- c) Với hai số hữu tỉ âm, số nào có số đối lớn thì số đó nhỏ hơn.
- Số đối của là và ta viết là
Thực hành 4
Tìm số đối của mỗi số sau: 7; ; -0,75; 0;
Trả lời:
Số đối của các số : 7; ; -0,75; 0; lần lượt là:
-7; ; 0,75; 0; -
LUYỆN TẬP
- Thay ? bằng kí hiệu , thích hợp:
- Trong các phân số sau , những phân số nào biểu diễn số hữu tỉ ; ; ; - ; .
- b) Tìm số đối của mỗi số sau: 12; ; -0,375; ;
Giải:
- a) Những phân số biểu diễn số hữu tỉ là: ;
- b) Số đối của các số: 12; ; -0,375; ; lần lượt là:
-12; ; 0,375; ;
- a) Các điểm A, B, C trong Hình 8 biểu diễn số hữu tỉ nào?
- b) Biểu diễn các số hữu tỉ ; ; ; -0,8 trên trục số
Trả lời
- a) Các điểm A, B, C trong hình 8 biểu diễn các số hữu tỉ:
- b) Biểu diễn các số hữu tỉ ; ; ; -0,8 trên trục số
Vận dụng
Vận dụng 2. Bạn Hồng đã phát biểu: “4,1 lớn hơn 3,5. Vì thế -4,1 cũng lớn hơn -3,5”. Theo em, phát biểu của bạn Hồng có đúng không? Tại sao?
Trả lời:
Phát biểu của bạn Hồng sai. Vì -4,1 < -3,5.
- Bảng dưới đây cho biết độ cao của bốn rãnh đại dương so với mực nước biển.
- Những rảnh đại dương nào có độ cao hơn rãnh Puerto Rico? Giải thích.
- Rãnh đại dương nào có độ cao thấp nhất trong bốn rảnh trên? Giải thích.
- a) Có : -10,5 < -8,6 < -8,0 < -7,7
Vậy rãnh Philippine có độ cao cao hơn rãnh Peurto Rico.
- b) Có : -7,7 > -8,0 > -8,6 > -10,5
Vậy rãnh Romanche có độ cao thấp nhất trong bốn rãnh trên.
Câu hỏi 1:Tập hợp các số hữu tỉ kí hiệu là
- Q
- N
- *
- R
Câu hỏi 2: Chọn câu đúng
- -9
- 1,2
Câu hỏi 4: Với điều kiện nào của b thì phân số , là số hữu tỉ.
B # 0
HƯỚNG DẪN VỀ NHÀ
- Ghi nhớ các nội dung kiến thức đã học
- Hoàn thành nốt các bài tập 5, 6 ( SGK – tr10)+ bài tập SBT.
- Chuẩn bị bài mới “Các phép tính với số hữu tỉ”
CẢM ƠN CÁC BẠN ĐÃ CHÚ Ý BÀI GIẢNG!
Giáo án điện tử toán 7 kết nối tri thức, giáo án powerpoint toán 7 KNTT bài 1: Tập hợp các số hữu tỉ, bài giảng điện tử toán 7 Kết nối
Nâng cấp lên tài khoản VIP để tải tài liệu và dùng thêm được nhiều tiện ích khác
Xem thêm giáo án khác
1. Số hữu tỉ là gì?
HĐ 1. Tính chỉ số WHtR của ông An và ông Chung
Trả lời:
Chỉ số WHtR của ông An là: $\frac{108}{180}$= 0,6
Chỉ số WHtR của ông Chung là: $\frac{70}{160}$ = 0,4375
HĐ2. Ta có thể viết 1,5= $\frac{3}{2}$= $\frac{6}{4}$= $\frac{9}{6}$=....
Tương tự, em hãy viết ba phân số bằng nhau và bằng:
a) - 2,5; b) $2\frac{3}{4}$
Trả lời:
- 2,5= $\frac{5}{2}$= $\frac{10}{4}$= $\frac{15}{6}$=....
$2\frac{3}{4}$ = $\frac{11}{4}$= $\frac{22}{8}$= $\frac{33}{12}$=....
LT1. Giải thích vì sao các số 8; -3,3; $3\frac{2}{3}$đều là các số hữu tỉ. Tìm số đối của mỗi số đó
Trả lời:
Các số 8;−3,3; $3\frac{2}{3}$ đều là các số hữu tỉ vì các số này đều viết được dưới dạng phân số $\frac{a}{b}$ (a,b∈Z,b≠0)
Số đối của các số:
- Số đối của 8 là -8
- Số đối của -3,3 là 3,3
- Số đối của $3\frac{2}{3}$ là $- 3\frac{2}{3}$
LT2. Biểu diễn các số hữu tỉ $\frac{5}{4}$ và $-\frac{5}{4}$ trên trục số.
Trả lời:
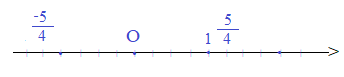
2. Thứ tự trong tập hợp các số hữu tỉ
HĐ3. Viết các số hữu tỉ dưới dạng phân số rồi so sánh:
a. -1,5 và $\frac{5}{2}$ b, - 0,375 và và $-\frac{5}{8}$
Trả lời:
a. $-1,5 = \frac{-15}{10}=\frac{-3}{2}$
Vì -3 < 5 nên $\frac{-3}{2}$ < $\frac{5}{2}$ hay -1,5 < $\frac{5}{2}$
b. Ta có: -0,375 = $\frac{-375}{1000}$ = $\frac{-3}{8}$
Vì 3 < 5 nên -3 > -5, do đó $\frac{-3}{8}$ > $\frac{-5}{8}$ => -0,375 > $\frac{-5}{8}$
HĐ4. Biểu diễn hai số hữu tỉ -1,5 và $\frac{5}{2}$ trên trục số. Em hãy cho biết điểm -1,5 nằm trước hay nằm sau điểm $\frac{5}{2}$ trên trục số.
Trả lời:

Điểm -1,5 nằm trước điểm $\frac{5}{2}$ trên trục số.
LT3. Sắp xếp các số hữu tỉ sau theo thứ tự từ bé đến lớn.
$5\frac{1}{4}$; -2; 3,125; $-\frac{3}{2}$
Trả lời:
Ta có:
$5\frac{1}{4}$ = $\frac{5.4 +1}{4}$ = $\frac{21}{4}$ = $\frac{42}{8}$
- 2 = $-\frac{-16}{8}$
3,125 = $\frac{3125}{1000}$ = $\frac{25}{8}$
$-\frac{3}{2}$ = $-\frac{12}{8}$
Vì -16 < -12 < 25 < 42 nên $-\frac{-16}{8}$ < $-\frac{12}{8}$ < $\frac{25}{8}$ < $\frac{42}{8}$ hay -2 < $-\frac{3}{2}$; 3,125; $5\frac{1}{4}$
