Soạn giáo án điện tử Toán 7 Kết nối bài 7: Luyện tập chung trang 37 (2 tiết)

Nội dung giáo án

CHÀO MỪNG CÁC EM TỚI BÀI HỌC HÔM NAY!

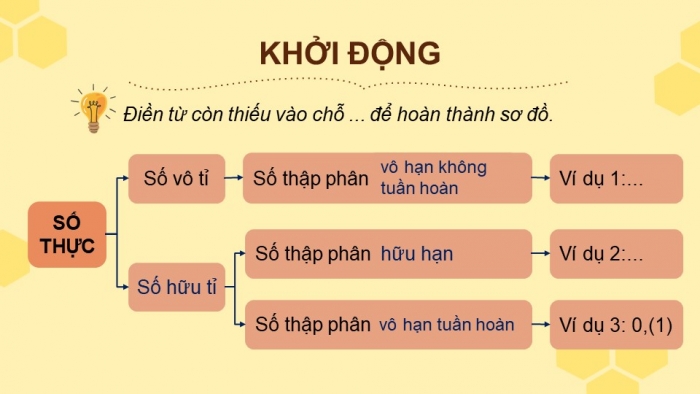
KHỞI ĐỘNG

Điền từ còn thiếu vào chỗ ... để hoàn thành sơ đồ.

LUYỆN TẬP CHUNG (2 Tiết)

Ví dụ 1: Cho hình vuông cạnh 1 cm và hai hình chữ nhật có kích thước 2 cm x 1 cm bằng giấy bìa. Cắt hai hình chữ nhật dọc theo đường chéo để nhận được bốn hình tam giác vuông bằng nhau.

1. Hãy ghép bốn tam giác vuông với hình vuông đã cho để nhận được một hình vuông mới, tính diện tích hình vuông đó.
2. Độ dài đường chéo của hình chữ nhật trên bằng bao nhiêu cm (làm tròn kết quả đến chữ số thập phân thứ hai)?

          Giải

1. a) Ghép bốn tam giác vuông và hình vuông cạnh 1 cm, ta được một hình vuông như hình bên.

Hình vuông cạnh 1 cm có diện tích là: 1. 1 = 1 (cm²)

Diện tích mỗi tam giác vuông là: . 2. 1 = 1 (cm²)

Diện tích hình vuông tạo thành là : 1 + 4. 1 = 5 (cm²)

1. b) Độ dài đường chéo của hình chữ nhật ban đầu cũng bằng cạnh hình vuông tạo thành và bằng 2,24 (cm).

Ví dụ 2

Tính ; ;  (trong đó a là số thực dương cho trước).

Giải

Ta có:  = 3 vì 3 > 0;       = 4,1;         = a

LUYỆN TẬP

Bài 2.19 (SGK - tr38)

Cho bốn phân số: ; ;  và

1. Phân số nào trong những phân số trên không viết được dưới dạng số thập phân hữu hạn?
2. Cho biết = 1,414213562... hãy so sánh phân số tìm được trong câu a) với .

Giải

7. a) Phân số có mẫu số bằng 91 = 13 có ước nguyên tố khác 2 và 5 nên phân số này không viết được dưới dạng số thập phân hữu hạn. Thực hiện phép chia 133 cho 91 ta được kết quả là một số thập phân vô hạn tuần hoàn: =1,(461538);
8. b) 1,414213562…< 1,43 < 1,461538 < 1,(461538) = . Vậy <

Bài 2.20 (SGK - tr38)

1. Viết các phân số sau dưới dạng số thập phân vô hạn tuần hoàn (dùng dấu ngoặc để rõ chu kì): ; . Em có nhận xét gì về kết quả nhận được?
2. Em hãy dự đoán dạng thập phân của .
3. a) = 0,(1); = 0,(01)
4. b) = 0,(001)

Bài 2.21 (SGK - tr38)

Viết  và  dưới dạng số thập phân vô hạn tuần hoàn.

Giải

 = 5.  = 5. 0,(1) = 0,(5)

 = 5.  = 5. 0,(01) = 0,(05)

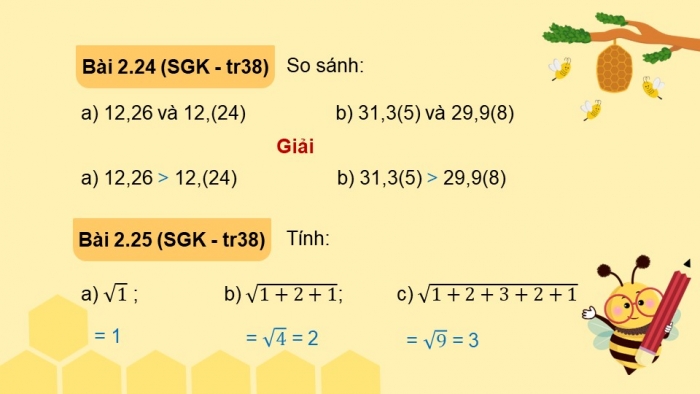
Bài 2.24 (SGK - tr38)

So sánh:

1. a) 12,26 và 12,(24) b) 31,3(5) và 29,9(8)

Giải

1. a) 12,26 > 12,(24) b) 31,3(5) > 29,9(8)

Bài 2.25 (SGK - tr38)

Tính:

1. a) ; b) ;          c)

VẬN DỤNG

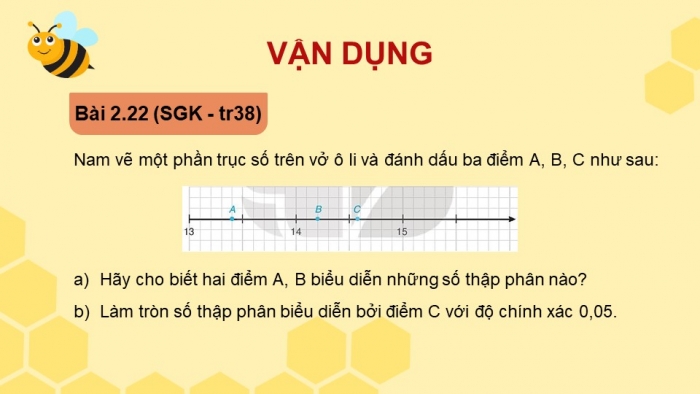
Bài 2.22 (SGK - tr38)

Nam vẽ một phần trục số trên vở ô li và đánh dấu ba điểm A, B, C như sau:

1. Hãy cho biết hai điểm A, B biểu diễn những số thập phân nào?
2. Làm tròn số thập phân biểu diễn bởi điểm C với độ chính xác 0,05.
3. b) Gọi M, N lần lượt là điểm biểu diễn các số 14,5 và 14,6 ; Gọi c là số thập phân được biểu diễn bởi điểm C.

Ta có: làm tròn với độ chính xác 0,05 nghĩa là làm tròn số thập phân đến hàng phần mười.

Từ hình vẽ ta thấy điểm C nằm giữa hai điểm M,N; điểm C gần N hơn, suy ra làm tròn C đến hàng phân mười thì c ≈ 14,6.

Bài 2.23 (SGK - tr38)

Thay dấu “?” bằng chữ số thích hợp:

1. a) -7,02 < -7, (1); b) -15,3       021 < -15,3819

Bài 2.26 (SGK - tr38)

Tính: a)                            b)

Bài 1: Điền dấu        vào ô thích hợp trong các bảng sau:

Bài 2: Điền số thích hợp vào ô trống.

HƯỚNG DẪN VỀ NHÀ

Ghi nhớ các kiến thức đã học

Hoàn thành bài tập trong SBT

Chuẩn bị bài “Ôn tập chương II”

4 nhóm vẽ sơ đồ các kiến thức chương II, chuẩn bị thước dây có vạch chia và một sợi dây dài 10 m.

CẢM ƠN CÁC EM ĐÃ LẮNG NGHE BÀI GIẢNG!