Giải bài tập 7 trang 90 SBT toán 8 tập 1 cánh diều:
Bài tập 7 trang 90 SBT toán 8 tập 1 cánh diều:
Góc kề bù với một góc của tứ giác được gọi là góc ngoài của tứ giác. Chứng minh tổng các góc ngoài của tứ giác ABCD ở Hình 7 (tại mỗi đỉnh chỉ chọn một góc ngoài): $\widehat{A_{1}}+\widehat{B_{1}}+\widehat{C_{1}}+\widehat{D_{1}}$ = 360°.
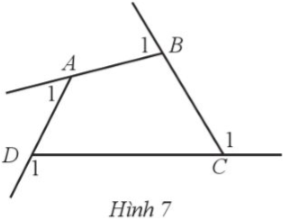
Trong tứ giác ABCD, ta có:
$\widehat{DAB}+\widehat{ABC}+\widehat{BCD}+\widehat{CDA}$ = 360°.
Ta có:
$\widehat{DAB}+\widehat{A_{1}}=\widehat{ABC}+\widehat{B_{1}}=\widehat{BCD}+\widehat{C_{1}}=\widehat{CDA}+\widehat{D_{1}}$ = 180° (các cặp góc kề bù).
=> (180° - $\widehat{A_{1}}$) + (180° - $\widehat{B_{1}}$) + (180° - $\widehat{C_{1}}$) + (180° - $\widehat{D_{1}}$) = 360°
hay 720° – $(\widehat{A_{1}}+\widehat{B_{1}}+\widehat{C_{1}}+\widehat{D_{1}})$ = 360°.
Vậy $\widehat{A_{1}}+\widehat{B_{1}}+\widehat{C_{1}}+\widehat{D_{1}}$ = 360°.
Xem toàn bộ: Giải SBT Toán 8 Cánh diều bài 2 Tứ giác
Giải những bài tập khác
Giải bài tập những môn khác
Giải sgk lớp 8 cánh diều
Giải SBT lớp 8 kết nối tri thức
Giải SBT lớp 8 chân trời sáng tạo
Soạn SBT lớp 8 cánh diều
Trắc nghiệm 8 Kết nối tri thức
Trắc nghiệm 8 Chân trời sáng tạo
Trắc nghiệm 8 Cánh diều
Bộ đề thi, đề kiểm tra lớp 8 chân trời sáng tạo
Giáo án lớp 8
Bình luận