Giải Bài tập 10 trang 21 sgk Toán 11 tập 1 Cánh diều
Bài tập 10 trang 21 sgk Toán 11 tập 1 Cánh diều: Có hai chung cư cao tầng xây cạnh nhau với khoảng cách giữa chúng là HK = 20 m. Để đảm bảo an ninh, trên nóc chung cư thứ hai người ta lắp camera ở vị trí C. Gọi A, B lần lượt là vị trí thấp nhất, cao nhất trên chung cư thứ nhất mà camera có thể quan sát được (Hình 18). Hãy tính số đo góc ACB (phạm vi camera có thể quan sát được ở chung cư thứ nhất). Biết rằng chiều cao của chung cư thứ hai là CK = 32 m, AH = 6 m, BH = 24 m (làm tròn kết quả đến hàng phần mười theo đơn vị độ).

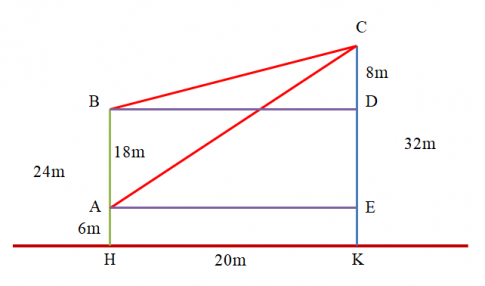
Gọi D, E nằm trên đường thẳng CK sao cho BD, AE $\parallel $ HK.
Từ hình vẽ, ta có: $\widehat{ACB}=\widehat{BCD}-\widehat{ACE}$
Ta có: $tan\widehat{ACB}=tan(\widehat{BCD}-\widehat{ACE})$
Áp dụng công thức $tan(a-b)=\frac{tana-tanb}{1+tanatanb}$
Suy ra: $tan(\widehat{BCD}-\widehat{ACE})= \frac{45}{76}$ nên $tan\widehat{ACB}=\frac{45}{76}$.
Do đó: $\widehat{ACB}=30.63^{\circ}$.
Giải những bài tập khác
Giải bài tập những môn khác
Giải sgk lớp 11 KNTT
Giải sgk lớp 11 CTST
Giải sgk lớp 11 cánh diều
Giải SBT lớp 11 kết nối tri thức
Giải SBT lớp 11 chân trời sáng tạo
Giải SBT lớp 11 cánh diều
Giải chuyên đề học tập lớp 11 kết nối tri thức
Giải chuyên đề toán 11 kết nối tri thức
Giải chuyên đề ngữ văn 11 kết nối tri thức
Giải chuyên đề vật lí 11 kết nối tri thức
Giải chuyên đề hóa học 11 kết nối tri thức
Giải chuyên đề sinh học 11 kết nối tri thức
Giải chuyên đề kinh tế pháp luật 11 kết nối tri thức
Giải chuyên đề lịch sử 11 kết nối tri thức
Giải chuyên đề địa lí 11 kết nối tri thức
Giải chuyên đề mĩ thuật 11 kết nối tri thức
Giải chuyên đề âm nhạc 11 kết nối tri thức
Giải chuyên đề công nghệ chăn nuôi 11 kết nối tri thức
Giải chuyên đề công nghệ cơ khí 11 kết nối tri thức
Giải chuyên đề tin học 11 định hướng Khoa học máy tính kết nối tri thức
Giải chuyên đề tin học 11 định hướng Tin học ứng dụng kết nối tri thức
Giải chuyên đề quốc phòng an ninh 11 kết nối tri thức
Giải chuyên đề hoạt động trải nghiệm hướng nghiệp 11 kết nối tri thức
Giải chuyên đề học tập lớp 11 chân trời sáng tạo
Giải chuyên đề học tập lớp 11 cánh diều
Trắc nghiệm 11 Kết nối tri thức
Trắc nghiệm 11 Chân trời sáng tạo
Trắc nghiệm 11 Cánh diều
Bộ đề thi, đề kiểm tra lớp 11 kết nối tri thức
Đề thi Toán 11 Kết nối tri thức
Đề thi ngữ văn 11 Kết nối tri thức
Đề thi vật lí 11 Kết nối tri thức
Đề thi sinh học 11 Kết nối tri thức
Đề thi hóa học 11 Kết nối tri thức
Đề thi lịch sử 11 Kết nối tri thức
Đề thi địa lí 11 Kết nối tri thức
Đề thi kinh tế pháp luật 11 Kết nối tri thức
Đề thi công nghệ cơ khí 11 Kết nối tri thức
Đề thi công nghệ chăn nuôi 11 Kết nối tri thức
Đề thi tin học ứng dụng 11 Kết nối tri thức
Đề thi khoa học máy tính 11 Kết nối tri thức
Bộ đề thi, đề kiểm tra lớp 11 chân trời sáng tạo
Bộ đề thi, đề kiểm tra lớp 11 cánh diều
Đề thi Toán 11 Cánh diều
Đề thi ngữ văn 11 Cánh diều
Đề thi vật lí 11 Cánh diều
Đề thi sinh học 11 Cánh diều
Đề thi hóa học 11 Cánh diều
Đề thi lịch sử 11 Cánh diều
Đề thi địa lí 11 Cánh diều
Đề thi kinh tế pháp luật 11 Cánh diều
Đề thi công nghệ cơ khí 11 Cánh diều
Đề thi công nghệ chăn nuôi 11 Cánh diều
Đề thi tin học ứng dụng 11 Cánh diều
Đề thi khoa học máy tính 11 Cánh diều

Bình luận