TRẮC NGHIỆM

Câu 1: Cho hàm số . Gọi lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn . Khi đó bằng:

• A. .
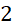• B. .
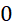• C. .

• D. .

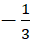Câu 2: Tính tổng giá trị nhỏ nhất và giá trị lớn nhất của hàm số trên đoạn .

• A. .
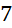• B. .

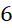• C. .

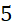• D. .

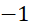Câu 3: Giá trị nhỏ nhất của hàm số trên đoạn là:

• A. 0

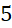
• B. .
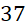• C. .
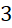• D. .

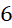Câu 4: Cho hàm số . Hỏi hàm số đồng biến trên khoảng nào dưới đây?

• A. ..

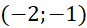• B. .
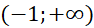• C. .
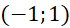• D. .

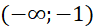Câu 5: Tập hợp tất cả các giá trị thực của tham số để hàm số đạt giá trị cực đại tại là:

• A. .
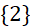• B. .

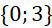• C. .

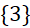• D. .

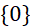Câu 6: Tìm để đồ thị hàm số có điểm cực đại và điểm cực tiểu lập thành tam giác đều.

• A. .
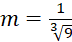• B. .

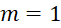• C. .

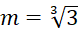• D. .

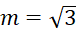Câu 7: Tìm điều kiện của để hàm số có 5 điểm cực trị.

• A. .

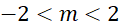• B. .
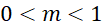• C. .
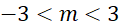• D. .

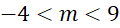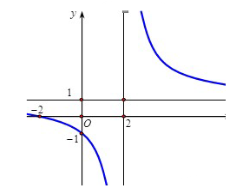
Câu 8: Tìm để hàm số có đồ thị như hình vẽ sau:

• A. .

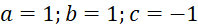• B.

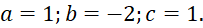
• C. .
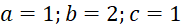• D.

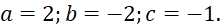
Câu 9: Cho hàm số làm hàm số bậc bốn có bảng biến thiên như hình vẽ.

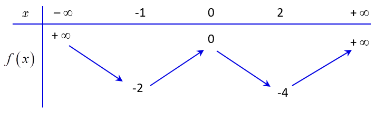
Có bao nhiêu giá trị nguyên của tham số để phương trình có bốn nghiệm thực phân biệt ?

• A. .

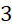• B. .
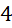• C. .
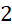• D. .

Câu 10: Ta xác định được các số để đồ thị hàm số đi qua điểm và có điểm cực trị . Tính giá trị biểu thức .

• A.
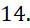
• B. .
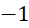• C. .

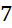• D. .

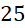Câu 11: Cho hàm số liên tục trên từng khoảng và . Đồ thị hàm số đó cùng với đường tiệm cận đứng và đường tiệm cận ngang như hình vẽ:

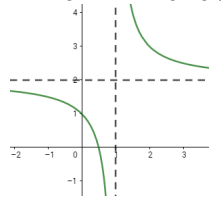
Tìm tất cả các giá trị của tham số để phương trình có hai nghiệm phân biệt sao cho .

• A. .

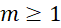• B. .

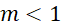• C. .
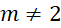• D. .

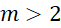Câu 12: Cho hàm số có đồ thị và . Số tiệm cận ngang của là:

• A.
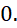
• B.

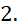
• C.

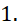
• D. .

Câu 13: Cho là điểm có hoành độ dương thuộc đồ thị hàm số , sao cho tổng khoảng cách từ đến hai đường tiệm cận của đồ thị hàm số là nhỏ nhất. Tọa độ điểm là:

• A.

• B. .
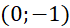• C. .
• D. .

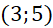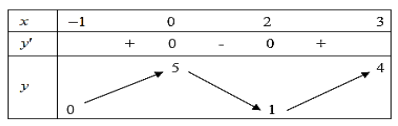
Câu 14: Cho hàm số liên tục và có bảng biến thiên trong đoạn như hình. Gọi là giá trị lớn nhất của hàm số trên đoạn . Tìm mệnh đề đúng?

• A.
• B.
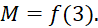
• C.

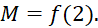
• D. .

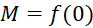Câu 15: Cho hàm số xác định trên, liên tục và có đạo hàm trên khoảng . Xét các mệnh đề sau:

(1) Nếu đồng biến trên thì hàm số không có cực trị trên .

(2) Nếu nghịch biến trên thì hàm số không có cực trị trên .

(3) Nếu đạt cực trị tại điểm thì tiếp tuyến của đồ thị của đồ thị hàm số tại điểm song song hoặc trùng với trục hoành.

(4) Nếu đạt cực đại tại thì đồng biến trên và nghịch biến trên .

Trong các mệnh đề trên, có bao nhiêu mệnh đề đúng?

• A. .

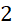• B. .

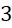• C. .
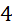• D. .

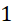Câu 16: Cho hàm số có bảng biến thiêm như hình vẽ bên dưới. Hàm số đã cho đồng biến trên khoảng nào sau đây?

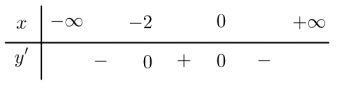
• A.
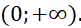
• B.
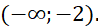
• C.

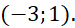
• D. .

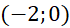Câu 17: Cho hàm số có đạo hàm . Giá trị nhỏ nhất của hàm số trên đoạn bằng:

• A. .

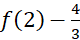• B. .

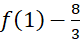• C. .
• D. .

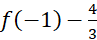Câu 18: Tập hợp tất cả các giá trị thực của tham số để hàm số đồng biến trên từng khoảng xác định là:

• A. .

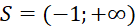• B.
• C. .
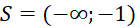• D. .

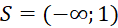Câu 19: Gọi là tập hợp tất cả các giá trị của tham số để hàm số đạt giá trị nhỏ nhất trên bằng . Tính tổng bình phương các phần tử của .

• A. .
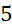• B. .

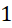• C. .

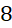• D. .

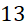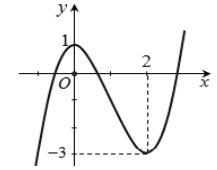
Câu 20: Cho hàm số bậc ba có đồ thị như hình vẽ. Hỏi đồ thị hàm số có bao nhiêu đường tiệm cận đứng?

• A. .
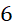• B. .

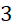• C. .

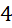• D. .

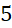Câu 21: Cho là hàm bậc bốn và có bảng biến thiên như hình vẽ:

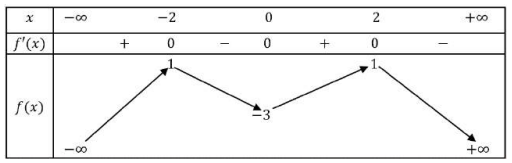
Đồ thị hàm số có mấy đường tiệm cận?

• A. .
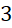• B. .
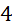• C. .

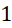• D. .