Đáp án Toán 12 cánh diều Bài tập cuối chương I
Đáp án Bài tập cuối chương I. Bài giải được trình bày ngắn gọn, chính xác giúp các em học Toán 12 cánh diều dễ dàng. Từ đó, hiểu bài và vận dụng vào các bài tập khác. Đáp án chuẩn chỉnh, rõ ý, dễ tiếp thu. Kéo xuống dưới để xem chi tiết
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
BÀI TẬP CUỐI CHƯƠNG I
Bài 1: Cho hàm số ![]() có đạo hàm trên ℝ và hàm số
có đạo hàm trên ℝ và hàm số ![]() có đồ thị như Hình 31.
có đồ thị như Hình 31.
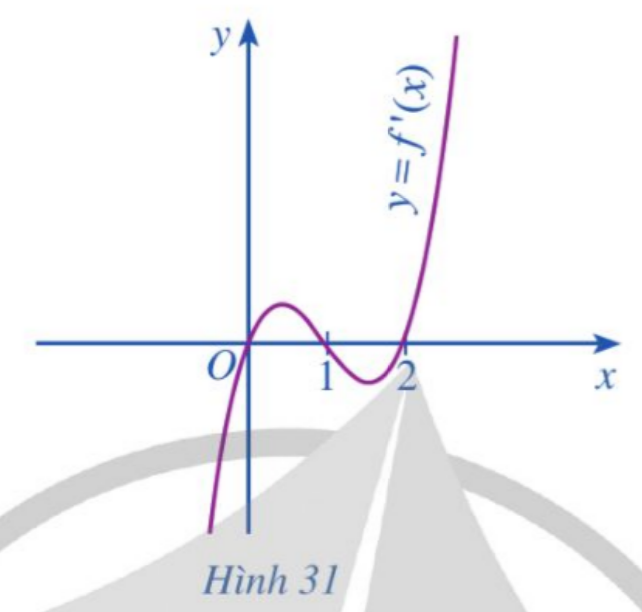
Hàm số ![]() đồng biến trên khoảng:
đồng biến trên khoảng:
Đáp án chuẩn:
A. |
Bài 2: Số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số 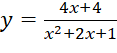 là:
là:
|
|
|
|
Đáp án chuẩn:
C. 2 |
Bài 3: Hàm số nào có đồ thị như Hình 32?
Đáp án chuẩn:
A. |
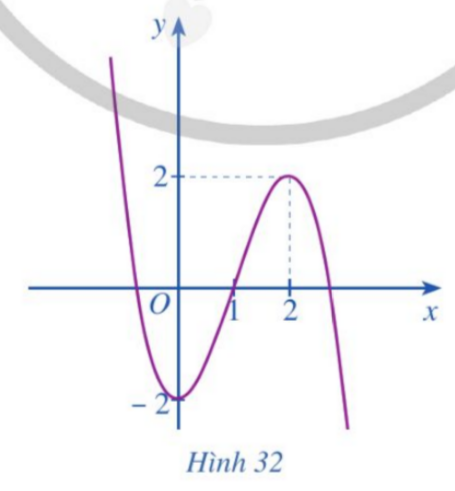
Bài 4: Đường cong ở Hình 33 là đồ thị của hàm số nào sau đâu?
Đáp án chuẩn:
D. 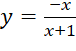
Bài 5: Các đồ thị hàm số ở Hình 34a, Hình 34b đều có đường tiệm cận đứng và đường tiệm cận ngang (hoặc tiệm cận xiên). Hỏi đó là đồ thị của hàm số nào trong các hàm số sau?
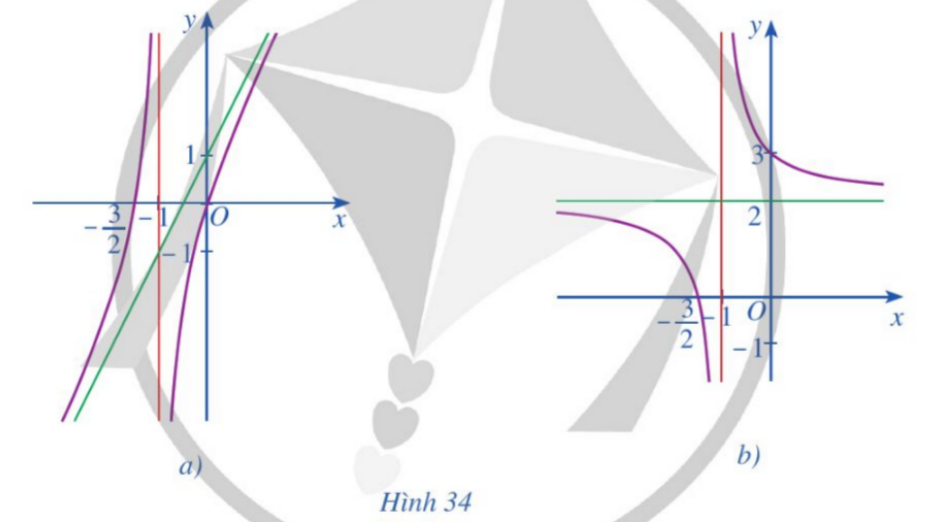
B. | C. |
Đáp án chuẩn:
Đồ thị hàm số ở Hình 34b là đồ thị của hàm số 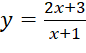
Bài 6: Tìm các đường tiệm cận ngang và tiệm cận đứng của đồ thị mỗi hàm số sau:
b) | c) |
Đáp án chuẩn:
a) Đường thẳng 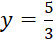 là tiệm cận ngang của đồ thị hàm số
là tiệm cận ngang của đồ thị hàm số
Đường thẳng 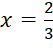 là tiệm cận đứng của đồ thị hàm số
là tiệm cận đứng của đồ thị hàm số
b) Đường thẳng ![]() là tiệm cận ngang của đồ thị hàm số.
là tiệm cận ngang của đồ thị hàm số.
Đường thẳng ![]() là tiệm cận đứng của đồ thị hàm số
là tiệm cận đứng của đồ thị hàm số
c) ![]() và
và ![]() là các tiệm cận ngang của đồ thị hàm số.
là các tiệm cận ngang của đồ thị hàm số.
![]() và
và ![]() là các tiệm cận đứng của đồ thị hàm số
là các tiệm cận đứng của đồ thị hàm số
Bài 7: Tìm các đường tiệm cận đứng và tiệm cận xiên của đồ thị mỗi hàm số sau:
Đáp án chuẩn:
a) ![]() là tiệm cận đứng của đồ thị hàm số
là tiệm cận đứng của đồ thị hàm số
![]() là tiệm cận xiên của đồ thị hàm số
là tiệm cận xiên của đồ thị hàm số
b) ![]() là tiệm cận đứng của đồ thị hàm số
là tiệm cận đứng của đồ thị hàm số
![]() là tiệm cận xiên của đồ thị hàm số
là tiệm cận xiên của đồ thị hàm số
c) 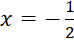 là tiệm cận đứng của đồ thị hàm số
là tiệm cận đứng của đồ thị hàm số
![]() là tiệm cận xiên của đồ thị hàm số
là tiệm cận xiên của đồ thị hàm số
Bài 8: Tìm giá trị nhỏ nhất và giá trị lớn nhất của mỗi hàm số sau:
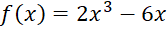 trên đoạn
trên đoạn 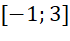 ;
;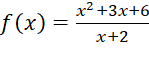 trên đoạn
trên đoạn  ;
;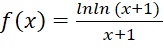 trên đoạn
trên đoạn 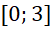 ;
;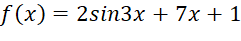 trên đoạn
trên đoạn 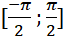 .
.
Đáp án chuẩn:
a) Ta có: ![]() . Khi đó trên khoảng
. Khi đó trên khoảng ![]() ,
, ![]() khi
khi ![]() .
.
![]() ,
, ![]() ,
, ![]() .
.
Như vậy ![]() tại
tại ![]() ,
, ![]() tại
tại ![]() .
.
b) Ta có: 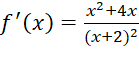 . Khi đó trên khoảng
. Khi đó trên khoảng ![]() , không tồn tại
, không tồn tại ![]() để
để![]() .
.
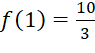 ,
, 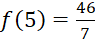 .
.
Như vậy 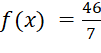 tại
tại ![]() ,
, 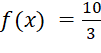 tại
tại ![]() .
.
c) Ta có: 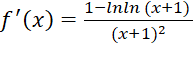 . Khi đó trên khoảng
. Khi đó trên khoảng ![]() ,
, ![]() khi
khi ![]() .
.
![]() ,
, 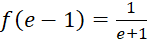 ,
, 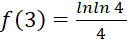 .
.
Như vậy 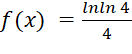 tại
tại ![]() ,
, ![]() tại
tại ![]() .
.
Ta có: ![]() . Khi đó trên khoảng
. Khi đó trên khoảng 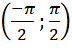 , ta có
, ta có ![]() .
.
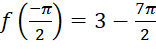 ,
, 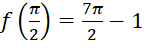
Như vậy 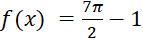 tại
tại  ,
, 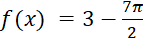 tại
tại 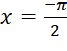
Bài 9: Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
a. | b. |
c. | d. |
e. | f. |
Đáp án chuẩn:
a)
a)
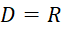 .
.Sự biến thiên:
Giới hạn tại vô cực:
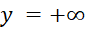 ,
,  .
.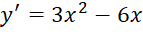 ;
;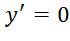 ↔
↔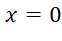 hoặc
hoặc 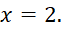
Bảng biến thiên:

Hàm số đã cho đồng biến trên mỗi khoảng ![]() và
và ![]() ; nghịch biến trên khoảng
; nghịch biến trên khoảng ![]() .
.
Hàm số đạt cực đại tại ![]() đạt cực tiểu tại
đạt cực tiểu tại ![]()
3. Đồ thị:
- Giao điểm của đồ thị với trục tung: ![]() .
.
- Giao điểm của đồ thị với trục hoành: ![]() ,
, ![]() .
.
- Đồ thị hàm số đi qua các điểm: ![]() ,
, ![]() ,
, ![]() ,
, ![]() và
và ![]() .
.
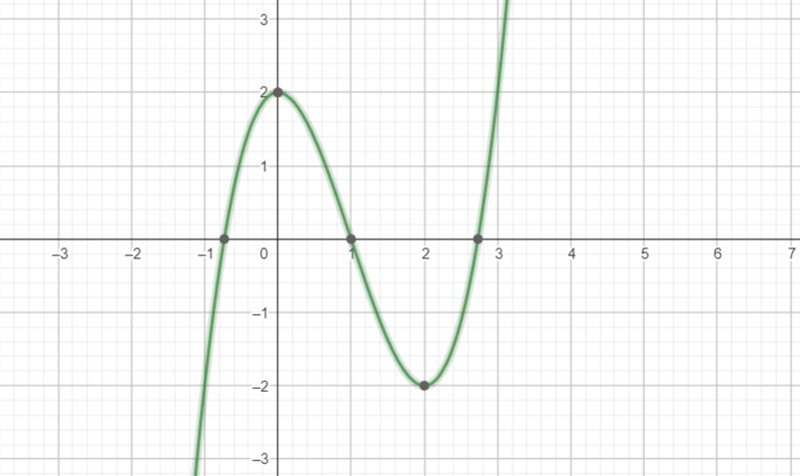
a)
1. ![]()
2. Sự biến thiên:
- Giới hạn tại vô cực: ![]() ,
, ![]()
- ![]() với
với ![]()
- Bảng biến thiên:
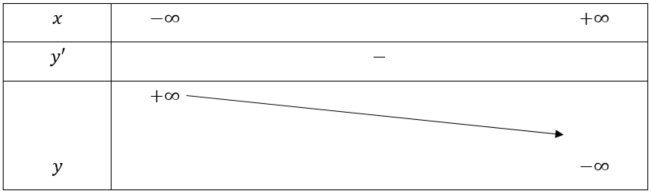
Hàm số đã cho nghịch biến trên khoảng ![]() .
.
Hàm số không có cực trị.
3. Đồ thị:
- Đồ thị hàm số đi qua gốc tọa độ ![]()
- Đồ thị hàm số đi qua các điểm ![]() ,
, ![]() ,
, ![]()
b)
1. ![]()
2. Sự biến thiên:
- Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận:
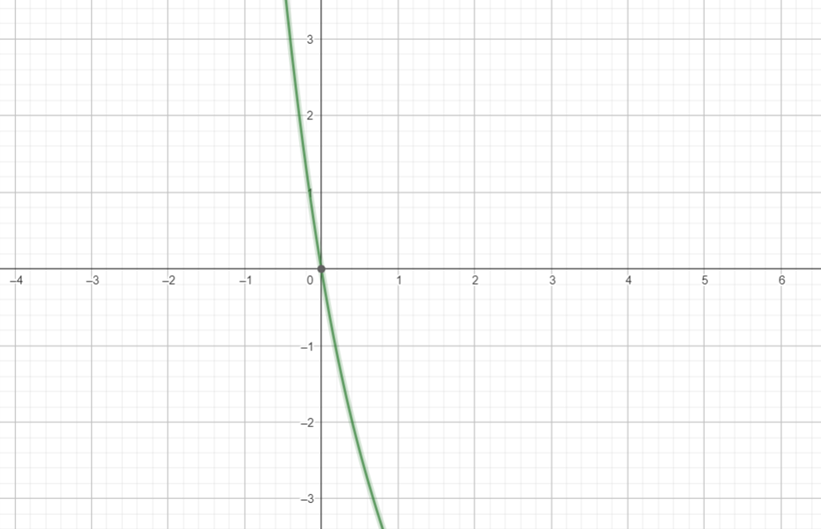
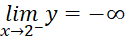 ,
, 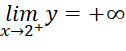
=> ![]() là tiệm cận đứng của đồ thị hàm số.
là tiệm cận đứng của đồ thị hàm số.
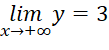 ,
, 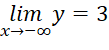
=> ![]() là tiệm cận ngang của đồ thị hàm số.
là tiệm cận ngang của đồ thị hàm số.
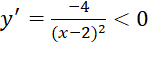 , với
, với ![]() ..
..
Bảng biến thiên:
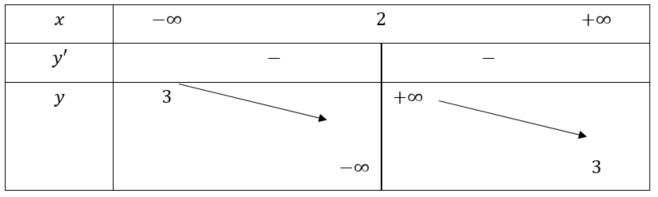
Hàm số đã cho nghịch biến trên mỗi khoảng ![]() và
và ![]() .
.
Hàm số không có cực trị.
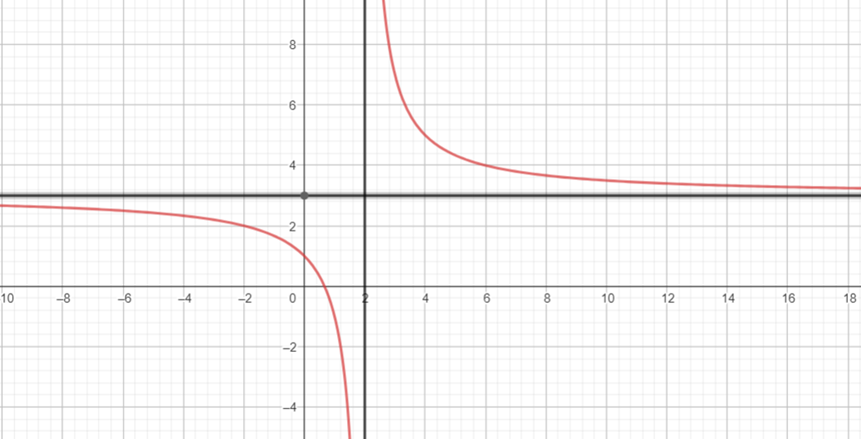
3. Đồ thị:
- Giao điểm của đồ thị với trục tung: ![]() .
.
- Giao điểm của đồ thị với trục hoành: 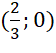 .
.
- Đồ thị hàm số đi qua các điểm: ![]() ,
, ![]() ,
, 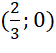 ,
, ![]() và
và ![]() .
.
- Đồ thị hàm số nhận giao điểm ![]() của hai đường tiệm cận của đồ thị làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.
của hai đường tiệm cận của đồ thị làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.
c)
1. 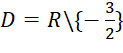
2. Sự biến thiên:
- Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận:
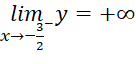 ,
, 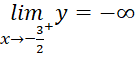
=>  là tiệm cận đứng của đồ thị hàm số
là tiệm cận đứng của đồ thị hàm số
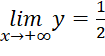 ,
, 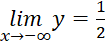
=> 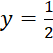 là tiệm cận ngang của đồ thị hàm số
là tiệm cận ngang của đồ thị hàm số
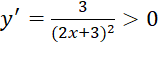 , với
, với ![]() .
.
Bảng biến thiên:
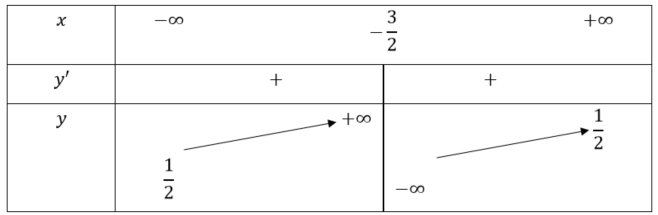
Hàm số đã cho đồng biến trên mỗi khoảng 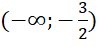 và
và 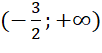 .
.
Hàm số không có cực trị.
3. Đồ thị:
- Đồ thị hàm số đi qua gốc tọa độ ![]() .
.
- Đồ thị hàm số đi qua các điểm ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
- Đồ thị hàm số nhận giao điểm 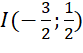 của hai đường tiệm cận của đồ thị làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.
của hai đường tiệm cận của đồ thị làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.

d)
1. ![]()
2. Sự biến thiên:
- Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận:
![]() ,
, ![]() .
.
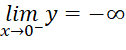 ,
,  .
.
=> ![]() là tiệm cận đứng của đồ thị hàm số.
là tiệm cận đứng của đồ thị hàm số.
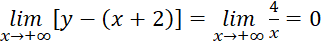 ,
, 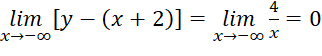 . =>
. => ![]() là tiệm cận xiên của đồ thị hàm số.
là tiệm cận xiên của đồ thị hàm số.
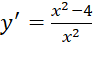 ;
; ![]() ↔
↔ ![]() ↔
↔ ![]() (thỏa mãn) hoặc
(thỏa mãn) hoặc ![]() (thỏa mãn).
(thỏa mãn).
Bảng biến thiên:
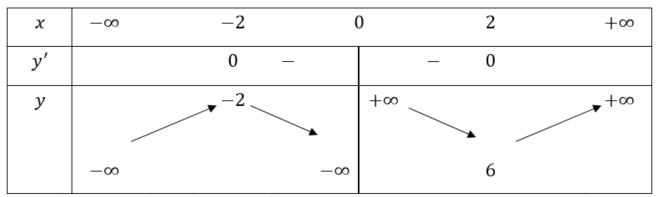
Hàm số đã cho đồng biến trên mỗi khoảng ![]() và
và ![]() ; hàm số đã cho nghịch biến trên mỗi khoảng
; hàm số đã cho nghịch biến trên mỗi khoảng ![]() và
và ![]() .
.
Hàm số đạt cực đại tại ![]() ,
, ![]() ; đạt cực tiểu tại
; đạt cực tiểu tại ![]() ,
, ![]() .
.
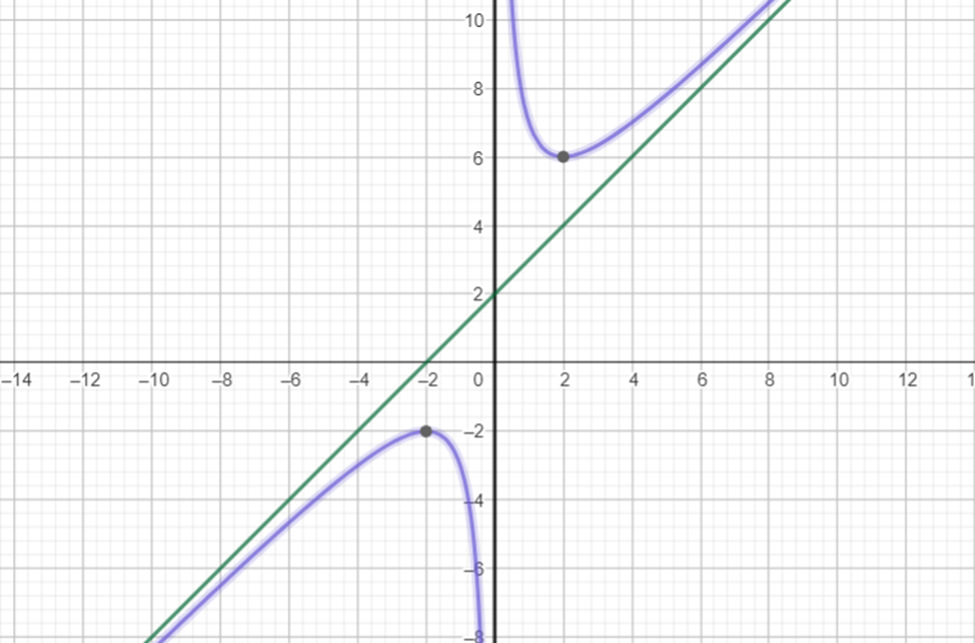
3. Đồ thị:
- Đồ thị hàm số không cắt các trục tọa độ.
- Đồ thị hàm số đi qua các điểm ![]() ,
, ![]() ,
, ![]() và
và ![]() .
.
- Đồ thị hàm số nhận giao điểm ![]() của hai đường tiệm cận của đồ thị làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.
của hai đường tiệm cận của đồ thị làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.
e) 
1. ![]()
2. Sự biến thiên:
- Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận:
![]() ,
, ![]() .
.
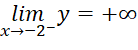 ,
, 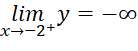 . Do đó, đường thẳng
. Do đó, đường thẳng ![]() là tiệm cận đứng của đồ thị hàm số.
là tiệm cận đứng của đồ thị hàm số.
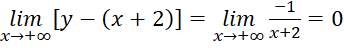 ,
, 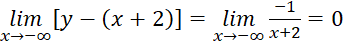 . Do đó, đường thẳng
. Do đó, đường thẳng ![]() là tiệm cận xiên của đồ thị hàm số.
là tiệm cận xiên của đồ thị hàm số.
- 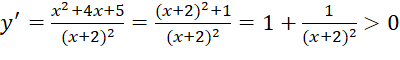 với
với ![]() .
.
Bảng biến thiên:
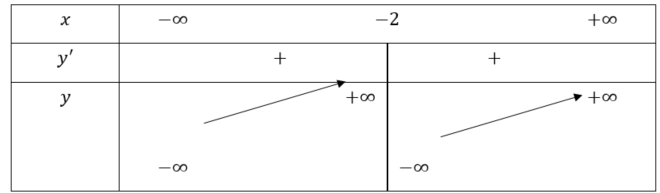
Hàm số đã cho đồng biến trên mỗi khoảng ![]() và
và ![]() .
.
Hàm số không có cực trị.
3. Đồ thị:
- Giao điểm của đồ thị với trục tung: 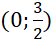 .
.
- Giao điểm của đồ thị với trục hoành: ![]() ,
, ![]() .
.
- Đồ thị hàm số đi qua các điểm: 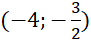 ,
, 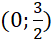 ,
, ![]() và
và ![]() .
.
- Đồ thị hàm số nhận giao điểm ![]() của hai đường tiệm cận của đồ thị làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.
của hai đường tiệm cận của đồ thị làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.
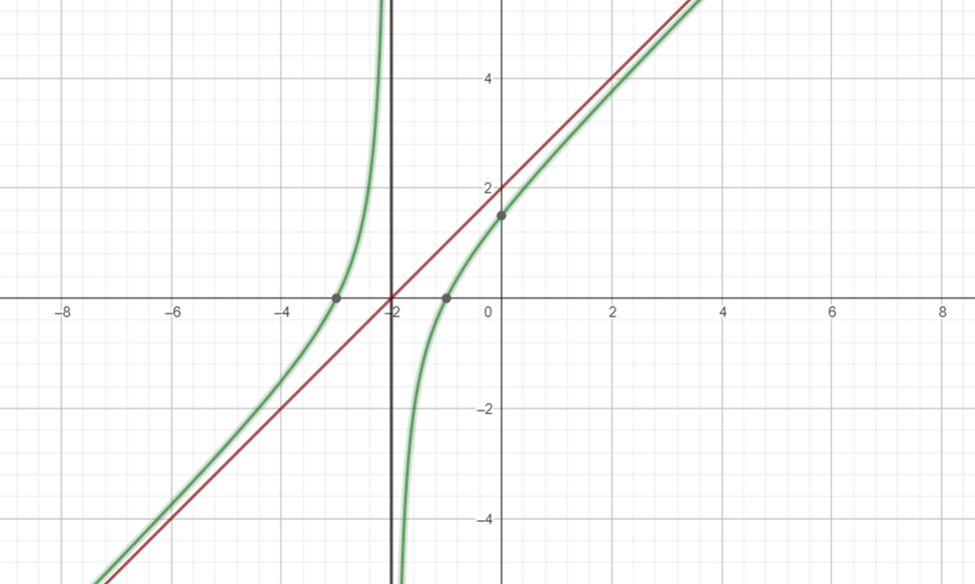
Bài 10: Một trang sách có dạng hình chữ nhật với diện tích là 384 cm2. Sau khi để lề trên và lề dưới đều là 3 cm, để lề trái và lề phải đều là 2 cm. Phần còn lại của trang sách được in chữ. Kích thước tối ưu của trang sách là bao nhiêu để phần in chữ trên trang sách có diện tích lớn nhất?
Đáp án chuẩn:
Gọi ![]() (cm) là chiều rộng của trang sách.
(cm) là chiều rộng của trang sách.
Khi đó, chiều dài của trang sách là ![]() (cm).
(cm).
Sau khi để lề thì phần in chữ có dạng hình chữ nhật có chiều rộng là ![]() (cm) và chiều dài là
(cm) và chiều dài là 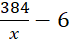 (cm).
(cm).
Rõ ràng, ![]() phải thỏa mãn điều kiện
phải thỏa mãn điều kiện ![]() .
.
Diện tích phần in chữ trên trang sách là:
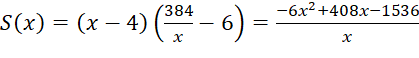 (cm2)
(cm2)
Xét hàm số 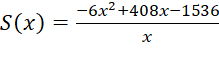 với
với ![]() .
.
Ta có:  ↔
↔ ![]() (không thỏa mãn) hoặc
(không thỏa mãn) hoặc ![]() (thỏa mãn)
(thỏa mãn)
Ta có bảng biến thiên:
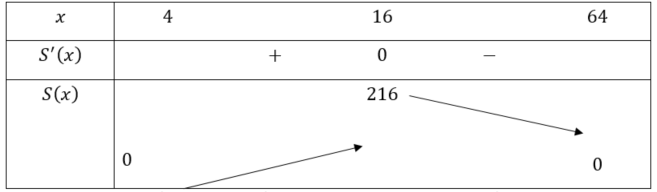
Căn cứ vào bảng biến thiên, ta thấy trên khoảng ![]() , hàm số
, hàm số ![]() đạt giá trị lớn nhất bằng 216 tại
đạt giá trị lớn nhất bằng 216 tại ![]() . Khi đó,
. Khi đó,  .
.
Vậy kích thước tối ưu của trang sách là ![]() (cm) thì in chữ trên trang sách có diện tích lớn nhất.
(cm) thì in chữ trên trang sách có diện tích lớn nhất.
Bài 11: Một người nông dân có 15 000 000 đồng để làm một hàng rào hình chữ E dọc theo một con sông bao quanh hai khu đất trồng rau có dạng hai hình chữ nhật bằng nhau (Hình 35). Đối với mặt hàng rào song song với bờ sông thì chi phí nguyên vật liệu là 60 000 đồng/mét, còn đối với ba mặt hàng rào song song nhau thì chi phí nguyên vật liệu là 50 000 đồng/mét, mặt giáp với bờ sông không phải rào. Tìm diện tích lớn nhất của hai khu đất thu được sau khi làm hàng rào.
Đáp án chuẩn:
Giả sử chiều dài từng mặt của ba mặt hàng rào song song nhau là ![]() (m).
(m).
Chi phí để làm ba mặt hàng rào song song là: ![]() (đồng).
(đồng).
Chi phí để làm mặt hàng rào song song với bờ sông là: ![]() (đồng).
(đồng).
Chiều dài của mặt hàng rào song song với bờ sông là: 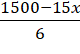 (m)
(m)
Rõ ràng, ![]() phải thỏa mãn điều kiện
phải thỏa mãn điều kiện ![]()
Giả sử diện tích hàng rào không đáng kể, khi đó diện tích hai khu đất thu được sau khi làm hàng rào là: 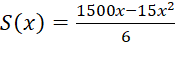 (m2)
(m2)
Xét hàm số 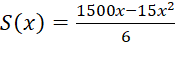 với
với ![]()
Ta có: 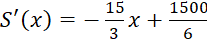
Trên khoảng ![]() ,
, ![]() khi
khi ![]() .
.
Ta có bảng biến thiên:
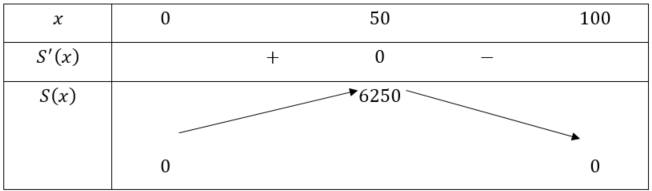
Căn cứ vào bảng biến thiên, ta thấy: Trên khoảng ![]() , hàm số
, hàm số ![]() đạt giá trị lớn nhất bằng 6250 tại
đạt giá trị lớn nhất bằng 6250 tại ![]() .
.
Như vậy diện tích lớn nhất của hai khu đất thu được sau khi làm hàng rào là 6250 m2
Bài 12: Một bác nông dân có ba tấm lưới thép B40, mỗi tấm dài ![]() (m) và muốn rào một mảnh vườn dọc bờ sông có dạng hình thang cân
(m) và muốn rào một mảnh vườn dọc bờ sông có dạng hình thang cân ![]() như Hình 36 (bờ sông là đường thẳng
như Hình 36 (bờ sông là đường thẳng ![]() không phải rào). Hỏi bác đó có thể rào được mảnh vườn có diện tích lớn nhất là bao nhiêu mét vuông?
không phải rào). Hỏi bác đó có thể rào được mảnh vườn có diện tích lớn nhất là bao nhiêu mét vuông?
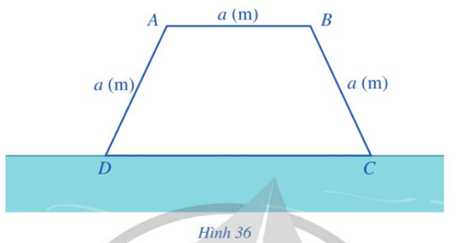
Đáp án chuẩn:

Dựng các đường cao ![]() và
và ![]() của hình thang cân
của hình thang cân ![]() như hình vẽ trên.
như hình vẽ trên.
Vì ![]() là hình than cân nên
là hình than cân nên ![]() và
và ![]() .
.
Đặt ![]() (m) (
(m) (![]() )
)
Ta có: ![]()
Theo định lý Pythagore => ![]() (m).
(m).
Rõ ràng, ![]() phải thỏa mãn điều kiện
phải thỏa mãn điều kiện ![]() .
.
Diện tích của hình thang cân ![]() là:
là:
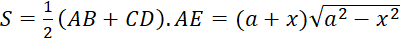 (m2)
(m2)
Xét hàm số ![]() với
với ![]()
Ta có:  ;
;
![]()
↔ ![]() (không thỏa mãn) hoặc
(không thỏa mãn) hoặc 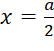 (thỏa mãn).
(thỏa mãn).
Bảng biến thiên:
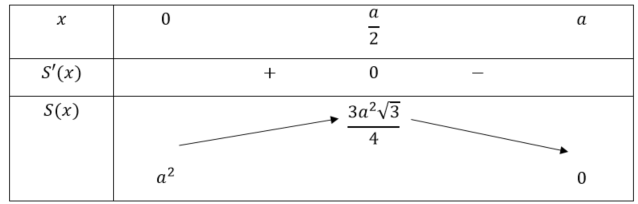
Căn cứ vào bảng biến thiên, ta thấy hàm số ![]() đạt giá trị lớn nhất bằng
đạt giá trị lớn nhất bằng 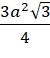 tại
tại 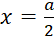 .
.
Vậy bác đó có thể rào được mảnh vườn có diện tích lớn nhất là 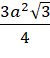 (m2)
(m2)
Bài 13: Có hai xã cùng ở một bên bờ sông Lam. Người ta đo được khoảng cách từ trung tâm ![]() ,
, ![]() của hai xã đó đến bờ sông lần lượt là
của hai xã đó đến bờ sông lần lượt là ![]() m,
m, ![]() m và
m và ![]() m (Hình 37). Các kỹ sư muốn xây một trạm cung cấp nước sạch nằm bên bờ sông Lam cho người dân hai xã. Để tiết kiệm chi phí, các kĩ sư cần phải chọn vị trí
m (Hình 37). Các kỹ sư muốn xây một trạm cung cấp nước sạch nằm bên bờ sông Lam cho người dân hai xã. Để tiết kiệm chi phí, các kĩ sư cần phải chọn vị trí ![]() của trạm cung cấp nước sạch đó trên đoạn
của trạm cung cấp nước sạch đó trên đoạn ![]() sao cho tổng khoảng cách từ hai vị trí
sao cho tổng khoảng cách từ hai vị trí ![]() ,
, ![]() đến vị trí
đến vị trí ![]() là nhỏ nhất. Hãy tìm giá trị nhỏ nhất của tổng khoảng cách đó.
là nhỏ nhất. Hãy tìm giá trị nhỏ nhất của tổng khoảng cách đó.

Đáp án chuẩn:
Đặt ![]() (m).
(m).
=> ![]() (m)
(m)
Rõ ràng, ![]() phải thỏa mãn điều kiện
phải thỏa mãn điều kiện ![]() .
.
Áp dụng định lý Pythagore, ta tính được:
![]() (m);
(m);
![]() (m).
(m).
Tổng khoảng cách từ hai vị trí ![]() ,
, ![]() đến vị trí
đến vị trí ![]() là:
là:
![]() với
với ![]() .
.
Ta có: 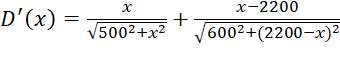 ;
;
Trên khoảng ![]() , ta thấy
, ta thấy ![]() khi
khi ![]() .
.
Bảng biến thiên:
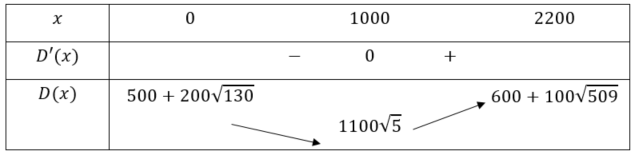
Căn cứ vào bảng biến thiên, ta thấy ![]() đạt giá trị lớn nhất bằng
đạt giá trị lớn nhất bằng ![]() tại
tại ![]() . Vậy giá trị nhỏ nhất của tổng khoảng cách cần tìm là
. Vậy giá trị nhỏ nhất của tổng khoảng cách cần tìm là ![]() m
m
Bài 14: Một công ty kinh doanh bất động sản có 20 căn hộ cho thuê. Biết rằng nếu cho thuê mỗi căn hộ với giá 2 triệu đồng/tháng thì tất cả các căn hộ đều có người thuê. Nhưng cứ mỗi lần tăng giá cho thuê mỗi căn hộ thêm 200 nghìn đồng/tháng thì có thêm một căn hộ bị bỏ trống. Hỏi công ty nên cho thuê mỗi căn hộ bao nhiêu tiền một tháng để tổng số tiền thu được là lớn nhất?
Đáp án chuẩn:
Cứ tăng thêm 200 nghìn đồng vào giá thuê một căn hộ trên một tháng thì có một căn hộ bỏ trống. Gọi số lần tăng 200 nghìn đồng vào gái thuê một căn hộ trên một tháng là ![]() (
(![]() ).
).
Khi đó, ![]() cũng là số căn hộ bị bỏ trống.
cũng là số căn hộ bị bỏ trống.
Tổng số tiền công ty thu được lúc này là: ![]() (nghìn đồng)
(nghìn đồng)
Xét hàm số ![]() với
với ![]() .
.
Ta có: ![]() ;
; ![]() ↔
↔ ![]()
Bảng biến thiên:
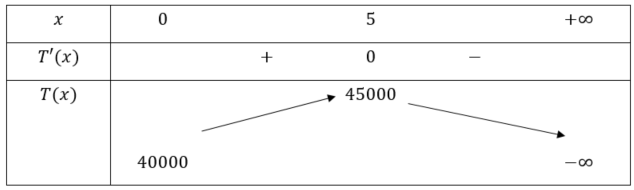
Căn cứ vào bảng biến thiên trên, ta thấy hàm số ![]() đạt giá trị lớn nhất bằng 45000 khi
đạt giá trị lớn nhất bằng 45000 khi ![]() . Khi đó, số tiền tăng lên khi cho thuê một căn hộ là
. Khi đó, số tiền tăng lên khi cho thuê một căn hộ là ![]() nghìn đồng
nghìn đồng ![]() 1 triệu đồng.
1 triệu đồng.
Vậy công ty nên cho thuê mỗi căn hộ 3 triệu đồng/tháng thì tổng số tiền thu được là lớn nhất
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
Nội dung quan tâm khác
Thêm kiến thức môn học
Giải bài tập những môn khác
Môn học lớp 12 KNTT
5 phút giải toán 12 KNTT
5 phút soạn bài văn 12 KNTT
Văn mẫu 12 KNTT
5 phút giải vật lí 12 KNTT
5 phút giải hoá học 12 KNTT
5 phút giải sinh học 12 KNTT
5 phút giải KTPL 12 KNTT
5 phút giải lịch sử 12 KNTT
5 phút giải địa lí 12 KNTT
5 phút giải CN lâm nghiệp 12 KNTT
5 phút giải CN điện - điện tử 12 KNTT
5 phút giải THUD12 KNTT
5 phút giải KHMT12 KNTT
5 phút giải HĐTN 12 KNTT
5 phút giải ANQP 12 KNTT
Môn học lớp 12 CTST
5 phút giải toán 12 CTST
5 phút soạn bài văn 12 CTST
Văn mẫu 12 CTST
5 phút giải vật lí 12 CTST
5 phút giải hoá học 12 CTST
5 phút giải sinh học 12 CTST
5 phút giải KTPL 12 CTST
5 phút giải lịch sử 12 CTST
5 phút giải địa lí 12 CTST
5 phút giải THUD 12 CTST
5 phút giải KHMT 12 CTST
5 phút giải HĐTN 12 bản 1 CTST
5 phút giải HĐTN 12 bản 2 CTST
Môn học lớp 12 cánh diều
5 phút giải toán 12 CD
5 phút soạn bài văn 12 CD
Văn mẫu 12 CD
5 phút giải vật lí 12 CD
5 phút giải hoá học 12 CD
5 phút giải sinh học 12 CD
5 phút giải KTPL 12 CD
5 phút giải lịch sử 12 CD
5 phút giải địa lí 12 CD
5 phút giải CN lâm nghiệp 12 CD
5 phút giải CN điện - điện tử 12 CD
5 phút giải THUD 12 CD
5 phút giải KHMT 12 CD
5 phút giải HĐTN 12 CD
5 phút giải ANQP 12 CD
Giải chuyên đề học tập lớp 12 kết nối tri thức
Giải chuyên đề Ngữ văn 12 Kết nối tri thức
Giải chuyên đề Toán 12 Kết nối tri thức
Giải chuyên đề Vật lí 12 Kết nối tri thức
Giải chuyên đề Hóa học 12 Kết nối tri thức
Giải chuyên đề Sinh học 12 Kết nối tri thức
Giải chuyên đề Kinh tế pháp luật 12 Kết nối tri thức
Giải chuyên đề Lịch sử 12 Kết nối tri thức
Giải chuyên đề Địa lí 12 Kết nối tri thức
Giải chuyên đề Tin học ứng dụng 12 Kết nối tri thức
Giải chuyên đề Khoa học máy tính 12 Kết nối tri thức
Giải chuyên đề Công nghệ 12 Điện - điện tử Kết nối tri thức
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Kết nối tri thức
Giải chuyên đề học tập lớp 12 chân trời sáng tạo
Giải chuyên đề Ngữ văn 12 Chân trời sáng tạo
Giải chuyên đề Toán 12 Chân trời sáng tạo
Giải chuyên đề Vật lí 12 Chân trời sáng tạo
Giải chuyên đề Hóa học 12 Chân trời sáng tạo
Giải chuyên đề Sinh học 12 Chân trời sáng tạo
Giải chuyên đề Kinh tế pháp luật 12 Chân trời sáng tạo
Giải chuyên đề Lịch sử 12 Chân trời sáng tạo
Giải chuyên đề Địa lí 12 Chân trời sáng tạo
Giải chuyên đề Tin học ứng dụng 12 Chân trời sáng tạo
Giải chuyên đề Khoa học máy tính 12 Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Điện - điện tử Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Chân trời sáng tạo
Giải chuyên đề học tập lớp 12 cánh diều
Giải chuyên đề Ngữ văn 12 Cánh diều
Giải chuyên đề Toán 12 Cánh diều
Giải chuyên đề Vật lí 12 Cánh diều
Giải chuyên đề Hóa học 12 Cánh diều
Giải chuyên đề Sinh học 12 Cánh diều
Giải chuyên đề Kinh tế pháp luật 12 Cánh diều
Giải chuyên đề Lịch sử 12 Cánh diều
Giải chuyên đề Địa lí 12 Cánh diều
Giải chuyên đề Tin học ứng dụng 12 Cánh diều
Giải chuyên đề Khoa học máy tính 12 Cánh diều
Giải chuyên đề Công nghệ 12 Điện - điện tử Cánh diều
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Cánh diều

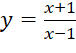
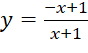
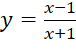
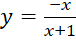
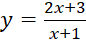
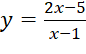

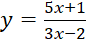
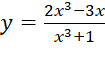
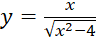

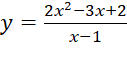
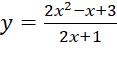
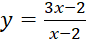
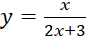

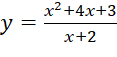
Bình luận